

Nguyễn Vũ Hà Ngân
Giới thiệu về bản thân



































Ta có: \(\frac{x - a}{b c} + \frac{x - b}{c a} + \frac{x - c}{a b} = \frac{2}{a} + \frac{2}{b} + \frac{2}{c}\)
\(\left(\right. \frac{x - a}{b c} - \frac{2}{a} \left.\right) + \left(\right. \frac{x - b}{c a} - \frac{2}{b} \left.\right) + \left(\right. \frac{x - c}{a b} - \frac{2}{c} \left.\right) = 0\)
\(\frac{a \left(\right. x - a \left.\right) - 2 b c + b \left(\right. x - b \left.\right) - 2 c a + c \left(\right. x - c \left.\right) - 2 a b}{a b c} = 0\)
Điều kiện xác định: \(a , b , c \neq 0\)
Khi đó: \(\frac{\left(\right. a + b + c \left.\right) x - a^{2} - 2 b c - b^{2} - 2 c a - c^{2} - 2 a b}{a b c} = 0\)
\(\left(\right. a + b + c \left.\right) x = \left(\left(\right. a + b + c \left.\right)\right)^{2}\)
+ Nếu \(a + b + c = 0\) thì phương trình có vô số nghiệm.
+ Nếu \(a + b + c \neq 0\) thì phương trình có nghiệm duy nhất \(x = a + b + c\)
Ta có: \(\frac{x - a}{b c} + \frac{x - b}{c a} + \frac{x - c}{a b} = \frac{2}{a} + \frac{2}{b} + \frac{2}{c}\)
\(\left(\right. \frac{x - a}{b c} - \frac{2}{a} \left.\right) + \left(\right. \frac{x - b}{c a} - \frac{2}{b} \left.\right) + \left(\right. \frac{x - c}{a b} - \frac{2}{c} \left.\right) = 0\)
\(\frac{a \left(\right. x - a \left.\right) - 2 b c + b \left(\right. x - b \left.\right) - 2 c a + c \left(\right. x - c \left.\right) - 2 a b}{a b c} = 0\)
Điều kiện xác định: \(a , b , c \neq 0\)
Khi đó: \(\frac{\left(\right. a + b + c \left.\right) x - a^{2} - 2 b c - b^{2} - 2 c a - c^{2} - 2 a b}{a b c} = 0\)
\(\left(\right. a + b + c \left.\right) x = \left(\left(\right. a + b + c \left.\right)\right)^{2}\)
+ Nếu \(a + b + c = 0\) thì phương trình có vô số nghiệm.
+ Nếu \(a + b + c \neq 0\) thì phương trình có nghiệm duy nhất \(x = a + b + c\)
a) Với \(m = - 1\), hàm số trở thành \(y = - 2 x + 1\).
Xét hàm số \(y = - 2 x + 1\) :
Thay \(x = 0\) thì \(y = 1\).
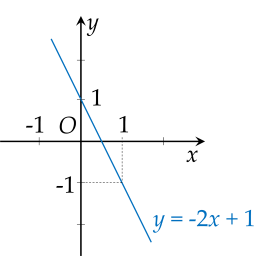
Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 0 ; 1 \left.\right)\).
Thay \(x = 1\) thì \(y = - 1\).
Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 1 \left.\right)\).
Vẽ đồ thị:
b) Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) song song với đường thẳng \(\left(\right. d^{'} \&\text{nbsp}; \left.\right) : y = - 3 x + 9\) nên: \(a \neq - 3 ; b \neq 9\).
Khi đó ta có: \(\left(\right. d \left.\right) : y = - 3 x + b\) và \(b \neq 9\).
Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) đi qua \(A \left(\right. 1 ; - 8 \left.\right)\) nên: \(- 8 = - 3.1 + b\)
Suy ra \(b = - 5\) (thoả mãn)
Vậy đường thẳng cần tìm là \(\left(\right. d \left.\right) : y = - 3 x - 5\)
a) Với \(m = - 1\), hàm số trở thành \(y = - 2 x + 1\).
Xét hàm số \(y = - 2 x + 1\) :
Thay \(x = 0\) thì \(y = 1\).
Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 0 ; 1 \left.\right)\).
Thay \(x = 1\) thì \(y = - 1\).
Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 1 \left.\right)\).
Vẽ đồ thị:

b) Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) song song với đường thẳng \(\left(\right. d^{'} \&\text{nbsp}; \left.\right) : y = - 3 x + 9\) nên: \(a \neq - 3 ; b \neq 9\).
Khi đó ta có: \(\left(\right. d \left.\right) : y = - 3 x + b\) và \(b \neq 9\).
Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) đi qua \(A \left(\right. 1 ; - 8 \left.\right)\) nên: \(- 8 = - 3.1 + b\)
Suy ra \(b = - 5\) (thoả mãn)
Vậy đường thẳng cần tìm là \(\left(\right. d \left.\right) : y = - 3 x - 5\)
a) \(3 x - 5 = 4\)
\(3 x = 9\)
\(x = 3\)
Vậy phương trình có nghiệm \(x = 3\).
b) \(\frac{2 x}{3} + \frac{3 x - 1}{6} = \frac{x}{2}\)
\(\frac{4 x}{6} + \frac{3 x - 1}{6} = \frac{3 x}{6}\)
\(4 x + 3 x - 1 = 3 x\)
\(4 x = 1\)
\(x = \frac{1}{4}\)
Vậy phương trình có nghiệm \(x = \frac{1}{4}\)