HB = 2,126837727

HC = 4,601473629

AH = 4

AC = 5,300051973

 BC = 3,9 cm và góc BAC=78 độ,góc BCA=42 độ

 AB ≈ 2,79 cm, AC ≈ 3,76 cm và góc A= 75 độ

GÓC A = 70 ĐỘ

AC = 3,59 cm; BC= 3,72 cm

a) $\Delta BKC\backsim \Delta DHC$ (g. g)

Vì K^=H^=90∘K=H=90∘ 

D^=B^D=B (cùng bằng A^A)

KCHC=BCDCHCKC​=DCBC​ hay KCHC=BCABHCKC​=ABBC​ (*)

Xét tứ giác $AKCH$ có: A^+HCK^=180∘A+HCK=180∘;

A^+ABC^=180∘A+ABC=180∘

Suy ra: ABC^=HCK^ABC=HCK (**)

Từ (*) và (**) suy ra: $\Delta CKH\backsim \Delta BCA$ (c-g-c)

b) $\Delta CKH\backsim \Delta BCA$ suy ra HKAC=CKBCACHK​=BCCK​

HK=AC.CKBC=AC.sin⁡KBC^HK=AC.BCCK​=AC.sinKBC mà BAD^=KBC^BAD=KBC (cặp góc đồng vị) nên HK=AC.sin⁡BAD^HK=AC.sinBAD.

Nối $B$ và $C$. Kẻ $CH\perp AB$ ($H\in AB$).

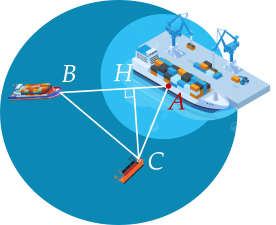
Sau $1,5$ giờ tàu $B$ chạy được quãng đường là: $AB=20.1,5=30$ (hải lí).

Sau $1,5$ giờ tàu $C$ chạy được quãng đường là: $AC=15.1,5=22,5$ (hải lí).

Xét tam giác $AHC$ vuông tại $H$, ta có:

CH=AC.sin⁡A=22,5.sin⁡60∘ =4534CH=AC.sinA=22,5.sin60∘ =4453​​ (hải lí).

AH=AC.cos⁡A=22,5.cos⁡60∘=11,25AH=AC.cosA=22,5.cos60∘=11,25 (hải lí).

Do đó $BH=AB-AH=30-11,25=18,75$ (hải lí).

Mặt khác, tam giác $CHB$ vuông tại $H$, áp dụng định lí Pythagore ta có:

BC=BH2+CH2=(18,75)2+(4534)2≈27,04BC=BH2+CH2​=(18,75)2+(4453​​)2​≈27,04 (hải lí).

Vậy sau $1,5$ giờ tàu $B$ cách tàu $C$ là $27,04$ hải lí.

Gọi x,y$x,y$(đồng) lần lượt là giá niêm yết của mỗi mặt hàng $A$ và $B$ $(x>0,y>0)$

Một khách hàng mua hai món hàng $A$ và một món hàng $B$ hết tổng số tiền là $362000$ đồng nên ta có:

80%x.2+85%y=362000(1)

Trong khung giờ vàng khách hàng mua ba món hàng $A$ và hai món hàng $B$ hết tổng sô tiền là $552000$ đồng nên ta có:

$70\%x.3+75\%y.2=552000$ (2)

Từ (1) và (2) =>

 {1,6x+0,85y=3620002,1x+1,5y=552000
​1,6x+0,85y=3620002,1x+1,5y=552000​

Giải hệ phương trình ta được

{x=120000y=200000
x=120000y=200000​
 

a)  (2x+1)\(^2\) - 9x\(^2\) = 0

(2x+1)\(^2\) - (3x)\(^2\) = 0

(2x+1-3x).(2x+1+3x) = 0

(-x+1).(5x+1)=0

\(\left[{}\begin{matrix}-x+1=0\\5x+1=0\end{matrix}\right.\)=>\(\left[{}\begin{matrix}-x=-1\\5x=-1\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{-1}{5}\end{matrix}\right.\)

b) \(\left\{{}\begin{matrix}5x-4y=3\\2x+y=4\end{matrix}\right.\)   ​

    \(\left\{{}\begin{matrix}5x-4y=3\\\left(2x+y\right).4=4.4\end{matrix}\right.\)

\(\left\{{}\begin{matrix}5x-4y=3\\8x+4y=16\end{matrix}\right.\)

đặt 5x-4y=3 là(1)

     8x +4y=16 là (2)

lấy (1)+(2) ta được

(5x-4y)+(8x+4y)=3+16

13x=19

x=\(\dfrac{19}{13}\)

từ (1) => 4y=5x-3=5.\(\dfrac{19}{13}\)-3=\(\dfrac{56}{13}\)

=>y=\(\dfrac{14}{13}\)

gọi tốc độc của ca nô khi nước yên lặng là x(km/h),x>6

suy ra tốc độ của ca nô khi xuôi dòng là x+6(km/h)

đổi 2 giờ 30 phút=2,5 giờ

suy ra quãng đường ca nô đi được trong thời gian trên là: 

2,5.(x+6) (km)

theo bài ra ta có:

x "<" hoặc "=" 40

=> x+6 "<" hoặc "=" 46

=> 2,5.(x+6) "<" hoặc "=" 115

vậy quãng đường ca nô đi được không quá 115(km)