1. (Không yêu cầu vẽ hình thật chính xác từng cm).

Do A là trung điểm \(� �\), nên \(� � = 2. � �\).

Thay số \(� � = 2\) cm, ta có

\(� � = 2.2 = 4\) (cm)

2. (Không yêu cầu vẽ lại hình).

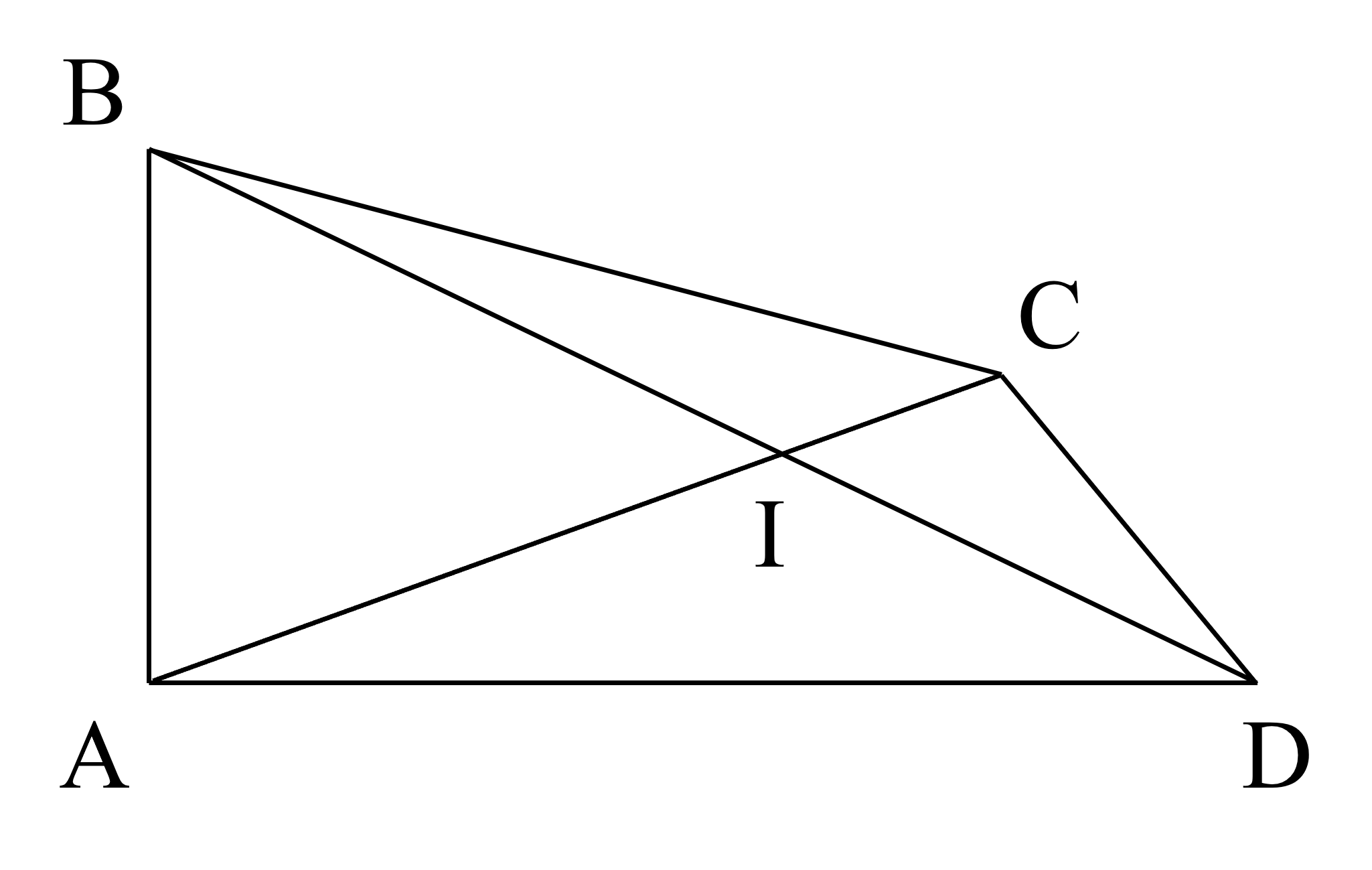
a) Điểm \(�\) và điểm \(�\) nằm trong góc \(� � �\).

b) (Học sinh nêu ra một góc bẹt sẽ đạt điểm tối đa phần này.)

Các góc bẹt trong hình là góc \(� � �\) và \(� � �\).

c) (Không trừ điểm học sinh khi đo góc có sai số từ \(1^{\circ}\) đến \(2^{\circ}\)).

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{� � �} = 18 0^{\circ}\)

\(\hat{� � �} = 7 0^{\circ}\)

\(\hat{� � �} = 13 5^{\circ}\)

\(\hat{� � �} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{� � �} ; \hat{� � �} ; \hat{� � �} ; \hat{� � �}\).

Số học sinh đạt loại Tốt là:

\(45. \frac{4}{15} = 12\) (học sinh)

Số học sinh đạt loại Khá là:

\(12. \frac{5}{3} = 20\) (học sinh)

Số học sinh được xếp loại Đạt là:

\(45 - 12 - 20 = 13\) (học sinh)

Đáp số: \(13\) học sinh

a) \(\frac{1}{2} - \frac{1}{2} : � = \frac{3}{4}\)

\(\frac{1}{2} : � = \frac{1}{2} - \frac{3}{4}\)

\(\frac{1}{2} : � = \frac{- 1}{4}\)

\(� = \frac{1}{2} : \&\text{nbsp}; \frac{- 1}{4}\)

\(� = - 2\)

b) \(\frac{� - 1}{15} = \frac{3}{5}\)

\(\frac{� - 1}{15} = \frac{9}{15}\)

\(� - 1 = 9\)

\(� = 10\)

c) \(� + 2 , 5 = 1 , 4\)

\(� = 1 , 4 - 2 , 5\)

\(� = - 1 , 1\)

a) \(� = 2 , 34 + 5 , 35 + 7 , 66 + 4 , 65\)

\(= \left(\right. 2 , 34 + 7 , 66 \left.\right) + \left(\right. 4 , 65 + 5 , 35 \left.\right)\)

\(= 10 + 10\)

\(= 20\)

b) \(� = 2 , 13.75 + 2 , 13.25\)

\(= 2 , 13. \left(\right. 75 + 25 \left.\right)\)

\(= 2 , 13.100\)

\(= 213\)

c) \(� = \frac{1}{3} - \frac{1}{3} : \frac{3}{4}\)

\(= \frac{1}{3} - \frac{1}{3} . \&\text{nbsp}; \frac{4}{3}\)

\(= \frac{1}{3} - \frac{4}{9}\)

\(= \frac{3}{9} - \frac{4}{9}\)

\(= \frac{- 1}{9}\)

B=1.44​+4.74​+7.104​+....+94.974​+97.1004​

\(� = 4 \left(\right. \frac{1}{1.4} + \frac{1}{4.7} + \frac{1}{7.10} + . . . . + \frac{1}{94.97} + \frac{1}{97.100} \left.\right)\)

\(� = \frac{4}{3} \left(\right. \frac{3}{1.4} + \frac{3}{4.7} + \frac{3}{7.10} + . . . . + \frac{3}{94.97} + \frac{3}{97.100} \left.\right)\)

\(� = \frac{4}{3} \left(\right. 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{10} + . . . . + \frac{1}{94} - \frac{1}{97} + \frac{1}{97} - \frac{1}{100} \left.\right)\)

\(� = \frac{4}{3} \left(\right. 1 - \frac{1}{100} \left.\right)\)

\(� = \frac{4}{3} . \frac{99}{100}\)

\(� = \frac{33}{25}\).

Vậy \(� = \frac{33}{25}\).

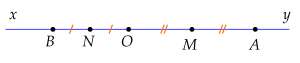
a) Ta có điểm \(�\) nằm giữa \(�\) và \(�\) \(\left(\right. �\) là trung điểm \(� � \left.\right)\) hay \(�\) và \(�\) cùng phía so với \(�\).

Mặt khác \(�\) thuộc tia \(� �\) nên \(�\) thuộc tia \(� �\).

Tương tự, điểm \(�\) nằm giữa \(�\) và \(�\) \(\left(\right. �\) là trung điểm \(� � \left.\right)\) hay \(�\) và \(�\) cùng phía so với \(�\).

Mặt khác \(�\) thuộc tia \(� �\) nên \(�\) thuộc tia \(� �\).

Mà \(� �\) và \(� �\) là hai tia đối nên \(�\) và \(�\) khác phía so với \(�\).

Vậy \(�\) nằm giữa \(�\) và \(�\).

b) Theo đề bài, ta có \(�\) là trung điểm của \(� �\) nên:

\(� � = � � = \frac{� �}{2} = 3\) cm.

Ta có \(�\) là trung điểm của \(� �\) nên:

\(� � = � � = \frac{� �}{2} = \frac{3}{2} = 1 , 5\) cm.

Vì \(�\) nằm giữa điểm \(�\) và \(�\) nên ta có:

\(� � + � � = � �\) hay \(� � = 3 + 1 , 5 = 4 , 5\) cm.

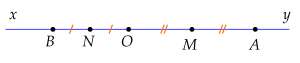
a) Ta có điểm \(�\) nằm giữa \(�\) và \(�\) \(\left(\right. �\) là trung điểm \(� � \left.\right)\) hay \(�\) và \(�\) cùng phía so với \(�\).

Mặt khác \(�\) thuộc tia \(� �\) nên \(�\) thuộc tia \(� �\).

Tương tự, điểm \(�\) nằm giữa \(�\) và \(�\) \(\left(\right. �\) là trung điểm \(� � \left.\right)\) hay \(�\) và \(�\) cùng phía so với \(�\).

Mặt khác \(�\) thuộc tia \(� �\) nên \(�\) thuộc tia \(� �\).

Mà \(� �\) và \(� �\) là hai tia đối nên \(�\) và \(�\) khác phía so với \(�\).

Vậy \(�\) nằm giữa \(�\) và \(�\).

b) Theo đề bài, ta có \(�\) là trung điểm của \(� �\) nên:

\(� � = � � = \frac{� �}{2} = 3\) cm.

Ta có \(�\) là trung điểm của \(� �\) nên:

\(� � = � � = \frac{� �}{2} = \frac{3}{2} = 1 , 5\) cm.

Vì \(�\) nằm giữa điểm \(�\) và \(�\) nên ta có:

\(� � + � � = � �\) hay \(� � = 3 + 1 , 5 = 4 , 5\) cm.

a)76.12+24.12-200=12.(76+24-200)=12.100=1200

b)3^4.36+4^3.81-100=81.36+64.81-100=81.(36+64-100)=81.0=0

a)VIII;XV;XXIV

b)0;3;6;9

a,5.4^x+4^2+x=336

5.4^x+4^2.4^x=336

5.4^x+4^2=336

5.4^x+16=336

4^x+(5.16)=336

4^x+80=336

4^x=336-80

4^x=256

x=256:4

x=64

vậy:x=64

b,x là bội của 11 và 10<x<40

vì x là B(11) nên B(11)={0;11;22;33;...} và 10<x<40

nên x={11;22;33}

vậy:x={11;22;33}