Diện tích khung ảnh là (17 + 2x)(25 + 2x).

Theo đề bài, diện tích khung ảnh lớn nhất là 513 cm²

Ta có phương trình:

(17 + 2x)(25 + 2x) = 513

⇔4x² + 84x + 425 = 513

⇔4x² + 84x - 88 = 0

⇔x² + 21x - 22 = 0

⇔(x + 22)(x - 1) = 0

⇔ x = -22(KTM) hoặc x = 1(TM)

Vậy độ rộng khung viền tối đa là là 1cm để diện tích của cả khung ảnh lớn nhất là 513(cm3)

​nΔ​​=(3;4);

nΔ1​​​=(5;−12).​

\(cos ⁡ \alpha = \mid cos ⁡ \left(\right. \overset{\rightarrow}{n_{\Delta}} ; \overset{\rightarrow}{n_{\Delta_{1}}} \left.\right) \mid = \frac{\mid 3.5 + 4. \left(\right. - 12 \left.\right) \mid}{5.13} = \frac{33}{65}\).

b) \(\left(\right. C \left.\right)\) có tâm \(I \left(\right. 3 ; - 2 \left.\right)\), bán kính \(R = 6\)

Đường thẳng \(d\) có dạng \(4 x - 3 y + m = 0\) (\(m\) khác \(7\))

\(d\) tiếp xúc \(\left(\right. C \left.\right)\) khi và chỉ khi \(d \left(\right. I , d \left.\right) = R \Leftrightarrow \frac{\mid 12 + 6 + m \mid}{5} = 6\).

Tìm được \(m = - 48\)(TM), \(m = 12\) (TM)

Vậy có hai đường thẳng \(d\) thỏa mãn là \(4 x - 3 y - 48 = 0\) và \(4 x - 3 y + 12 = 0\).

Ta có \(f \left(\right. x \left.\right) = x^{2} + 2 \left(\right. m - 1 \left.\right) x + m + 5\) 

 \(\Delta^{'} = \left(\right. m - 1 \left.\right)^{2} - \left(\right. m + 5 \left.\right) = m^{2} - 3 m - 4\)

Ta có:  \(a = 1 > 0\).

Để \(f \left(\right. x \left.\right)\) luôn dương (cùng dấu hệ số \(a\)) với mọi \(x \in \mathbb{R}\) thì \(\Delta^{'} < 0\) \(\Leftrightarrow m^{2} - 3 m - 4 < 0\).

Xét tam thức \(h \left(\right. m \left.\right) = m^{2} - 3 m - 4\) có \(\Delta_{m} = 9 - 4. \left(\right. - 4 \left.\right) = 25 > 0\) nên \(h \left(\right. m \left.\right)\) có hai nghiệm là \(m_{1} = - 1\) và \(m_{2} = 4\).

Ta có bảng xét dấu của \(h \left(\right. m \left.\right)\):

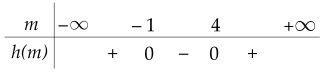
Do đó \(h \left(\right. m \left.\right) < 0\) với mọi \(x \in \left(\right. - 1 ; 4 \left.\right)\)

Hay \(\Delta^{'} < 0\) với mọi \(x \in \left(\right. - 1 ; 4 \left.\right)\)

Vậy \(x \in \left(\right. - 1 ; 4 \left.\right)\) thì tam thức bậc hai \(f \left(\right. x \left.\right) = x^{2} + \left(\right. m - 1 \left.\right) x + m + 5\) dương với mọi \(x \in \mathbb{R}\).

b) Bình phương hai vế ta được:

 \(2 x^{2} - 8 x + 4 = x^{2} - 4 x + 4\)

\(\Leftrightarrow x^{2} - 4 x = 0\)

Suy ra \(x=0\left(ktmdb\right)\) hoặc \(x=4\left(tmdb\right)\)

Vậy tập nghiệm \(S = 4\).