

Lê Song Phương
Giới thiệu về bản thân



































| a | b | c | d | e | |
| 5 | |||||
| 4 | |||||
| 3 | |||||
| 2 | |||||
| 1 |
Ta đánh dấu bảng 5x5 như trên và không mất tính tổng quát, giả sử quân mã ban đầu ở vị trí a1. Khi đó một đường đi của quân mã để đi hết tất cả các ô trên bàn cờ (với điều kiện mỗi ô chỉ được đi qua 1 lần) là:
a1-c2-e1-d3-e5-c4-a5-b3-c1-e2-d4-b5-a3-b1-d2-e4-c5-a4-b2-d1-e3-d5-b4-a2-c3.
Mình giải thích thêm trường hợp 1 nhé. Nếu như có 1 điểm \(A_m\) nằm ngoài 1 trong 2 đường tròn \(\left(A_i,1\right)\) và \(\left(A_j,1\right)\) thì 1 trong 2 đoạn \(A_mA_i\) và \(A_mA_j\) sẽ lớn hơn 1. Không mất tính tổng quát, giả sử đó là đoạn \(A_mA_i\). Khi đó \(A_mA_i>1\ge A_iA_j\), vô lí vì ta đã giả sử \(A_iA_j\) là đoạn có độ dài lớn nhất.
Gọi \(2n+1\) điểm đó là \(A_1,A_2,...,A_{2n+1}\). Do số điểm là hữu hạn nên tồn tại 1 đoạn thẳng \(A_iA_j\left(i\ne j\right)\) sao cho \(A_iA_j\) lớn nhất trong các \(A_kA_l\left(k\ne l;k,l=\overline{1,2n+1}\right)\).
TH1: Nếu \(A_iA_j\le1\), ta dựng 2 đường tròn \(\left(A_i,1cm\right)\) và \(\left(A_j,1cm\right)\). Dĩ nhiên nếu có bất kì điểm \(A_m\) nào nằm ngoài 2 đường tròn trên thì mâu thuẫn với giả thiết \(A_iA_j\) là đoạn thẳng có độ dài lớn nhất. Do đó, tất cả \(2n+1\) điểm sẽ nằm trong 2 đường tròn. Theo nguyên lí Dirichlet sẽ tồn tại 1 hình tròn chứa \(n+1\) điểm trong \(2n+1\) điểm đã cho. Đó là hình tròn cần tìm.
TH2: Nếu \(A_iA_j>1\), ta vẫn dựng 2 đường tròn \(\left(A_i,1cm\right)\) và \(\left(A_j,1cm\right)\). Khi đó nếu có bất kì điểm \(A_m\) nào nằm ở ngoài cả 2 hình tròn thì \(A_mA_i\) và \(A_mA_j\) đều lớn hơn 1. Khi đó bộ 3 điểm \(\left(A_i,A_j,A_m\right)\) mâu thuẫn với giả thiết trong 3 điểm bất kì luôn có 2 điểm có khoảng cách nhỏ hơn 1. Do vậy, tất cả các điểm đã cho đều nằm trong 2 đường tròn kể trên. Lại theo nguyên lí Dirichlet thì tồn tại \(n+1\) điểm thuộc cùng một hình tròn. Đấy chính là hình tròn cần tìm.
Vậy trong mọi trường hợp, ta đều tìm được 1 hình tròn bán kính 1cm chứa \(n+1\) điểm trong số \(2n+1\) điểm đã cho. Ta có đpcm.
Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)
ĐTXR \(\Leftrightarrow a=b=1\)
Vậy GTNN của P là 1 khi \(a=b=1\)
Ta có \(a+b^2\le\dfrac{a^2+1}{2}+b^2=\dfrac{a^2+2b^2+1}{2}\)
\(\Rightarrow\dfrac{2a^2}{a+b^2}\ge\dfrac{4a^2}{a^2+2b^2+1}=\dfrac{4a^4}{a^4+2b^2a^2+a^2}\). Lập 2 BĐT tương tự rồi áp dụng bất đẳng thức BCS, ta có:
\(\dfrac{2a^2}{a+b^2}+\dfrac{2b^2}{b+c^2}+\dfrac{2c^2}{c+a^2}\ge\dfrac{\left(2a^2+2b^2+2c^2\right)^2}{a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)+a^2+b^2+c^2}\) \(=\dfrac{4\left(a^2+b^2+c^2\right)^2}{\left(a^2+b^2+c^2\right)^2+3}\)\(=\dfrac{4.3^2}{3^2+3}=3\).
Mà \(a+b+c\le\sqrt{3\left(a^2+b^2+c^2\right)}=3\) nên ta có đpcm. ĐTXR \(\Leftrightarrow a=b=c=1\)
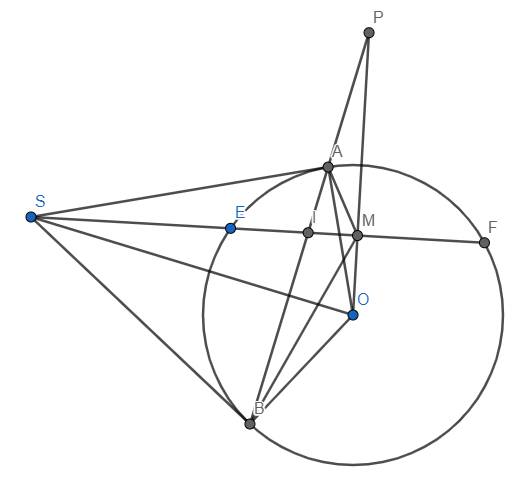
a) Do SA là tiếp tuyến tại A của (O) nên \(\widehat{OAS}=90^o\). Tương tự, ta có \(\widehat{OBS}=90^o\), suy ra \(\widehat{OAS}+\widehat{OBS}=180^o\). Do đó tứ giác SAOB nội tiếp. (đpcm)
Mặt khác, trong đường tròn (O) có M là trung điểm của dây EF nên \(OM\perp EF\) tại M hay \(\widehat{OMS}=90^o\). Từ đó suy ra \(\widehat{OMS}=\widehat{OAS}\),từ đó tứ giác OMAS nội tiếp. Vì vậy 5 điểm O, M, A, S, B cùng thuộc một đường tròn \(\Rightarrow\) Tứ giác SAMO nội tiếp (đpcm)
b) Ta thấy tứ giác OMAB nội tiếp nên \(\widehat{PMA}=\widehat{PBO}\). Từ đó dễ dàng suy ra \(\Delta PAM~\Delta POB\left(g.g\right)\Rightarrow\dfrac{PA}{PO}=\dfrac{PM}{PB}\) \(\Rightarrow PA.PB=PO.PM\) (đpcm)
c) Do tứ giác SAMB nội tiếp nên \(\widehat{SMB}=\widehat{SAB}\) và \(\widehat{SMA}=\widehat{SBA}\). Mặt khác, trong đường tròn (O), có 2 tiếp tuyến tại A và B cắt nhau tại S nên \(SA=SB\) hay \(\Delta SAB\) cân tại S \(\Rightarrow\widehat{SAB}=\widehat{SBA}\) \(\Rightarrow\widehat{SMB}=\widehat{SMA}\) hay MI là phân giác trong của \(\widehat{AMB}\) . Lại có \(MP\perp MI\) nên MP là phân giác ngoài của \(\widehat{AMB}\). Áp dụng tính chất đường phân giác, ta thu được \(\dfrac{IA}{IB}=\dfrac{MA}{MB}\) và \(\dfrac{PA}{PB}=\dfrac{MA}{MB}\). Từ đây suy ra \(\dfrac{IA}{IB}=\dfrac{PA}{PB}\) \(\Rightarrow PA.IB=PB.IA\) (đpcm)
\(a^3+b^3+c^3-3abc\) \(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2+2ab-ca-bc-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Vậy \(a^3+b^3+c^3=3abc\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a^2+b^2+c^2-ab-bc-ca=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a=b=c\end{matrix}\right.\)
Vậy để \(a^3+b^3+c^3=3abc\) thì \(a+b+c=0\) hoặc \(a=b=c\)
Đối với Python:
a) và b):
print("Nhập dãy số nguyên:")
ds=[int(i) for i in input().split()]
T=0
for i in range (0,len(ds)):
if ds[i]%2!=0:
T=T+1
print("Trong dăy có",T,"số lẻ.")
c)
print("Nhập dãy số nguyên:")
ds=[int(i) for i in input().split()]
S=0
P=1
for i in range (0,len(ds)):
if ds[i]%3==0:
S=S+ds[i]
print("Tổng các số chia hết cho 3 là",S)
for i in range (0,len(ds)):
if ds[i]%3==0:
P=P*ds[i]
print("Tích các số chia hết cho 3 là",P)
d)
print("Nhập dãy số nguyên:")
ds=[int(i) for i in input().split()]
ds.sort()
n=len(ds)
print(ds[n-1])
e)
print("Nhập dăy số nguyên:")
ds=[int(i) for i in input().split()]
for i in range (0,len(ds)):
if ds[i]%6==0:
print(ds[i])
Mình còn thiếu \(n\in\left\{39;40;41;42;43\right\}\)
Từ đề bài, ta thấy \(n\ge10\)
Với \(n=10\), xét khai triển \(R\left(n\right)=\left(3+x\right)^n\) \(\Rightarrow R\left(10\right)=\left(3+x\right)^{10}\) \(\sum\limits^{10}_{k=0}C^k_{10}3^{10-k}x^k\). Hệ số của số hạng chứa \(x^k\) là \(a_k=C^k_{10}.3^{10-k}\). Theo ycbt thì \(a_{10}\) là hệ số lớn nhất trong các \(a_i\left(i=\overline{0,10}\right)\) nên \(C^{10}_{10}.3^{10-10}=1\) là hệ số lớn nhất trong các hệ số. Nhưng \(a_5=C^5_{10}.3^5=61236>a_{10}\), mâu thuẫn.
Với \(n\ge11\), xét khai triển \(R\left(n\right)=\left(3+x\right)^n=\sum\limits^n_{k=0}C^k_n.3^{n-k}.x^k\). Hệ số của số hạng chứa \(x^k\) là \(a_k=C^k_n.3^{n-k}\). Do \(a_{10}\) là hệ số lớn nhất trong các số \(a_i\left(i=\overline{0,n}\right)\)nên \(\left\{{}\begin{matrix}a_{10}\ge a_9\\a_{10}\ge a_{11}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}C^{10}_n.3^{n-10}\ge C^9_n.3^{n-9}\\C^{10}_n.3^{n-10}\ge C^{11}_n.3^{n-11}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{n!}{10!\left(n-10\right)!}\ge\dfrac{n!}{9!\left(n-9\right)!}.3\\\dfrac{n!}{10!\left(n-10\right)!}.3\ge\dfrac{n!}{11!\left(n-11\right)!}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{10}\ge\dfrac{3}{n-9}\\\dfrac{3}{n-10}\ge\dfrac{1}{11}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}n\ge39\\n\le43\end{matrix}\right.\) \(\Leftrightarrow39\le n\le43\) (*)
(Ở đây mình chỉ so sánh hệ số \(a_{10}\) với \(a_9\) và \(a_{11}\) vì có xét với các \(a_i\) khác thì nó sẽ ra bất đẳng thức rộng hơn (*) nên mình quy về suy ra (*) luôn.)
Tổng các n là \(39+40+41+42+43=205\)