Ta có \(\sqrt{2022a+\dfrac{\left(b-c\right)^2}{2}}\) 

\(=\sqrt{2a\left(a+b+c\right)+\dfrac{b^2-2bc+c^2}{2}}\)

\(=\sqrt{\dfrac{4a^2+b^2+c^2+4ab+4ac-2bc}{2}}\)

\(=\sqrt{\dfrac{\left(2a+b+c\right)^2-4bc}{2}}\)

\(\le\sqrt{\dfrac{\left(2a+b+c\right)^2}{2}}\)

\(=\dfrac{2a+b+c}{\sqrt{2}}\).

Vậy \(\sqrt{2022a+\dfrac{\left(b-c\right)^2}{2}}\le\dfrac{2a+b+c}{\sqrt{2}}\). Lập 2 BĐT tương tự rồi cộng vế, ta được \(VT\le\dfrac{2a+b+c+2b+c+a+2c+a+b}{\sqrt{2}}\)

\(=\dfrac{4\left(a+b+c\right)}{\sqrt{2}}\) \(=\dfrac{4.1011}{\sqrt{2}}\) \(=2022\sqrt{2}\)

ĐTXR \(\Leftrightarrow\) \(\left\{{}\begin{matrix}ab=0\\bc=0\\ca=0\\a+b+c=1011\end{matrix}\right.\) \(\Leftrightarrow\left(a;b;c\right)=\left(1011;0;0\right)\) hoặc các hoán vị. Vậy ta có đpcm.

Ta thấy \(x>0\) nên ta có thể suy ra \(\sqrt{x}=\sqrt{4-2\sqrt{3}}\) \(=\sqrt{3-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}-1\right)^2}\) \(=\sqrt{3}-1\) (do \(\sqrt{3}-1>0\))

Từ đó \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) \(=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\) \(=\dfrac{\sqrt{3}}{\sqrt{3}-4}\) \(=\dfrac{\sqrt{3}\left(\sqrt{3}+4\right)}{\left(\sqrt{3}-4\right)\left(\sqrt{3}+4\right)}\) \(=\dfrac{3+4\sqrt{3}}{\left(\sqrt{3}\right)^2-4^2}\) \(=-\dfrac{3+4\sqrt{3}}{13}\)

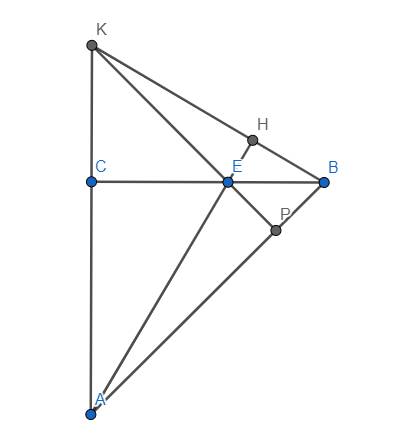
 Do \(CA=CB=a\) nên \(BE.BC+AC.AK=a\left(AK+BE\right)\) 

 Ta chứng minh \(AK+BE\) không đổi. Thật vậy, gọi P là giao điểm của KE và AB. Quan sát thấy E là trực tâm tam giác ABK \(\Rightarrow KP\perp AP\) tại P. Lại có \(\widehat{KAP}=45^o\) nên suy ra \(\widehat{AKP}=45^o\). Từ đó suy ta tam giác CEK cân tại C hay \(CE=CK\). 

 Từ đó \(AK+BE=AC+CK+BC-CE=2a\). Vậy \(BE.BC+AC.AK=2a^2\) không đổi (đpcm)

 Từ \(x^3+y^3+z^3=-3\) 

\(\Leftrightarrow2x^3+2y^3+2z^3=-6\) 

\(\Leftrightarrow2x^3+2y^3+2z^3=-3\left(x^2y+y^2z+z^2x\right)-3\left(xy^2+yz^2+zx^2\right)\)

\(\Leftrightarrow\left(x^3+3x^2y+3xy^2+y^3\right)+\left(y^3+3y^2z+3yz^2+z^3\right)+\left(z^3+3z^2x+3zx^2+x^3\right)=0\)

\(\Leftrightarrow\left(x+y\right)^3+\left(y+z\right)^3+\left(z+x\right)^3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+y+y+z+z+x=0\\x+y=y+z=z+x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+y+z=0\\x=y=z\end{matrix}\right.\)

 Xét TH \(x=y=z\), thay vào pt thứ 3 của hệ, ta có \(3x^3=-3\Leftrightarrow x=-1\) \(\Rightarrow\left(x;y;z\right)=\left(-1;-1;-1\right)\). Thử lại vào 2 pt đầu, ta thấy rõ ràng không thỏa mãn.

 Xét TH \(x+y+z=0\), ta sẽ có \(x^3+y^3+z^3=3xyz\) \(\Rightarrow xyz=-1\)

 Thay vào pt đầu tiên của hệ, thu được \(x^2y+y^2z+z^2x=-xyz\) \(\Leftrightarrow x^2y+y^2z+z^2x+xyz=0\). Tương tự, ta có \(xy^2+yz^2+zx^2+xyz=0\). Cộng theo vế 2 pt này, ta được \(\left(x+y\right)\left(y+z\right)\left(z+x\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\z+x=0\end{matrix}\right.\). Ta xét TH \(x+y=0\). Do \(x+y+z=0\) nên \(z=0\) và \(x=-y\), không thỏa mãn pt thứ 3. Tương tự với 2 trường hợp còn lại.

 Vậy hpt đã cho vô nghiệm.

 Nếu như thứ tự các câu hỏi trong đề là không quan trọng (ví dụ như đề gồm 3 câu được lấy từ câu 1,2,3 trong 9 câu cho trước giống với đề cũng gồm 3 câu đó nhưng thứ tự bị đảo lộn) thì ta làm như sau:

Câu hỏi đầu tiên sẽ có 9 cách chọn.

Câu hỏi thứ hai sẽ có 8 cách chọn.

Câu hỏi thứ ba sẽ có 7 cách chọn.

Vậy có thể soạn được nhiều nhất là \(9\times8\times7=504\) đề

 Nếu có phân biệt thứ tự các câu hỏi trong đề thì ta làm như sau:

 Ta cũng sẽ tính ra được có 504 đề khác nhau nhưng không kể thứ tự các câu trong đề. Do mỗi đề thi riêng biệt sẽ có tất cả là 6 "hoán vị" (nghĩa là 1 đề cũng gồm 3 câu đó nhưng khác thứ tự) nên ta lấy \(504\times6=3024\) đề. Vậy trong trường hợp mà có kể thứ tự các câu trong đề kiểm tra thì ta có thể lập được nhiều nhất 3024 đề.

Các điều kiện xác định hợp lại sẽ là \(\left\{{}\begin{matrix}2\le x\le4\\0\le y\le2\end{matrix}\right.\)

Ta có \(8\sqrt{xy-2y}-8y+4\) \(=8\sqrt{y\left(x-2\right)}-8y+4\) \(\le4\left(y+x-2\right)-8y+4\) (BĐT AM-GM) \(=4\left(x-y\right)-4\)

Do vậy, \(\left(x-y\right)^2=8\sqrt{xy-2y}-8y+4\le4\left(x-y\right)-4\) \(\Leftrightarrow\left(x-y\right)^2-4\left(x-y\right)+4\le0\) \(\Leftrightarrow\left(x-y-2\right)^2\le0\) \(\Leftrightarrow x-y-2=0\) \(\Leftrightarrow y=x-2\), điều này cũng thỏa mãn ĐTXR của BĐT \(8\sqrt{y\left(x-2\right)}=4\left(y+x-2\right)\). Do đó, pt đầu tiên của hệ \(\Leftrightarrow y=x-2\) hay \(x=y+2\)

Thay vào pt thứ 2 của hệ, ta có 

\(2\sqrt{2y-y^2}\left(\sqrt{4-2y}-2\sqrt{2y}+1\right)=4y+5\sqrt{2-y}-10\sqrt{y}\)

\(\Leftrightarrow\left(4-2y\right)\sqrt{2y}-4y\sqrt{4-2y}+2\sqrt{y\left(2-y\right)}=4y+5\sqrt{2-y}-10\sqrt{y}\)

 Mình mới làm được đến đây thôi. Mình phải đi ngủ rồi, thế nên mai mình suy nghĩ tiếp nhé.

 Gọi lượng kẹo mà Cassidy đã ăn trong ngày đầu tiên là \(x\), \(x\inℕ^∗\).   Khi đó lượng kẹo mà Kyle đã ăn trong ngày đầu tiên là \(\dfrac{4}{3}x\). Đến đây, ta thêm một điều kiện nữa là \(x⋮3\).

 Số kẹo còn lại là \(31-x-\dfrac{4}{3}x=31-\dfrac{7}{3}x\)

 Gọi số kẹo mà Cassidy đã ăn trong ngày thứ hai là \(y,y\inℕ^∗\). Khi đó số lượng kẹo mà Kyle đã ăn trong ngày thứ hai là \(\dfrac{3}{2}y\). Đến đây, ta thêm tiếp điều kiện \(y⋮2\). 

 Số kẹo còn lại là \(31-\dfrac{7}{3}x-y-\dfrac{3}{2}y=31-\dfrac{7}{3}x-\dfrac{5}{2}y\). 

 Sau ngày thứ hai, số kẹo đã hết nhẵn nên ta có pt \(31=\dfrac{7}{3}x+\dfrac{5}{2}y\) \(\Leftrightarrow14x+15y=186\) \(\Leftrightarrow y=\dfrac{186-14x}{15}\). Do \(x\inℕ^∗\) nên \(186-14x>0\Leftrightarrow x< \dfrac{186}{14}\Leftrightarrow x\le13\). 

 Do \(x⋮3\) nên \(x\in\left\{3;6;9;12\right\}\). Nếu \(x=3\Rightarrow y=\dfrac{48}{5}\left(loại\right)\)

Nếu \(x=6\Rightarrow y=\dfrac{34}{5}\left(loại\right)\)

Nếu \(x=9\Rightarrow y=4\left(nhận\right)\) 

Nếu \(x=12\Rightarrow y=\dfrac{6}{5}\left(loại\right)\)

Vậy \(x=9;y=4\), từ đây suy ra Cassidy đã ăn \(x+y=9+4=13\) miếng sô cô la.

Ta dùng công thức \(1+2+...+n=\dfrac{n\times\left(n+1\right)}{2}\). Khi đó

\(\dfrac{1}{1+2}=\dfrac{1}{\dfrac{2\times3}{2}}=\dfrac{2}{2\times3}\);

\(\dfrac{1}{1+2+3}=\dfrac{1}{\dfrac{3\times4}{2}}=\dfrac{2}{3\times4}\);

\(\dfrac{1}{1+2+3+4}=\dfrac{1}{\dfrac{4\times5}{2}}=\dfrac{2}{4\times5}\);

...;

\(\dfrac{1}{1+2+3+...+2020}=\dfrac{1}{\dfrac{2020\times2021}{2}}=\dfrac{2}{2020\times2021}\).

\(\Rightarrow\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+...+\dfrac{1}{1+2+3+...+2020}\)

\(=\dfrac{2}{2\times3}+\dfrac{2}{3\times4}+\dfrac{2}{4\times5}+...+\dfrac{2}{2020\times2021}\)

\(=2\left(\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+\dfrac{1}{4\times5}+...+\dfrac{1}{2020\times2021}\right)\)

\(=2\left(\dfrac{3-2}{2\times3}+\dfrac{4-3}{3\times4}+\dfrac{5-4}{4\times5}+...+\dfrac{2021-2020}{2020\times2021}\right)\)

\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\right)\)

\(=2\left(\dfrac{1}{2}-\dfrac{1}{2021}\right)\)

\(=\dfrac{2019}{2021}\)

 Trước hết, ta đi chứng minh một bổ đề sau: Nếu \(a+b+c=0\) thì \(a^3+b^3+c^3=3abc\). Thật vậy, ta phân tích 

 \(P=a^3+b^3+c^3-3abc\)

\(P=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)

\(P=\left(a+b+c\right)\left[\left(a+b\right)^2+\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)\)

\(P=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\).

Hiển nhiên nếu \(a+b+c=0\) thì \(P=0\) hay \(a^3+b^3+c^3=3abc\), bổ đề được chứng minh.

Do \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\) nên áp dụng bổ đề, ta được \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\).

Vì vậy \(\dfrac{yz}{x^2}+\dfrac{zx}{y^2}+\dfrac{xy}{z^2}=\dfrac{xyz}{x^3}+\dfrac{xyz}{y^3}+\dfrac{xyz}{z^3}\) \(=xyz\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)\) \(=xyz.\dfrac{3}{xyz}=3\). Ta có đpcm

 Vậy bạn ghi rõ ra là 2 ô có chung đỉnh cũng tính là kề nhau nhé. Thông thường khi nói đến 2 ô kề nhau mà không nói gì thêm thì người ta sẽ nghĩ là 2 ô có chung cạnh thôi.