

Bùi Khánh Hằng
Giới thiệu về bản thân



































a) Vẽ đồ thị (P)(P).
Bảng giá trị của yy tương ứng với giá trị của xx như sau:
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=2x2y=2x2 | 88 | 22 | 00 | 22 | 88 |
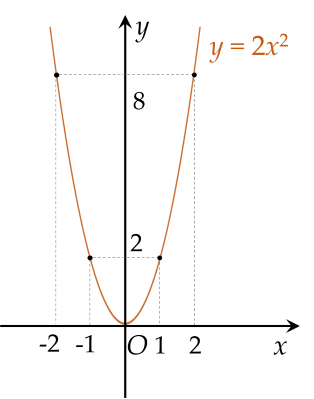
Vẽ các điểm A(−2;8 )A(−2;8 ), B(−1;2 )B(−1;2 ), O(0;0 )O(0;0 ), C(1;2 )C(1;2 ), D(2;8 )D(2;8 ) thuộc đồ thị hàm số y=2x2y=2x2 trong mặt phẳng OxyOxy.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số y=2x2y=2x2.
b) Phương trình hoành độ giao điểm của (P)(P) và (d)(d) là
2x2=2mx+12x2=2mx+1
2x2−2mx−1=02x2−2mx−1=0 (1)
Δ′=(−m)2−2.(−1)=m2+2>0Δ′=(−m)2−2.(−1)=m2+2>0 với mọi giá trị của mm
Nên phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của mm.
Suy ra (d)(d) luôn cắt (P)(P) tại hai điểm phân biệt với mọi giá trị của mm.
Theo định lí Viète ta có: {x1+x2=m(2)x1x2=−12(3)⎩⎨⎧x1+x2=m(2)x1x2=−21(3)
Ta có x1<x2x1<x2 mà x1x2=−12<0x1x2=2−1<0 suy ra x1<0<x2x1<0<x2.
Khi đó ∣x2∣−∣x1∣=2025∣x2∣−∣x1∣=2025
x2−(−x1)=2025x2−(−x1)=2025
x2+x1=2025x2+x1=2025
m=2025m=2025.
Vậy m=2025 thì thoản mãn đề bài
) Vẽ đồ thị (P)(P).
- Bảng giá trị của yy tương ứng với giá trị của xx như sau:
| xx | −4−4 | −2−2 | 00 | 22 | 44 |
| y=12x2y=21x2 | 88 | 22 | 00 | 22 | 88 |
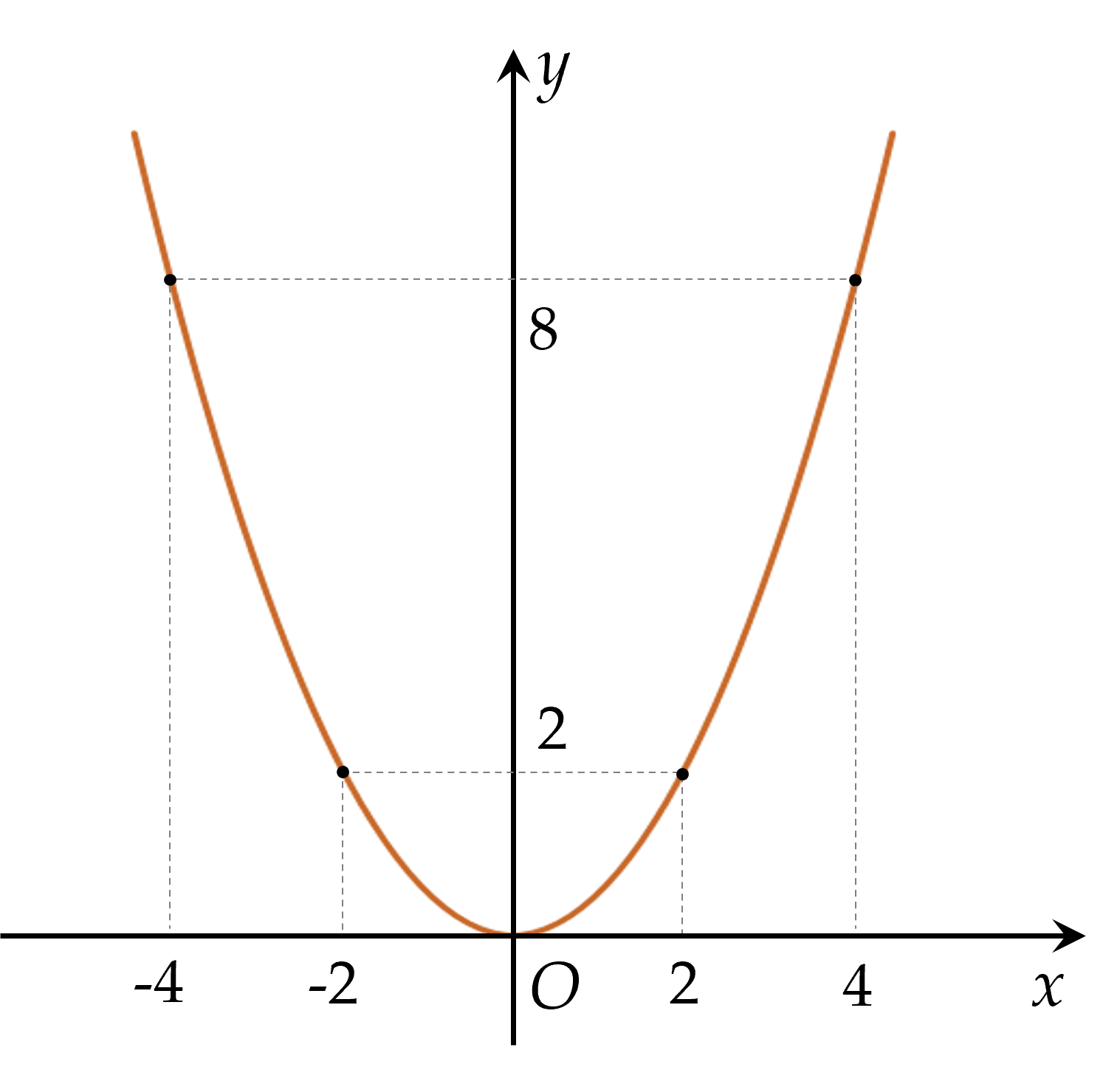
- Vẽ các điểm A(−4;8),B(−2;2),O(0;0),C(2;2),D(4;8)A(−4;8),B(−2;2),O(0;0),C(2;2),D(4;8) thuộc đồ thị hàm số y=12x2y=21x2 trong mặt phẳng OxyOxy.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số y=12x2y=21x2.
b) Phương trình hoành độ giao điểm: 12x2=x+12m2+m+121x2=x+21m2+m+1
x2−2x−m2−2m−2=0x2−2x−m2−2m−2=0 (*)
Để đường thẳng dd cắt (P)(P) tại hai điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt
Δ′>0Δ′>0
m2+2m+3>0m2+2m+3>0
(m+1)2+2>0(m+1)2+2>0
Do (m+1)2≥0(m+1)2≥0 với mọi mm nên (m+1)2+2>0(m+1)2+2>0 với mọi mm.
Do đó phương trình (*) luôn có hai nghiệm phân biệt với mọi mm
Suy ra đường thẳng dd luôn cắt (P)(P) tại hai điểm phân biệt có hoành độ x1;x2x1;x2.
Khi đó áp dụng định lí Viète ta có: x1+x2=2x1+x2=2; x1x2=−m2−2m−2x1x2=−m2−2m−2
Theo bài ra ta có: x13+x23=68x13+x23=68
(x1+x2)3−3x1x2(x1+x2)=68(x1+x2)3−3x1x2(x1+x2)=68
23−3(−m2−2m−2).2=6823−3(−m2−2m−2).2=68
6m2+12m−48=06m2+12m−48=0
m2+6m−8=0m2+6m−8=0 (**)
Vậy phương trình (**) có hai nghiệm phân biệt m1=2m1=2; m2=−4.m2=−4.
a) Vẽ đồ thị (P)(P)
- Bảng giá trị của yy tương ứng với giá trị của xx như sau:
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=x2y=x2 | 44 | 11 | 00 | 11 | 44 |
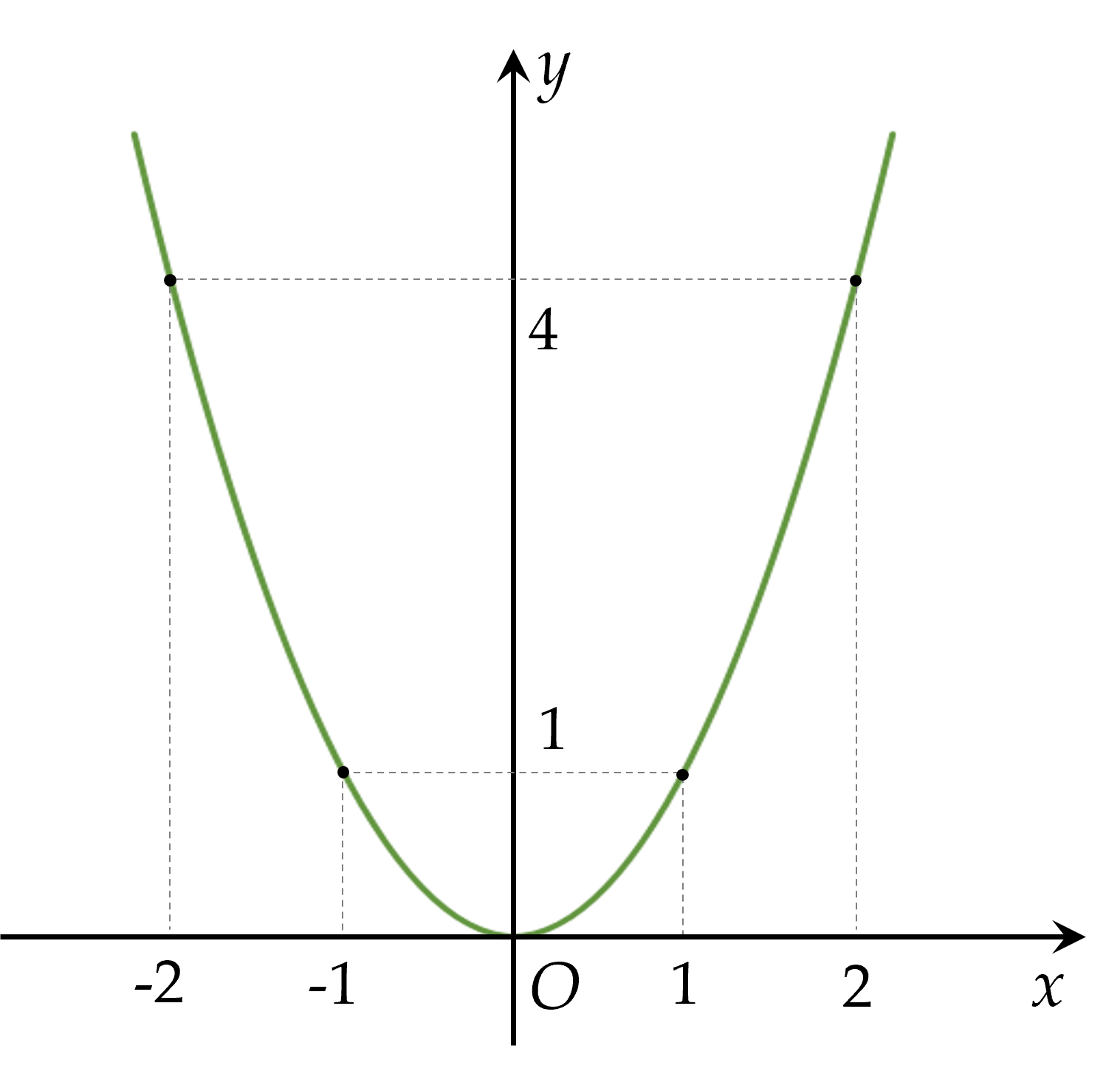
- Vẽ các điểm A(−2;4),B(−1;1),O(0;0),C(1;1),D(2;4)A(−2;4),B(−1;1),O(0;0),C(1;1),D(2;4) thuộc đồ thị hàm số y=x2y=x2 trong mặt phẳng OxyOxy.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số y=x2y=x2.
b) Xét phương trình hoành độ giao điểm:
x2=2x−3mx2=2x−3m
x2−2x+3m=0x2−2x+3m=0 (*)
Để đường thẳng (d)(d): y=2x−3my=2x−3m cắt đồ thị (P)(P) tại hai điểm phân biệt có hoành độ x1;x2x1;x2 thì phương trình (*) phải có hai nghiệm x1;x2x1;x2
Δ′=1−3m>0Δ′=1−3m>0
m<13m<31
Theo định lí Viète, ta có: {x1+x2=2x1x2=3m{x1+x2=2x1x2=3m
Vì x2x2 là nghiệm của phương trình (*) nên
x22−2x2+3m=0x22−2x2+3m=0
3m=2x2−x223m=2x2−x22
Suy ra x1x22−x2(2x2−x22+2x1)=12x1x22−x2(2x2−x22+2x1)=12
x1x22+x23−2x2(x1+x2)=12x1x22+x23−2x2(x1+x2)=12
x22(x1+x2)−2x2(x1+x2)=12x22(x1+x2)−2x2(x1+x2)=12
(x1+x2)(x22−2x2)=12(x1+x2)(x22−2x2)=12
2x22−4x2=122x22−4x2=12
x22−2x2=6x22−2x2=6
−3m−6=0−3m−6=0
m=−2m=−2 (tm)
Vậy m=−2m=−2 là giá trị cần tìm.
a) Vẽ parabol (P)(P) là đồ thị của hàm số y=x2y=x2
- Bảng giá trị của yy tương ứng với giá trị của xx như sau:
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=x2y=x2 | 44 | 11 | 00 | 11 | 44 |
- Vẽ các điểm A(−2;4),B(−1;1),O(0;0),C(1;1),D(2;4)A(−2;4),B(−1;1),O(0;0),C(1;1),D(2;4) thuộc đồ thị hàm số y=x2y=x2 trong mặt phẳng OxyOxy.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số y=x2y=x2.

b) Xét phương trình hoành độ giao điểm x2=−x−m+1x2=−x−m+1
x2+x+m−1=0x2+x+m−1=0 (1)
Để phương trình (1) có hai nghiệm phân biệt thì Δ>0Δ>0
12−4(m−1)>012−4(m−1)>0
m<54m<45
Khi đó áp dụng hệ thức Viète: x1+x2=−1; x1x2=m−1x1+x2=−1; x1x2=m−1.
Khi đó ta có: ∣x1−x2∣=2∣x1−x2∣=2
(x1−x2)2=4(x1−x2)2=4
(x1+x2)2−4x1x2=4(x1+x2)2−4x1x2=4
1−4(m−1)=41−4(m−1)=4
m=14m=41 (tm)
Vậy m=14m=41 là giá trị cần tìm.
Bảng giá trị của yy tương ứng với giá trị của xx như sau:
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=2x2y=2x2 | 88 | 22 | 00 | 22 | 88 |
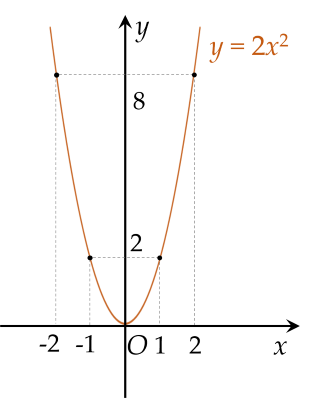
Vẽ các điểm A(−2;8 )A(−2;8 ), B(−1;2 )B(−1;2 ), O(0;0 )O(0;0 ), C(1;2 )C(1;2 ), D(2;8 )D(2;8 ) thuộc đồ thị hàm số y=2x2y=2x2 trong mặt phẳng OxyOxy.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số y=2x2y=2x2.
b) Phương trình hoành độ giao điểm của (d)(d) và (P)(P) là:
2x2=−2x+m2x2=−2x+m
2x2+2x−m=02x2+2x−m=0 (1)
Ta có Δ′=12−2(−m)=1+2mΔ′=12−2(−m)=1+2m.
Để (d)(d) cắt (P)(P) tại hai điểm phân biệt khi
Δ′>0Δ′>0
1+2m>01+2m>0
m>−12m>2−1
Với m>−12m>2−1 thì (d)(d) cắt (P)(P) tại hai điểm phân biệt có hoành độ x1;x2x1;x2.
Theo hệ thức Viète ta có: x1+x2=−1;x1x2=−m2x1+x2=−1;x1x2=2−m
Theo đề bài ta có: x1+x2−2x1x2=1x1+x2−2x1x2=1
−1−2−m2=1−1−22−m=1
−1+m=1−1+m=1
m=2m=2.
Vậy m=2m=2 thì (d)(d) cắt (P)(P) tại hai điểm phân biệt có hoành độ x1;x2x1;x2 thỏa mãn đề bài
a) Vẽ đồ thị hàm số y=x2y=x2 (P)(P)
- Bảng giá trị của yy tương ứng với giá trị của xx như sau:
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=x2y=x2 | 44 | 11 | 00 | 11 | 44 |
- Vẽ các điểm A(−2;4),B(−1;1),O(0;0),C(1;1),D(2;4)A(−2;4),B(−1;1),O(0;0),C(1;1),D(2;4) thuộc đồ thị hàm số y=x2y=x2 trong mặt phẳng OxyOxy.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số y=x2y=x2.

b) Khi m=2m=2 phương trình đường thẳng có dạng (d):y=2x+3(d):y=2x+3.
Hoành độ giao điểm của (P):y=x2(P):y=x2 và (d):y=2x+3(d):y=2x+3 là nghiệm của phương trình:
x2=2x+3x2=2x+3
x2−2x−3=0x2−2x−3=0
Vì a−b+c=1−(−2)+(−3)=0a−b+c=1−(−2)+(−3)=0 nên phương trình có hai nghiệm x1=−1x1=−1; x2=−ca=3x2=−ac=3.
Với x1=−1x1=−1 thì y1=(−1)2=1y1=(−1)2=1.
Với x2=3x2=3 thì y2=32=9y2=32=9.
Vậy ta có hai giao điểm của (P)(P) và (d)(d) là (−1;1)(−1;1) và (3;9)(3;9).
c) Xét phương trình hoành độ giao điểm của (P):y=x2(P):y=x2 và (d):y=mx+3(d):y=mx+3:
x2=mx+3x2=mx+3
x2−mx−3=0x2−mx−3=0 (1).
Để (d)(d) và (P)(P) luôn cắt nhau tại hai điểm phân biệt có hoành độ x1;x2x1;x2 thì phương trình (1) phải luôn có hai nghiệm phân biệt x1;x2x1;x2 thì Δ>0Δ>0
(−m)2−4.1.(−3)>0(−m)2−4.1.(−3)>0
m2+12>0m2+12>0 (luôn đúng với mọi mm)
Vậy với mọi mm thì phương trình (1) luôn có hai nghiệm phân biệt.
Theo hệ thức Viète, ta có: {x1+x2=mx1.x2=−3{x1+x2=mx1.x2=−3.
Thay x=0x=0 vào (1), ta có 02−m.0−3=−3≠002−m.0−3=−3=0 với mọi mm nên (1) luôn có hai nghiệm phân biệt khác 00 với mọi mm.
Theo bài ra ta có: 1x1+1x2=32x11+x21=23
2x2+2x1=3x1x22x2+2x1=3x1x2
2(x1+x2 )=3x1x22(x1+x2 )=3x1x2.
Thay hệ thức Viète, ta được: 2m=3.(−3)2m=3.(−3)
2m=−92m=−9
m=−92m=2−9.
Vậy m=−92m=−29 là giá trị cần tìm.
) Xét phương trình hoành độ giao điểm của (P)(P) và (d)(d) là :
x2=2x+m2x2=2x+m2
x2−2x−m2=0x2−2x−m2=0 (*)
Ta có Δ′=(−1)2−(−m)2=m2+1>0Δ′=(−1)2−(−m)2=m2+1>0 với mọi mm
Nên phương trình (*) luôn có hai nghiệm phân biệt, do đó (d)(d) luôn cắt (P)(P) tại hai điểm phân biệt.
b) Vì x1;x2x1;x2 là hoành độ giao điểm của (d)(d) và (P)(P) hay x1;x2x1;x2 là nghiệm của phương trình (*).
Theo hệ thức Viète ta có: x1+x2=2;x1x2=−m2x1+x2=2;x1x2=−m2.
Theo giả thiết: (x1+1)(x2+1)=−3(x1+1)(x2+1)=−3
x1x2+x1+x2+1+3=0x1x2+x1+x2+1+3=0
−m2+2+1+3=0 −m2+2+1+3=0
m2=6m2=6
m=±6m=±6.
Vậy m=±6m=±6 là các giá trị cần tìm.
a) Vì đường thẳng (d)(d) cắt trục tung tại điểm có tọa độ (0;−5)(0;−5) nên ta có:
2m+3=−52m+3=−5
2m=−82m=−8
m=−4m=−4.
Vậy với m=−4m=−4 thì đường thẳng (d)(d) cắt trục tung tại tọa độ (0;−5)(0;−5).
b) Phương trình hoành độ giao điểm của dd và (P)(P) là:
x2=2(m−1)x+2m+3x2=2(m−1)x+2m+3
x2−2(m−1)x−2m−3=0x2−2(m−1)x−2m−3=0 (*).
Ta có: Δ′=(m−1)2+2m+3=m2−2m+1+2m+3=m2+4Δ′=(m−1)2+2m+3=m2−2m+1+2m+3=m2+4.
Vì m2≥0m2≥0 với mọi mm nên Δ′=m2+4≥4>0Δ′=m2+4≥4>0 với mọi mm.
Vậy phương trình (*) có hai nghiệm phân biệt với mọi mm
Suy ra đường thẳng dd luôn cắt (P)(P) tại hai điểm phân biệt với mọi mm.
Theo định lí Viète ta có: {x1+x2=2(m−1)x1x2=−2m−3{x1+x2=2(m−1)x1x2=−2m−3
hay {xA+xB=2(m−1)xAxB=−2m−3{xA+xB=2(m−1)xAxB=−2m−3
Mà xA2+xB2=10xA2+xB2=10 nên
(xA+xB)2−2xAxB=10(xA+xB)2−2xAxB=10
4(m−1)2−2(−2m−3)=104(m−1)2−2(−2m−3)=10
4m2−8m+4+4m+6=104m2−8m+4+4m+6=10
4m2−4m=04m2−4m=0
4m(m−1)=04m(m−1)=0
m=0m=0; m=1m=1 (thỏa mãn điều kiện).
Vậy m∈{0;1}m∈{0;1}.
Ta có: 2x2+4x+m=02x2+4x+m=0 (*)
Δ′=22−2.m=4−2mΔ′=22−2.m=4−2m
Phương trình (*) có hai nghiệm x1;x2x1;x2 khi Δ′≥0Δ′≥0
4−2m≥04−2m≥0
m≤2m≤2
Với m≤2m≤2 thì phương trình (*) có hai nghiệm x1;x2x1;x2, theo hệ thức Viète:
x1+x2=−42=−2;x1+x2=2−4=−2; x1.x2=m2x1.x2=2m
Khi đó x12+x22=10x12+x22=10 trở thành
(x1+x2)2−2x1x2=10(x1+x2)2−2x1x2=10
(−2)2−2.m2=10(−2)2−2.2m=10
4−m=104−m=10
m=−6m=−6 (thỏa mãn).
Vậy m=-6 thì thoả mãn đề bài
Ta có: Δ′=22−(m−1)=5−mΔ′=22−(m−1)=5−m
Để phương trình có hai nghiệm x1;x2x
;x
thì Δ′≥0Δ
≥0 hay m≤5m≤5
Áp dụng định lí Viète ta có: x1+x2=4;x1x2=m−1x
+x
=4;x
x
=m−1
Theo bài ta ta có:
x12+x22=14x12+x22=14
(x1+x2)2−2x1x2=14(x
+x
)
−2x
x
=14
42−2(m−1)=1442−2(m−1)=14
m=2m=2 (thỏa mãn điều kiện
Vậy với m=2m=2 thì phương trình x2−4x+m−1=0x
−4x+m−1=0 có hai nghiệm x1;x2x
;x
thỏa mãn x12+x22=14x
+x
=14.