Gọi số hàng dọc chia được là \(x\) (hàng), \(x \in \mathbb{N}\) và \(x \geq 5\).

Theo bài ra ta có:48:x; \(18:x\)

Suy ra \(x \in\) ƯC\(\left(\right. 18 , 48 \left.\right)\).

Ta có: \(18 = 2. 3^{2}\); \(48 = 2^{4} . 3\)

Suy ra ƯCLN\(\left(\right. 18 , 48 \left.\right) = 2.3 = 6\)

Do đó,  \(x \in\) ƯC\(\left(\right. 18 , 48 \left.\right)\) = Ư(6)= {1;2;3;6}

Mà \(x \geq \&\text{nbsp}; 5\) nên \(x = 6\).

Vậy có thể xếp được thành \(6\) hàng dọc.

\(\left(\right. 454 - x \left.\right) + 4^{3} = 116\)

\(15\) chia hết cho \(1\); \(3\); \(5\) và \(15\).

Ta có bảng sau:

a) \(- 127 + 208 - 73 + 92\)

\(= \left(\right. - 127 - 73 \left.\right) + \left(\right. 208 + 92 \left.\right)\)

\(= - 200 + 300 = 100\).

b) \(2 353 - \left(\right. 473 + 2 153 \left.\right) + \left(\right. - 55 + 373 \left.\right)\)

\(= 2 353 - 473 - 2 153 - 55 + 373\)

\(= \left(\right. 2 353 - 2 153 \left.\right) + \left(\right. 373 - 473 \left.\right) - 55\)

\(= 200 - 100 - 55\)

\(= 45\).

Để chứng minh phân số tối giản, ta chứng minh ƯCLN của tử số và mẫu số là \(1\).

Goi ƯCLN \(\left(\right. n - 1 ; n - 2 \left.\right) = d \Rightarrow n - 1 : d\) và \(n - 2 : d\) 

\(\Rightarrow \left(\right. n - 1 \left.\right) - \left(\right. n - 2 \left.\right) : d \Rightarrow 1 : d\)

\(\Rightarrow d = 1\) với mọi \(n\).

Vậy với mọi \(n \in \mathbb{Z}\) thì \(M = \frac{n - 1}{n - 2}\) là phân số tối giản.

1. Trong hình vẽ có 4 bộ ba điểm thẳng là: 

+) \(A , C , D\)

+) \(A , B , E\)

+) \(C , E , F\)

+) \(D , E , B\)

2.

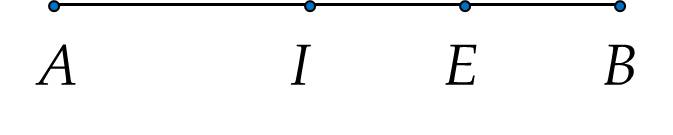
a) Theo hình vẽ, ta có: \(A I + I B = A B\)

Hay \(4 + I B = 9\)

\(I B = 9 - 4 = 5\) cm

b) Vì \(E\) là trung điểm của \(I B\) nên

\(E I = E B = \frac{I B}{2} = \frac{5}{2} = 2 , 5\) (cm)

Theo hình vẽ, ta có: \(A E = A I + I E = 4 + 2 , 5 = 6 , 5\) (cm)

1. Trong hình vẽ có 4 bộ ba điểm thẳng là: 

+) \(A , C , D\)

+) \(A , B , E\)

+) \(C , E , F\)

+) \(D , E , B\)

2.

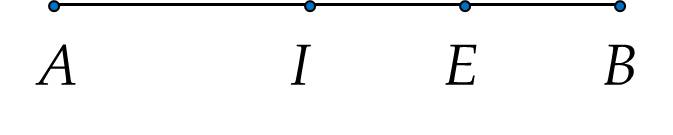
a) Theo hình vẽ, ta có: \(A I + I B = A B\)

Hay \(4 + I B = 9\)

\(I B = 9 - 4 = 5\) cm

b) Vì \(E\) là trung điểm của \(I B\) nên

\(E I = E B = \frac{I B}{2} = \frac{5}{2} = 2 , 5\) (cm)

Theo hình vẽ, ta có: \(A E = A I + I E = 4 + 2 , 5 = 6 , 5\) (cm)

Chiều dài đám đất là:

\(60. \frac{4}{3} = 80\) (m)

Diện tích đám đất là:

\(60.80 = 4 800\) (m\(^{2}\))

Diện tích trồng cây là:

\(4 800. \frac{7}{12} = 2 800\) (m\(^{2}\))

Diện tích còn lại là:

\(4 800 - 2 800 = 2 000\) (m\(^{2}\))

Diện tích ao cá:

\(2 000.30 \% = 600\) (m\(^{2}\))

a) \(\frac{- 5}{9} + \frac{8}{15} + \frac{- 2}{11} + \frac{4}{- 9} + \frac{7}{15} = \left(\right. \frac{- 5}{9} + \frac{- 4}{9} \left.\right) + \left(\right. \frac{8}{15} + \frac{7}{15} \left.\right) + \frac{- 2}{11}\)

\(= \frac{- 9}{9} + \frac{15}{15} + \frac{- 2}{11}\)

\(= - 1 + 1 + \frac{- 2}{11}\)

\(= 0 + \frac{- 2}{11} = \frac{- 2}{11}\).

b) \(\left(\right. \frac{7}{2} . \frac{5}{6} \left.\right) + \left(\right. \frac{7}{6} : \frac{2}{7} \left.\right)\)

\(= \left(\right. \frac{7}{2} . \frac{5}{6} \left.\right) + \left(\right. \frac{7}{6} . \frac{7}{2} \left.\right)\)

\(= \frac{7}{2} . \left(\right. \frac{5}{6} + \frac{7}{6} \left.\right)\)

\(= \frac{7}{2} . 2\)

\(= 7\)

a) Có \(\frac{- 3}{8} = \frac{- 9}{24} ; \frac{5}{- 12} = \frac{- 10}{12}\)

Vì \(\frac{- 9}{24} > \frac{- 10}{24}\) nên \(\frac{- 3}{8} > \frac{5}{- 12}\).

b) Có \(\frac{3131}{5252} = \frac{3131 : 101}{5252 : 101} = \frac{31}{52}\).

Vậy \(\frac{3131}{5252} = \frac{31}{52}\).

a) Diện tích mảnh vườn hình chữ nhật $ABCD$ là:

$35.20=700$ (m2
²)

b) Quãng đường ông Đức đi một vòng xung quanh vườn dài:

$(35+20).2=110$ (m)

c) Diện tích trồng hoa là: 700−35.20:2=350

$700-35.20:2=350$ (m²2
)

                                                          Đáp số: a) 700 m²

                                                                          b) 110 m

                                                                            c) 350 m²