

Nguyễn Bảo Phương Thảo
Giới thiệu về bản thân



































a: 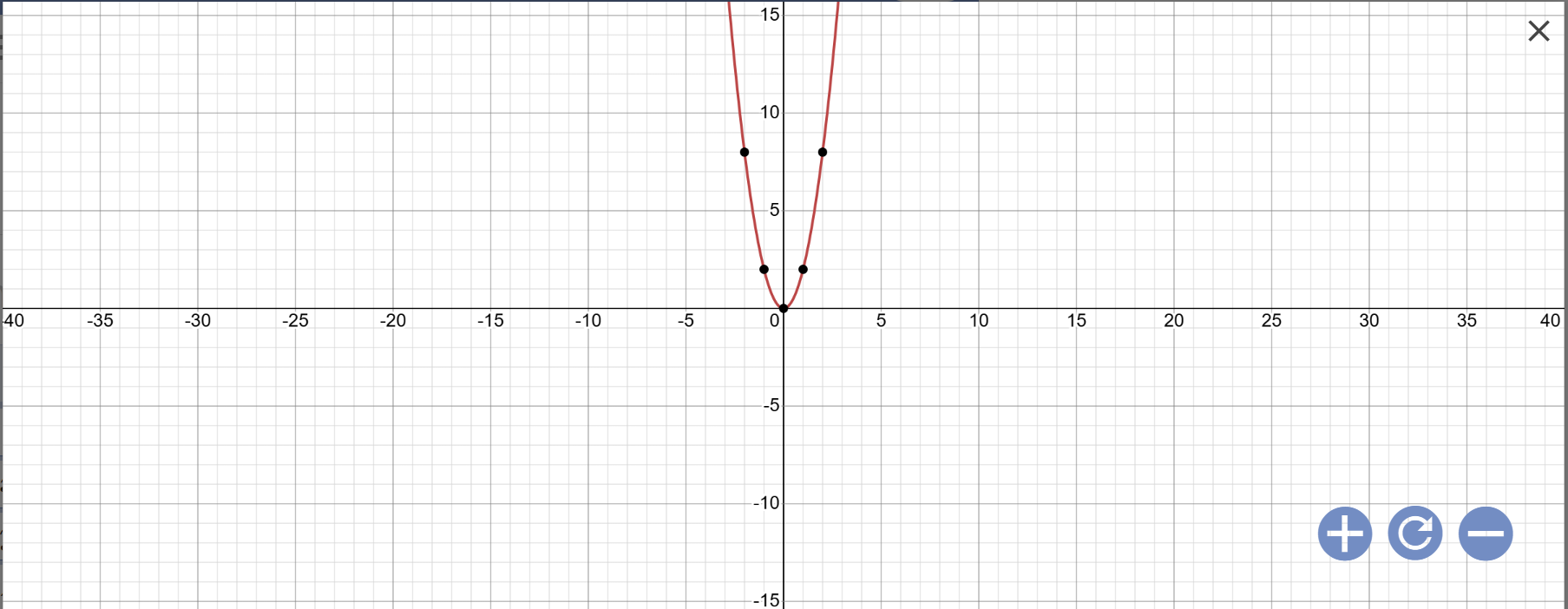
b: Phương trình hoành độ giao điểm là:
2x2=2mx+12x2=2mx+1
=>2x2−2mx−1=02x2−2mx−1=0
a=2; b=-2m; c=-1
Vì a⋅c=2⋅(−1)=−2<0a⋅c=2⋅(−1)=−2<0
nên (P) luôn cắt (d) tại hai điểm phân biệt
Theo vi-et, ta có:
{x1+x2=−ba=−(−2m)2=mx1x2=ca=−12⎩⎨⎧x1+x2=−ab=2−(−2m)=mx1x2=ac=−21
∣x2∣−∣x1∣=2025∣x2∣−∣x1∣=2025
=>(∣x2∣−∣x1∣)2=20252(∣x2∣−∣x1∣)2=20252
=>x22+x12−2∣x1x2∣=20252x22+x12−2∣x1x2∣=20252
=>(x1+x2)2−2x1x2−2∣x1x2∣=20252(x1+x2)2−2x1x2−2∣x1x2∣=20252
=>m2−2⋅−12−2⋅∣−12∣=20252m2−2⋅2−1−2⋅−21=20252
=>m2=20252m2=20252
=>[m=2025m=−2025[m=2025m=−2025
a: 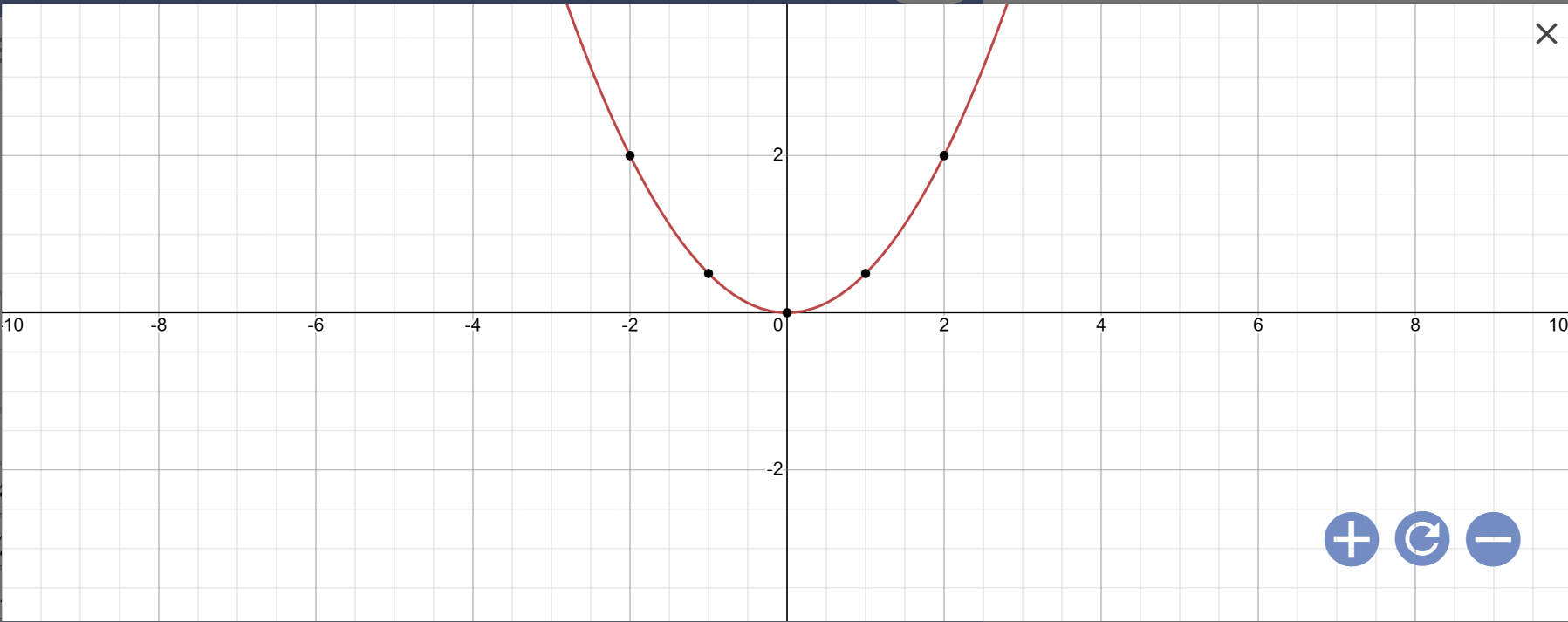
b: Phương trình hoành độ giao điểm là:
12x2=x+12m2+m+121x2=x+21m2+m+1
=>x2=2x+m2+2m+2x2=2x+m2+2m+2
=>x2−2x−(m2+2m+2)=0x2−2x−(m2+2m+2)=0
Δ=(−2)2−4⋅1⋅[−(m2+2m+2)]Δ=(−2)2−4⋅1⋅[−(m2+2m+2)]
=4+4(m2+2m+2)=4+4(m2+2m+2)
=4(m2+2m+3)=4(m2+2m+1+2)=4(m2+2m+3)=4(m2+2m+1+2)
=4(m+1)2+8>=8>0∀m=4(m+1)2+8>=8>0∀m
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
{x1+x2=−ba=2x1x2=ca=−(m2+2m+2)⎩⎨⎧x1+x2=−ab=2x1x2=ac=−(m2+2m+2)
x13+x23=68x13+x23=68
=>(x1+x2)3−3x1x2(x1+x2)=68(x1+x2)3−3x1x2(x1+x2)=68
=>23−3⋅2⋅[−(m2+2m+2)]=6823−3⋅2⋅[−(m2+2m+2)]=68
=>6(m2+2m+2)=606(m2+2m+2)=60
=>m2+2m+2=10m2+2m+2=10
=>m2+2m−8=0m2+2m−8=0
=>(m+4)(m-2)=0
=>[m=−4m=2[m=−4m=2
a: 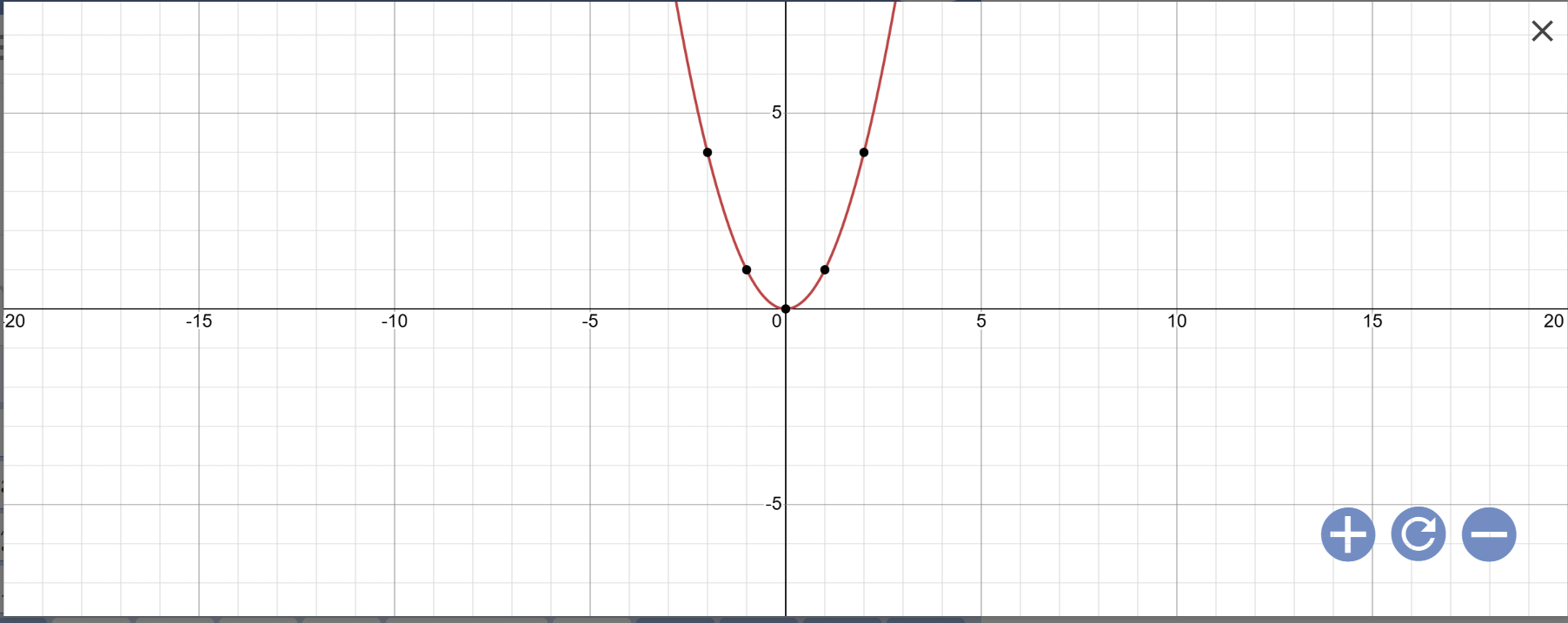
b: Phương trình hoành độ giao điểm là:
x2=2x−3mx2=2x−3m
=>x2−2x+3m=0x2−2x+3m=0
Δ=(−2)2−4⋅1⋅3m=−12m+4Δ=(−2)2−4⋅1⋅3m=−12m+4
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>-12m+4>0
=>-12m>-4
=>m<13m<31
Theo Vi-et, ta có:
{x1+x2=−ba=2x1x2=ca=3m⎩⎨⎧x1+x2=−ab=2x1x2=ac=3m
x1⋅x22−x2(3m+2x1)=12x1⋅x22−x2(3m+2x1)=12
=>x1⋅x22−x2(x1x2+2x1)=12x1⋅x22−x2(x1x2+2x1)=12
=>x1⋅x22−x1⋅x22−2x1x2=12x1⋅x22−x1⋅x22−2x1x2=12
=>-2*3m=12
=>-6m=12
=>m=-2(nhận)
a: 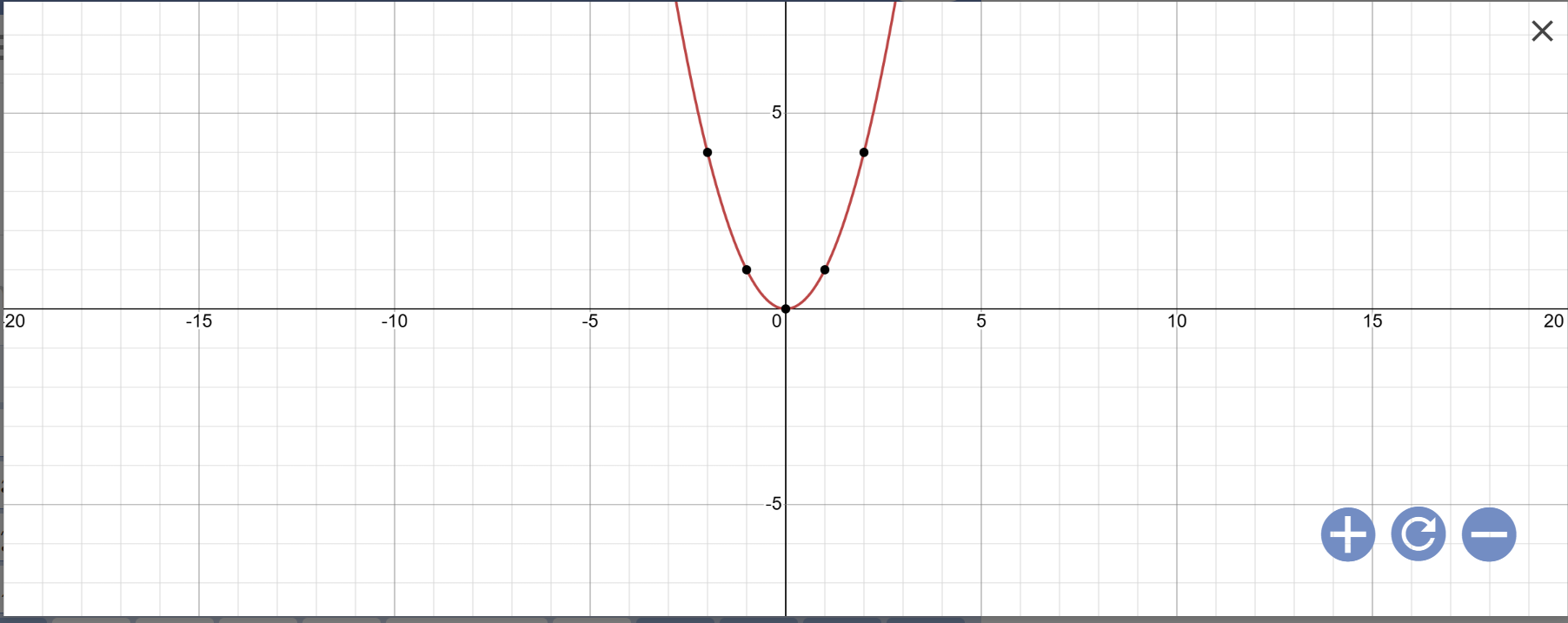
b: Khi m=2 thì (d): y=2x+3
Phương trình hoành độ giao điểm là;
x2=2x+3x2=2x+3
=>x2−2x−3=0x2−2x−3=0
=>(x-3)(x+1)=0
=>[x−3=0x+1=0⇔[x=3x=−1[x−3=0x+1=0⇔[x=3x=−1
Khi x=3 thì y=32=9y=32=9
Khi x=-1 thì y=(−1)2=1y=(−1)2=1
Vậy: (P) cắt (d) tại A(3;9); B(-1;1)
c: Phương trình hoành độ giao điểm là:
x2=mx+3x2=mx+3
=>x2−mx−3=0x2−mx−3=0
a=1; b=-m; c=-3
Vì a⋅c=1⋅(−3)=−3<0a⋅c=1⋅(−3)=−3<0
nên (P) luôn cắt (d) tại hai điểm phân biệt trái dấu
Theo Vi-et, ta có:
{x1+x2=−ba=mx1x2=ca=−3⎩⎨⎧x1+x2=−ab=mx1x2=ac=−3
1x1+1x2=32x11+x21=23
=>x1+x2x1x2=32x1x2x1+x2=23
=>m−3=32−3m=23
=>m=−92m=−29
a: 
b: Phương trình hoành độ giao điểm là:
2x2=−2x+m2x2=−2x+m
=>2x2+2x−m=02x2+2x−m=0
Δ =22−4⋅2⋅(−m)=8m+4Δ =22−4⋅2⋅(−m)=8m+4
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>8m+4>0
=>8m>-4
=>m>−12m>−21
Theo Vi-et, ta được:
{x1+x2=−ba=−22=−1x1x2=ca=−m2⎩⎨⎧x1+x2=−ab=−22=−1x1x2=ac=−2m
x1+x2−2x2x1=1x1+x2−2x2x1=1
=>−1−2⋅−m2=1−1−2⋅2−m=1
=>-1+m=1
=>m=2
a: 
b: Phương trình hoành độ giao điểm là:
x2=−x−m+1x2=−x−m+1
=>x2+x+m−1=0x2+x+m−1=0
Δ=12−4⋅1⋅(m−1)=1−4m+4=−4m+5Δ=12−4⋅1⋅(m−1)=1−4m+4=−4m+5
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>-4m+5>0
=>-4m>-5
=>m<54m<45
Theo Vi-et, ta có:
{x1+x2=−ba=−1x1x2=ca=m−1⎩⎨⎧x1+x2=−ab=−1x1x2=ac=m−1
∣x1−x2∣=2∣x1−x2∣=2
=>(x1−x2)2=2(x1−x2)2=2
=>(x1+x2)2−4x1x2=2(x1+x2)2−4x1x2=2
=>(−1)2−4(m−1)=2(−1)2−4(m−1)=2
=>1-4(m-1)=4
=>4(m-1)=-3
=>4m-4=-3
=>4m=1
=>m=14(nhận)m=41
a: Phương trình hoành độ giao điểm là:
x2=2x+m2x2=2x+m2
=>x2−2x−m2=0x2−2x−m2=0(1)
Δ=(−2)2−4⋅1⋅(−m2)=4m2+4>=4>0∀mΔ=(−2)2−4⋅1⋅(−m2)=4m2+4>=4>0∀m
=>Phương trình (1) luôn có hai nghiệm phân biệt
=>(P) luôn cắt (d) tại hai điểm phân biệt
b: Theo Vi-et, ta có:
{x1+x2=−ba=2x1x2=ca=−m2⎩⎨⎧x1+x2=−ab=2x1x2=ac=−m2
(x1+1)(x2+1)=−3(x1+1)(x2+1)=−3
=>x1x2+(x1+x2)+1=−3x1x2+(x1+x2)+1=−3
=>−m2+2+1=−3−m2+2+1=−3
=>−m2=−6−m2=−6
=>m2=6m2=6
=>[m=6m=−6[m=6m=−6
a: Thay x=0 và y=-5 vào (d), ta được:
2(m−1)⋅0+2m+3=−52(m−1)⋅0+2m+3=−5
=>2m+3=-5
=>2m=-8
=>m=-4
b: Phương trình hoành độ giao điểm là:
x2=2(m−1)x+2m+3x2=2(m−1)x+2m+3
=>x2−(2m−2)x−(2m+3)=0x2−(2m−2)x−(2m+3)=0
Δ=[−(2m−2)]2−4⋅1⋅[−(2m+3)]Δ=[−(2m−2)]2−4⋅1⋅[−(2m+3)]
=(2m−2)2+4(2m+3)=(2m−2)2+4(2m+3)
=4m2−8m+4+8m+12=4m2+16>=16>0∀m=4m2−8m+4+8m+12=4m2+16>=16>0∀m
=>Phương trình luôn có hai nghiệm phân biệt
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
{x1+x2=−ba=2m−2x1x2=ca=−(2m+3)⎩⎨⎧x1+x2=−ab=2m−2x1x2=ac=−(2m+3)
xA2+xB2=10xA2+xB2=10
=>(x1+x2)2−2x1x2=10(x1+x2)2−2x1x2=10
=>(2m−2)2−2⋅(−2m−3)=10(2m−2)2−2⋅(−2m−3)=10
=>4m2−8m+4+4m+6=104m2−8m+4+4m+6=10
=>4m2−4m=04m2−4m=0
=>4m(m-1)=0
=>m(m-1)=0
=>[m=0m−1=0⇔[m=0m=1[m=0m−1=0⇔[m=0m=1
Δ=(−m)2−4(m2−m−3)
=m2−4m2+4m+12=−3m2+4m+12=m2−4m2+4m+12=−3m2+4m+12
Để phương trình có hai nghiệm thì Δ>=0
=>−3m2+4m+12>=0−3m2+4m+12>=0
=>3m2−4m−12<=03m2−4m−12<=0
=>2−2103<=m<=2+210332−210<=m<=32+210
Theo Vi-et, ta có:
{x1+x2=−ba=mx1x2=ca=m2−m−3⎩⎨⎧x1+x2=−ab=mx1x2=ac=m2−m−3
x1;x2x1;x2 là độ dài các cạnh góc vuông của một tam giác vuông ABC có độ dài cạnh huyền là 2 nên ta có:
x12+x22=22x12+x22=22
=>(x1+x2)2−2x1x2=22(x1+x2)2−2x1x2=22
=>m2−2(m2−m−3)=4m2−2(m2−m−3)=4
=>m2−2m2+2m+6=4m2−2m2+2m+6=4
=>−m2+2m+2=0−m2+2m+2=0
=>m2−2m−2=0m2−2m−2=0
=>m2−2m+1−3=0m2−2m+1−3=0
=>(m−1)2−3=0(m−1)2−3=0
=>[m−1=3m−1=−3⇔[m=3+1(nhận)m=−3+1(nhận)[m−1=3m−1=−3⇔[m=3+1m=−3+1
Δ=(−2)2−4⋅1⋅(m−1)=4−4m+4=−4m+8
Để phương trình có hai nghiệm thì Δ>=0
=>−4m+8>=0−4m+8>=0
=>-4m>=-8
=>m<=2
Theo vi-et, ta có:
{x1+x2=−ba=2x1x2=ca=m−1⎩⎨⎧x1+x2=−ab=2x1x2=ac=m−1
x14−x13=x24−x23x14−x13=x24−x23
=>x14−x24=x13−x23x14−x24=x13−x23
=>(x1−x2)(x1+x2)(x12+x22)=(x1−x2)(x12+x22+x1x2)(x1−x2)(x1+x2)(x12+x22)=(x1−x2)(x12+x22+x1x2)
=>(x1−x2)⋅2⋅[(x1+x2)2−2x1x2]=(x1−x2)⋅[(x1+x2)2−x1x2](x1−x2)⋅2⋅[(x1+x2)2−2x1x2]=(x1−x2)⋅[(x1+x2)2−x1x2]
=>(x1−x2)2⋅[22−2(m−1)]=(x1−x2)(22−(m−1))(x1−x2)2⋅[22−2(m−1)]=(x1−x2)(22−(m−1))
=>(x1−x2)⋅2⋅(4−2m+2)=(x1−x2)⋅(4−m+1)(x1−x2)⋅2⋅(4−2m+2)=(x1−x2)⋅(4−m+1)
=>(x1−x2)(12−4m)−(x1−x2)(5−m)=0(x1−x2)(12−4m)−(x1−x2)(5−m)=0
=>(x1−x2)(12−4m−5+m)=0(x1−x2)(12−4m−5+m)=0
=>(x1−x2)(−3m+7)=0(x1−x2)(−3m+7)=0
=>[x1−x2=0−3m+7=0⇔[x1=x2m=73(loại)[x1−x2=0−3m+7=0⇔[x1=x2m=37(loại)
Nếu x1=x2x1=x2 thì x1=x2=x1+x22=22=1x1=x2=2x1+x2=22=1
x1x2=m−1x1x2=m−1
=>m-1=1
=>m=2