

Hưng
Giới thiệu về bản thân





































a. Vẽ đồ thị độ dịch chuyển – thời gian của Nam.
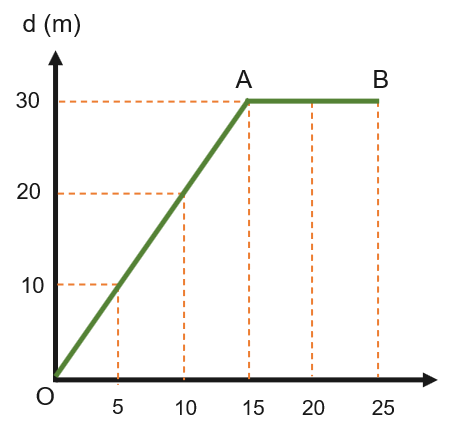
b. Mô tả chuyển động của Nam:
- Từ 0 – 15 giây: Nam chuyển động thẳng đều với vận tốc: v1=Δd1Δt1=3015=2v1=Δt1Δd1=1530=2 m/s
- Từ giây thứ 15 đến giây thứ 25: Nam đứng yên (dừng lại).
c. Vận tốc của Nam trong 15 s đầu là:
v1=Δd1Δt1=3015=2v1=Δt1Δd1=1530=2 m/s
Vận tốc của Nam trong suốt quá trình chuyển động:
v=ΔdΔt=3025=1,2v=ΔtΔd=2530=1,2 m/s
Đáp án:
a)
b)
c)
Giải thích các bước giải:
a)
b)
Theo ptpư:
c)
Theo ptpư:
Các khái niệm sự oxi hóa phản ứng hóa hợp, phản ứng phân hủy, sự cháy, sự oxi hóa chậm, phản ứng:
- Sự oxi hóa là sự tác dụng của oxi với một chất (chất đó có thể là đơn chất hoặc hợp chất).
- Phản ứng hóa hợp là phản ứng hóa học trong đó có một chất mới được tạo thành từ hai hay nhiều chất ban đầu.
- Phản ứng phân hủy là một phản ứng hóa học mà trong đó một chất tham gia có thể tạo thành hai hay nhiều chất mới.
- Sự cháy là phản ứng oxy hóa khử nhiệt độ cao giữa chất đốt và chất oxy hóa, có sinh ra ngọn lửa sáng
- Sự oxi hóa chậm là sự oxi hóa có tỏa nhiệt nhưng không phát sáng.
- Phản ứng thế là phản ứng hóa học, trong đó một nguyên tố có độ hoạt động hóa học mạnh sẽ thay thế cho nguyên tố có độ hoạt động hóa học yếu hơn trong hợp chất của nguyên tố này
PT:
Ta có:
a, Theo PT:
b, Theo PT:
c, PT:
Theo PT:
Mà: mCu (TT) = 2,88 (g)
PT:
Ta có:
a, Theo PT:
b, Theo PT:
c, PT:
Theo PT:
Mà: mCu (TT) = 2,88 (g)
a, Na2O + H2O → 2NaOH (Phản ứng hóa hợp)
b, 2H2 + O2 → 2H2O (Phản ứng hóa hợp)
c, 2KClO3 → 2KCl + 3O2 (Phản ứng phân hủy)
d, Mg + 2HCl → MgCl2 + H2 (Phản ứng thế)