Lê Ngọc Lam
Giới thiệu về bản thân




































a, Xét tam giác ABC có CD là phân giác góc ACB (GT)
\(\Rightarrow\dfrac{AC}{CB}=\dfrac{AD}{BD}\) (tính chất đường phân giác)
⇒ \(\dfrac{AC}{AD}=\dfrac{CB}{BD}=\dfrac{AC+CB}{AD+BD}=\dfrac{12+6}{12}=\dfrac{3}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{AC}{AD}=\dfrac{3}{2}\Rightarrow\dfrac{12}{AD}=\dfrac{3}{2}\Rightarrow AD=8cm\\\dfrac{CB}{BD}=\dfrac{3}{2}\Rightarrow\dfrac{6}{BD}=\dfrac{3}{2}\Rightarrow BD=4cm\end{matrix}\right.\)
Vậy a, AD=8cm; BD=4cm.
b,
Xét tam giác BAC có BN là đường phân giác của góc ABC(GT)
⇒ \(\dfrac{CN}{AN}=\dfrac{BC}{AB}=\dfrac{a}{b}\) (tính chất đường phân giác)
Xét tam giác CAB có CM là đường phân giác góc ACB (GT)
⇒ \(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\)( tính chất đường phân giác)
Xét tam giác ABC có
⇒\(\dfrac{BM}{AM}=\dfrac{CN}{AN}\left(CMT\right)\Rightarrow\dfrac{BM}{CN}=\dfrac{AM}{AN}\)
⇒ MN//BC(Thales đảo)
⇒ \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow\dfrac{AM}{b}=\dfrac{MN}{a}\)(1)
Có \(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\) (cmt)
⇒\(\dfrac{AM}{BM}=\dfrac{AC}{BC}=\dfrac{b}{a}\)
⇒ \(\dfrac{AM}{b}=\dfrac{BM}{a}=\dfrac{AM+BM}{a+b}=\dfrac{AB}{a+b}=\dfrac{b}{b+a}\)
⇒ \(AM=\dfrac{b^2}{a+b}\)
Thay vào (1) được
\(\dfrac{\dfrac{b^2}{a+b}}{b}=\dfrac{MN}{a}\Rightarrow\dfrac{b}{b+a}=\dfrac{MN}{a}\)
⇒ \(MN=\dfrac{b}{b+a}\times a=\dfrac{ab}{a+b}\)
Vậy \(MN=\dfrac{ab}{a+b}\).
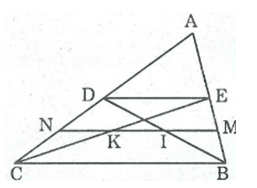
Vì CE,BD là trung tuyến ứng AB, AC trong tam giác ABC (GT)
⇒ AE = EB; AD = DC (TC)
Mà M, N lần lượt là trung điểm BE,DC(GT)
⇒ \(\dfrac{EM}{EB}=\dfrac{1}{2}\) và \(\dfrac{DN}{CD}=\dfrac{1}{2}\)
Hay \(\dfrac{EM}{AE}=\dfrac{1}{2}\) và \(\dfrac{DN}{AD}=\dfrac{1}{2}\)
⇒ \(\dfrac{EM}{AE}=\dfrac{DN}{AD}\)
Xét tam giác AMN có \(\dfrac{EM}{AE}=\dfrac{DN}{AD}\) (cmt)
⇒ ED//MN ( định lý Thales đảo)
Xét tam giác EBD có MI // ED ( I ϵ MN)
Mà M là trung điểm BE (GT)
⇒ I là trung điểm BD.
⇒ \(\dfrac{MI}{ED}=\dfrac{1}{2}\) (1)
Xét tam giác ECD có NK//ED (K ϵ MN)
Mà N là trung điểm CD (GT)
⇒ \(\dfrac{KN}{ED}=\dfrac{1}{2}\) (2)
Xét tam giác ABC có E, D lần lượt là trung điểm của AB, AC (GT)
⇒ ED là đường trung bình tam giác ABC (ĐN)
⇒\(\dfrac{ED}{BC}=\dfrac{1}{2}\) và ED//BC (TC) (3)
Từ (1), (2), (3) ⇒ \(\dfrac{MI}{BC}=\dfrac{KN}{BC}=\dfrac{1}{4}\) (4)
Xét tam giác EBC có KM // BC (//ED)
Mà M là trung điểm BE (GT)
⇒ K là trung điểm EC.
⇒ MK là đường trung bình tam giác EBC (ĐN)
⇒\(\dfrac{MK}{BC}=\dfrac{1}{2}\) hay \(\dfrac{MI+IK}{BC}=\dfrac{1}{2}\)
Mà \(\dfrac{MI}{BC}=\dfrac{1}{4}\) (CMT)
⇒ \(\dfrac{IK}{BC}=\dfrac{1}{4}\) (5)
Từ (4), (5) ⇒ MI = IK = KN
Vậy MI = IK = KN (ĐPCM)

Có BN và CM là đường trung tuyến ứng AC và AB (GT)
⇒ N và M lần lượt là trung điểm BN và CM (TC)
⇒ NA = NB và MA = MC.
Xét tam giác ABC có NA = NB(CMT) và MA = MC(CMT)
⇒ MN là đường trung bình tam giác ABC.
⇒ MN // BC và MN = \(\dfrac{1}{2}BC\) (TC) (1)
Xét tam giác GBC có DG = DB ( D là trung điểm BG) và EG = EC (E là trung điểm GC)
⇒ DE là đường trung bình tam giác BGC (ĐN)
⇒ DE // BC và DE = \(\dfrac{1}{2}BC\) (TC) (2)
Từ (1) và (2) ⇒ MN // DE và MN = ED
⇒ Từ giác NMED là hình bình hành (DHNB)
⇒ ME // ND (TC)
Vậy a, MN // DE (ĐPCM);
b, ND//ME (ĐPCM)
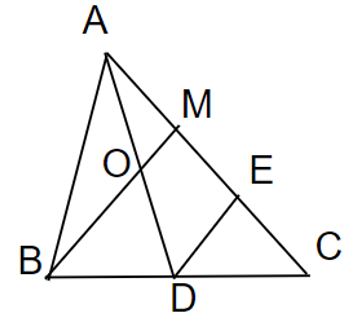
a, Gọi E là trung điểm MC.
Có AM = \(\dfrac{1}{2}MC\) (GT)
⇒ AM = ME= EC
Có AD là đường trung tuyến của tam giác ABC (GT)
⇒ D là trung điểm BC (TC)
⇒ BD = CD
Xét tam giác BCM có ME = EC (CMT) và DB = DC (CMT)
⇒ DE là đường trung bình của tam giác BCM (ĐN)
⇒ DE // BM (TC)
Xét tam giác ADE có AM = ME (CMT) VÀ BM // DE (CMT) hay OM // DE (O ϵ BM)
⇒ OA = OD
Hay O là trung điểm của AD
Vậy O là trung điểm của AD (ĐPCM)
b, Có DE là đường trung bình tam giác BCM (CMT)
⇒ DE = \(\dfrac{1}{2}BM\) (TC)
Xét tam giác ADE có OA = OD (CMT) và AM = ME (CMT)
⇒ OM là đường trung bình tam giác ADE (ĐN)
⇒ OM =\(\dfrac{1}{2}DE=\dfrac{1}{2}\times\dfrac{1}{2}BM=\dfrac{1}{4}BM\)
⇒ OM = \(\dfrac{1}{4}MB\)
Vậy OM = \(\dfrac{1}{4}MB\) (đpcm)
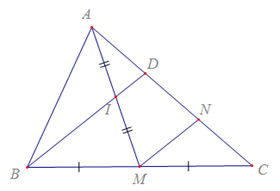
a, Qua M kẻ MN // BD (N ϵ AC)
Xét tam giác AMN có I là trung điểm AM (GT)
Mà ID // MN (BD // MN)
⇒ D là trung điểm của AN
⇒ AD=DN (TC) (1)
⇒ ID là đường trung bình của tam giác AMN
Có AM là trung tuyến của BC (GT)
⇒ M là trung điểm BC (GT)
Xét tam giác BCD có M là trung điểm BC (CMT)
Mà MN // BD (GT)
⇒ MN là đường trung bình tam giác BCD
⇒ ND = NC (TC) (2)
Từ (1), (2) ⇒ AD=DN=NC
⇒ AD = \(\dfrac{1}{2}DC\)
Vậy ⇒ AD = \(\dfrac{1}{2}DC\) (đpcm)
b, Từ câu a có ID là đường trung bình tam giác AMN (CMT)
⇒ 2 ID = MN (TC) (3)
Có MN là đường trung bình tma giác BCD (CMT)
⇒ 2 MN = BD (TC) (4)
Từ (3) và (4) ⇒ 4 ID = BD
Vậy BD dài gấp 4 lần ID.
Xét tam giác ABC có: \(BC\perp AB'\) ( từ hình vẽ) và \(B'C'\perp AB'\) (từ hình vẽ)
⇒ BC//B'C'
Xét tam giác AB'C' có: BC//B'C' (cmt)
⇒ \(\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\) (Hệ quả định lí Thales)
hay \(\dfrac{x}{x+h}=\dfrac{a}{a'}\)
⇒ ax' = a (x+h) = ax+ah
⇒ ah = x (a'-a)
⇒ \(x=\dfrac{ah}{a'-a}\)
Vậy \(x=\dfrac{ah}{a'-a}\) (đpcm).
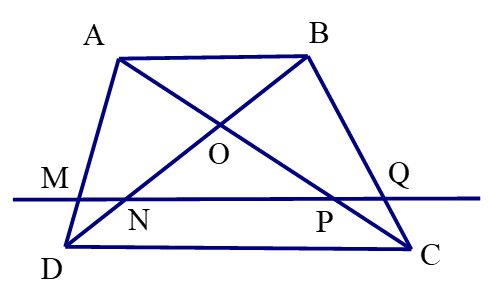
Xét tam giác ABD có: MN//AB (GT)
⇒ \(\dfrac{DN}{BD}=\dfrac{MN}{AB}\) (Hệ quả định lí Thales) (1)
Xét tam giác ACB có: PQ//AB (GT)
⇒ \(\dfrac{CQ}{CB}=\dfrac{PQ}{AB}\) (Hệ quả định lí Thales) (2)
Có: AB//CD (GT)
Mà NQ//AB (GT)
⇒ NQ//CD.
Xét tam giác BDC có: QN//CD (cmt)
⇒ \(\dfrac{DN}{DB}=\dfrac{CQ}{CB}\) (Định lí Thales) (3)
Từ (1), (2), (3) ⇒ \(\dfrac{MN}{AB}=\dfrac{PQ}{AB}\left(=\dfrac{DN}{DB}=\dfrac{CQ}{CB}\right)\)
⇒ MN = PQ
Vậy MN = PQ (đpcm).

Gọi CE là đường trung tuyến của AB trong tam giác ABC.
Xét tam giác ABC có:
G là trọng tâm (GT) và CE là đường trung tuyến ứng AB (cmt)
⇒ \(GE=\dfrac{1}{3}CE\) (tc) ⇒ \(\dfrac{CE}{GE}=\dfrac{1}{3}\)
Xét tam giác CEB có: d//AB hay BE//GM (G,M ϵ d; E ϵ AB)
⇒ \(\dfrac{BM}{BC}=\dfrac{GE}{CE}=\dfrac{1}{3}\) (Định lí Thales)
⇒ \(BM=\dfrac{1}{3}BC\)
Vậy \(BM=\dfrac{1}{3}BC\) (đpcm).
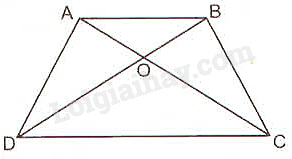
Xét tam giác ABO có: AB//CD (GT)
⇒ \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\) (Định lí Thales)
⇒ \(OA\times OD=OB\times OC\)
Vậy \(OA\times OD=OB\times OC\) (đpcm).