

Nguyễn Ngọc Anh Minh
Giới thiệu về bản thân



































6C=1.3.6+3.5.6+5.7.6+...+99.101.6=
=1.3.(5+1)+3.5.(7-1)+5.7.(9-3)+...+99.101.(103-97)=
=1.3+1.3.5-1.3.5+3.5.7-3.5.7+5.7.9-...-97.99.101+99.101.103=
=1.3+99.101.103
C=(1.3+99.101.103):6
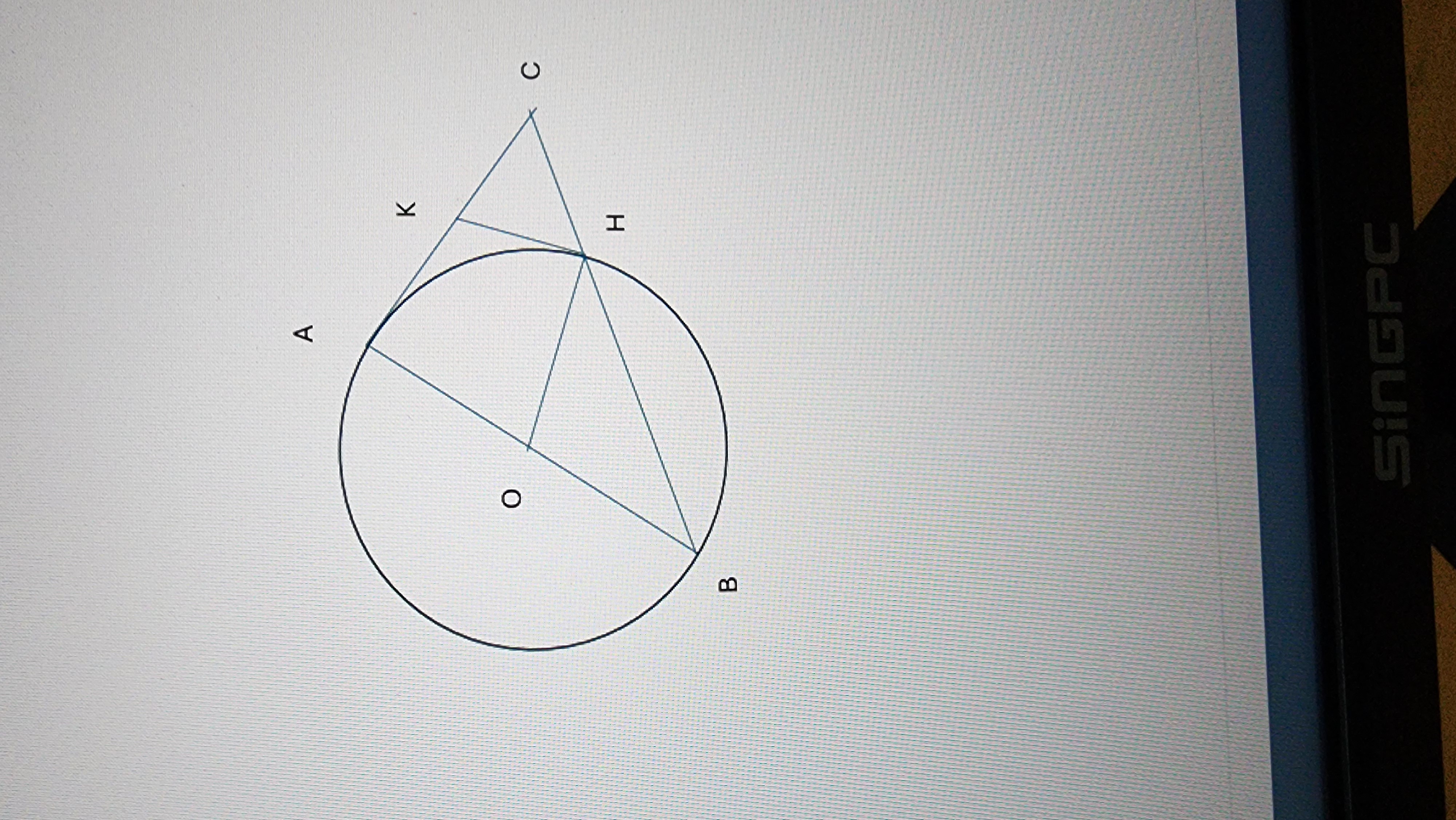
a/
Xét (O) có
\(\hat{AHB}=90^{o}\) (Góc nt chắn nửa đường tròn)
=> △AHB vuông
b/
\(OA=OH=R\rArr\Delta OAH\) cân tại H
\(\rArr\hat{OAH}=\hat{OHA}\)
Xét tg vuông AHC có
\(AK=CK\rArr KH=AK=CK=\frac{AC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\rArr\Delta KHA\) cân tại K
\(\rArr\hat{KAH}=\hat{KHA}\)
\(\rArr\hat{OAH}+\hat{KAH}=\hat{OHA}+\hat{KHA}\rArr\hat{OAK}=\hat{OHK}\)
Mà \(\hat{OAK}=90^{o}\rArr\hat{OHK}=90^{o}\)
=> KH là tiếp tuyến của (O)
c/
Ta có A và H cùng nhìn OK dưới 2 góc bằng nhau và \(=90^{o}\)
=> A và H cùng thuộc đường tròn đường kính OK => A;K;H;O cùng nằm trên 1 đường tròn
a/ Khi \(m=-2\)
\(\left(1\right)\lrArr x^2-3x+2=0\)
PT có dạng \(a+b+c=0\)
\(x1=1;x2=\frac{c}{a}=2\)
b/
Để (1) có 2 nghiệm phân biệt
\(\Delta=9-4\left(m+4\right)=-4m+5>0\)
\(\lrArr4m-5<0\lrArr m<\frac54\)
Ta có
\(x2\left(x2-1\right)+x1\left(x1-1\right)=2\)
\(\lrArr x2^2-x2+x1^2-x1-2=0\)
\(\lrArr\left(x1+x2\right)^2-2.x1.x2-\left(x1+x2\right)-2=0\) (2)
Áp dụng định lý Viet
\(x1+x2=-\frac{b}{a}=3\)
\(x1.x2=\frac{c}{a}=m+4\)
Thay vào (2) rồi giải PT ẩn m đối chiếu với ĐK \(m<\frac54\)
Bạn tự làm nốt nhé
\(C=\frac{2\left(x^2+2x+4\right)}{\left(x-1\right)\left(x+1\right)\left(x-3\right)}.\frac{\left(x+1\right)\left(x-3\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\)
\(=\frac{2}{\left(x-1\right)\left(x-2\right)}\)
=-46.54-2.46+46.54-2.54=
=-2(46+54)=-2.100=-200
\(\frac{2n}{n-2}=\frac{2\left(n-2\right)+4}{n-2}=2+\frac{4}{n-2}\)
2n⋮n-2 khi 4⋮n-2
\(\rArr\left(n-2\right)=\left\lbrace-4;-2-1;1;2;4\right\rbrace\)
\(\rArr n=\left\lbrace-2;0;1;3;4;6\right\rbrace\)
\(M<\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\cdots+\frac{1}{2020.2021}=\)
\(=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+\cdots+\frac{2021-2020}{2020.2021}=\)
\(1-\frac12+\frac12-\frac13+\frac13-\frac14+\cdots+\frac{1}{2020}-\frac{1}{2021}=\)
\(1-\frac{1}{2021}=\frac{2020}{2021}=N\)
\(\frac{a}{b}-\frac{a+m}{b+m}=a\left(b+m\right)-b\left(a+m\right)=\)
\(ab+am-ab-bm=m\left(a-b\right)\)
+ Nếu \(a>b\rArr m\left(a-b\right)>0\rArr\frac{a}{b}>\frac{a+m}{b+m}\)
+ Nếu \(a

Gọi G là giao của AC với DM
Xét △BCD có
MB=MC (gt); OB=OD (trong hbh 2 đường chéo cắt nhau tại trung điểm mối đường)
=> G là trọng tâm của △BCD
\(\rArr\frac{CG}{OC}=\frac23\) Mà \(OC=\frac{AC}{2}\rArr\frac{CG}{OC}=\frac{CG}{\frac{AC}{2}}=\frac{2CG}{AC}=\frac23\rArr\frac{CG}{AC}=\frac13\rArr\frac{CG}{GA}=\frac12\)
Xét △SAC có
\(\frac{CG}{GA}=\frac12\left(\operatorname{cm}t\right)\)
\(NS=2NC\rArr\frac{NC}{NS}=\frac12\)
\(\rArr\frac{CG}{GA}=\frac{NC}{NS}\) => SA//NG (Talet đảo)
Mà NG∈(DMN) => SA//(DMN)
a2024b chia hết cho 45
=> a2024b đồng thời chia hết cho 5 và 9
a2024b chia hết cho 5 => b=0 hoặc b=5
+ Với b=0
=> a2024b=a20240 chia hết cho 9 => a=1
ta có số 120240 thỏa mãn đề bài
+ Với b=5
=> a2024b=a20245 chia hết cho 9 => a=5
ta có số 520245 thỏa mãn đề bài