def should_swap(a, b):

if a % 2 != 0 and b % 2 == 0:

return True

elif a % 2 == b % 2 and a > b:

return True

else:

return False

def bubble_sort_chan_le(arr):

n = len(arr)

for i in range(n - 1):

for j in range(0, n - i - 1):

if should_swap(arr[j], arr[j + 1]):

arr[j], arr[j + 1] = arr[j + 1], arr[j]

my_list = [64, 34, 25, 12, 22, 11, 90]

bubble_sort_chan_le(my_list)

print("Mảng đã sắp xếp:", my_list)

def should_swap(a, b):

if a % 2 != 0 and b % 2 == 0:

return True

elif a % 2 == b % 2 and a > b:

return True

else:

return False

def bubble_sort_chan_le(arr):

n = len(arr)

for i in range(n - 1):

for j in range(0, n - i - 1):

if should_swap(arr[j], arr[j + 1]):

arr[j], arr[j + 1] = arr[j + 1], arr[j]

my_list = [64, 34, 25, 12, 22, 11, 90]

bubble_sort_chan_le(my_list)

print("Mảng đã sắp xếp:", my_list)

kiếm thử phần mềm giúp đảm bảo chất lượng và độ tin cậy cảu phần mềm

Ta có \(4^{x} - 3. 2^{x + 2} + m = 0 \Leftrightarrow 4^{x} - 12. 2^{x} + m = 0\) (1)

Đặt \(t = 2^{x} , \left(\right. t > 0 \left.\right)\) phương trình (1) trở thành \(t^{2} - 12 t + m = 0\) \(\left(\right. 2 \left.\right)\).

YCBT \(\Leftrightarrow \left(\right. 2 \left.\right)\) có hai nghiệm dương phân biệt \(t = t_{1} ; t = t_{2}\) và log⁡2t1+log⁡2t2=5log2​t1​+log2​t2​=5

\(\Leftrightarrow \left{\right. & \Delta^{'} > 0 \\ & S > 0 \\ & P > 0 \\ & t_{1} . t_{2} = 32\)

\(\Leftrightarrow \left{\right. & 36 - m > 0 \\ & m > 0 \\ & m = 32\)

\(\Leftrightarrow m = 32\)

\(\Delta S A B\) vuông tại \(A \Rightarrow S A ⊥ A B\).

\(\Delta S A D\) vuông tại \(A \Rightarrow S A ⊥ A D\).

Suy ra \(S A ⊥ \left(\right. A B C D \left.\right)\).

Gọi \(I\) là giao điểm của \(B M\) và \(A D\).

Dựng \(A H\) vuông góc với \(B M\) tại \(H\).

Dựng \(A K\) vuông góc với \(S H\) tại \(K\).

\(& S A ⊥ \left(\right. A B C D \left.\right) \\ & B M \subset \left(\right. A B C D \left.\right) \left.\right} \Rightarrow S A ⊥ B M\) mà \(B M ⊥ A H\)

\(\Rightarrow B M ⊥ \left(\right. S A H \left.\right)\).

Ta có \(& B M ⊥ \left(\right. S A H \left.\right) \\ & B M \subset \left(\right. S B M \left.\right) \left.\right} \Rightarrow \left(\right. S A H \left.\right) ⊥ \left(\right. S B M \left.\right)\)

Ta có \(& \left(\right. S A H \left.\right) ⊥ \left(\right. S B M \left.\right) \\ & \left(\right. S A H \left.\right) \cap \left(\right. S B M \left.\right) = S H \\ & A K \subset \left(\right. S A H \left.\right) , A K ⊥ S H \left.\right} \Rightarrow A K ⊥ \left(\right. S B M \left.\right)\)

\(\Rightarrow d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = A K\)

Xét \(\Delta I A B\) có \(M D\) // \(A B \Rightarrow \frac{I D}{I A} = \frac{M D}{A B} = \frac{\frac{1}{2} C D}{A B} = \frac{1}{2}\)

\(\Rightarrow D\) là trung điểm của \(I A\) \(\Rightarrow I A = 2 A D = 2 a\).

\(\Delta A B I\) vuông tại \(A\) có \(A H\) là đường cao \(\Rightarrow \frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A I^{2}} = \frac{1}{a^{2}} + \frac{1}{4 a^{2}} = \frac{5}{4 a^{2}}\).

\(& S A ⊥ \left(\right. A B C D \left.\right) \\ & A H \subset \left(\right. A B C D \left.\right) \left.\right} \Rightarrow S A ⊥ A H\).

\(\Delta S A H\) vuông tại \(A\) có \(A K\) là đường cao \(\Rightarrow \frac{1}{A K^{2}} = \frac{1}{S A^{2}} + \frac{1}{A H^{2}} = \frac{1}{4 a^{2}} + \frac{5}{4 a^{2}} = \frac{6}{4 a^{2}}\)

\(\Rightarrow A K^{2} = \frac{4 a^{2}}{6}\)\(\Rightarrow A K = \frac{2 a}{\sqrt{6}} \Rightarrow d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = \frac{2 a}{\sqrt{6}}\).

\(\frac{d \left(\right. D , \left(\right. S B M \left.\right) \left.\right)}{d \left(\right. A , \left(\right. S B M \left.\right) \left.\right)} = \frac{D I}{A I} = \frac{1}{2}\)

\(\Rightarrow d \left(\right. D , \left(\right. S B M \left.\right) \left.\right) = \frac{1}{2} d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = \frac{a}{\sqrt{6}}\).

ĐK: {x>05x−m≥0{x>05x−m≥0 ⇔ {x>0x≥log5m{x>0x≥log5m (*)

Do m nguyên dương nên m ≥ 1 ⇒ log₅m ≥ 0.

Ta có: (2log23x−log3x−1)√5x−m=0(2log32⁡x−log3x−1)5x−m=0

⇔ ⎡⎢
⎢⎣log3x=1log3x=−125x=m[log3x=1log3x=−125x=m ⇔ ⎡⎢
⎢⎣x=3x=1√3x=log5m[x=3x=13x=log5m

TH1: m = 1 thì (*) là {x>0x≥0{x>0x≥0 ⇔ x > 0.

Mà m = 1 ⇒ x = log₅m = 0 (KTM) nên phương trình đã cho chỉ có hai nghiệm x₁ = 3 và x2=1√3.x2=13.

TH2: m > 1 thì (*) là {x>0x≥log5m{x>0x≥log5m ⇔ x ≥ log₅m.

Do đó phương trình đã cho chắc chắn có nghiệm x₁ = log₅m.

Do đó để phương trình có hai nghiệm phân biệt thì nó chỉ có thể nhận thêm một trong hai nghiệm x = 3 hoặc x=1√3.x=13.

+) Nếu 1√3>log5m13>log5m ⇒ 3 > log₅m nên cả hai nghiệm 3 và 1√313 đều thỏa mãn ĐK nên phương trình đã cho có 3 nghiệm (loại).

+) Nếu 1√3=log5m13=log5m ⇔ m=51√3∉Zm=513∉Z nên không xét trường hợp này.

+) Nếu 1√3<log5m13<log5m ⇔ m>51√3m>513 thì để phương trình đã cho có hai nghiệm phân biệt thì nghiệm x = 3 phải thỏa mãn 3 > log₅m ⇔ m < 5³ = 125.

Kết hợp m>51√3m>513 ta được 51√3<m<125.513<m<125.

Mà m ∈ ℤ nên m ∈ {3; 4;...; 124}.

Vậy m ∈ {1; 3; 4;...; 124} nên có 123 giá trị m thỏa mãn

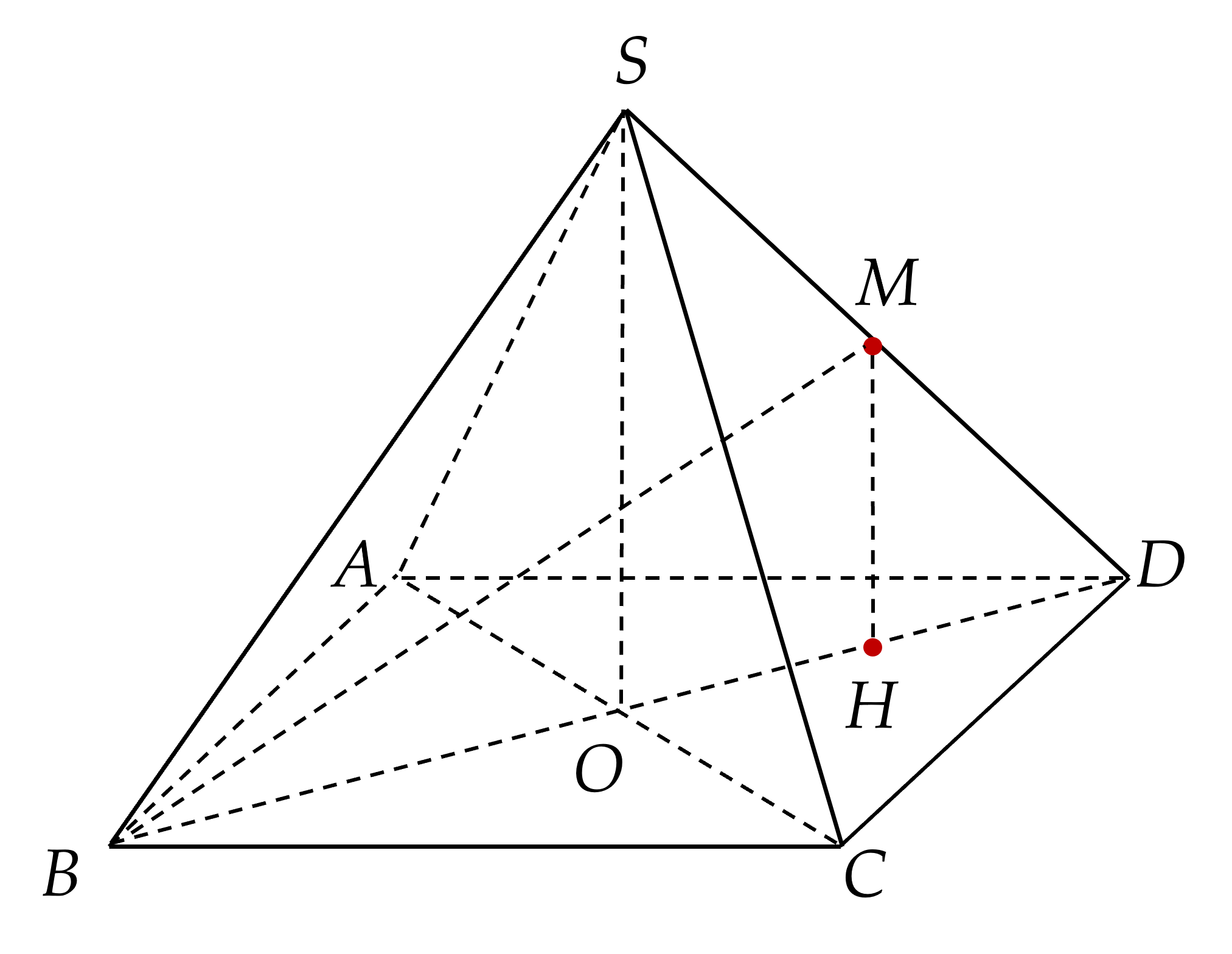
 Gọi \(O = A C \cap B D\)

\(\Rightarrow S O ⊥ \left(\right. A B C D \left.\right)\). Gọi \(H\) trung điểm của \(O D\).

Xét \(\Delta S O D\), \(M H\) là đường trung bình

\(\Rightarrow M H / / S O\) \(\Rightarrow M H ⊥ \left(\right. A B C D \left.\right)\).

Hình chiếu của đường thẳng \(B M\) trên mặt phẳng \(\left(\right. A B C D \left.\right)\) là \(B H\).

\(\Rightarrow \hat{\left(\right. B M ; \left(\right. A B C D \left.\right) \left.\right)} = \hat{\left(\right. B M ; B H \left.\right)} = \hat{M B H}\)

Xét tam giác vuông \(A B D\) có \(B D = \sqrt{A B^{2} + A D^{2}}\)\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} + \left(\left(\right. 2 a \left.\right)\right)^{2}}\)\(= 2 \sqrt{2} a\).

\(\Rightarrow B H = \frac{3}{4} B D = \frac{3 \sqrt{2} a}{2}\) và \(O D = \frac{1}{2} B D = \sqrt{2} a\).

Xét tam giác vuông \(S O D\) có:

\(S O = \sqrt{S D^{2} - O D^{2}}\)

\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} - \left(\left(\right. \sqrt{2} a \left.\right)\right)^{2}}\)

\(= \sqrt{2} a\).

\(\Rightarrow M H = \frac{1}{2} S O = \frac{\sqrt{2} a}{2}\).

Ta có: \(tan ⁡ \hat{M B H} = \frac{M H}{B H}\)

\(= \frac{\frac{a \sqrt{2}}{2}}{\frac{3 \sqrt{2} a}{2}}\)

\(= \frac{1}{3}\).

Gọi \(A\) là số tiền tối đa người này có thể vay, \(A_{i}\) là số tiền nợ sau tháng thứ \(i\). (đơn vị: triệu đồng)

\(r_{1} = \frac{5 \%}{12}\) là lãi suất/1 tháng, trong \(6\) tháng đầu

\(r_{2} = \frac{12 \%}{12} = 1 \%\) là lãi suất/1 tháng, từ tháng thứ 7 trở đi.

Sau 1 tháng, số tiền gốc và lãi là \(A \left(\right. 1 + r \left.\right)\), người đó trả \(15\) triệu nên còn nợ:

\(A_{1} = A \left(\right. 1 + r \left.\right) - 15\)

Sau tháng thứ 2:

\(A_{2} = A_{1} \left(\right. 1 + r_{1} \left.\right) - 15\)

\(= \left(\right. A \left(\right. 1 + r_{1} \left.\right) - 15 \left.\right) \left(\right. 1 + r_{1} \left.\right) - 15\)

\(= A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{2} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{2} - 1 \left]\right.\)

Sau tháng thứ 3:

\(A_{3} = A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{3} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{3} - 1 \left]\right.\)

…….

Sau tháng thứ 6:

\(A_{6} = A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - 1 \left]\right.\).

Sau tháng thứ 7: \(A_{7} = A_{6} \left(\right. 1 + r_{2} \left.\right) - 15\)

Sau tháng thứ 8: \(A_{8} = A_{6} \left(\left(\right. 1 + r_{2} \left.\right)\right)^{2} - \frac{15}{r_{2}} \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{2} - 1 \left]\right.\)

………

Sau tháng thứ 240 (sau đúng 20 năm):

\(A_{240} = A_{6} \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - \frac{15}{r_{2}} \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - 1 \left]\right.\)

Vì phải trả hết nợ sau 20 năm nên:

\(A_{240} = 0\)

\(\Leftrightarrow A_{6} = \frac{15 \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - 1 \left]\right.}{\left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} r_{2}} \approx 1 353 , 819328\)

\(\Rightarrow A = \frac{A_{6} + \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - 1 \left]\right.}{\left(\left(\right. 1 + r_{1} \left.\right)\right)^{6}} \approx 1 \overset{\cdot}{4} 09 , 163992\).

Vậy người này có thể mua được căn nhà có giá trị tối đa là \(\frac{A}{85 \%} \approx 1 657 , 83999\) triệu đồng \(\approx 1 , 65784\) tỷ đồng.