Câu 1. 

Phương thức biểu đạt chính: Nghị luận.

Câu 2. 

Luận đề: Nghịch cảnh giúp ta thành công.  

Câu 3. 

- Để làm sáng tỏ cho ý kiến: “nghịch cảnh thường giữ một chức vụ quan trọng trong sự thành công”, tác giả đã sử dụng những bằng chứng là: Voltaire, Marcel Proust, Ben Fortson, Milton, Beethoven, Charles Darwin, Hellen Keller, Rousseau.

- Nhận xét: Các bằng chứng đều là chuyện người thật việc thật kèm theo các chi tiết liên quan đến việc “vượt nghịch cảnh” để đạt thành công nên rất giàu tính thuyết phục.

Câu 4. 

- Mục đích: Thuyết phục người đọc rằng nghịch cảnh cũng có ý nghĩa quan trọng trong cuộc sống của mỗi người, đồng thời khích lệ người đọc không nản chí trước khó khăn.

- Nội dung: Qua văn bản, tác giả nhấn mạnh vai trò của nghịch cảnh trong việc rèn luyện ý chí, tôi luyện bản lĩnh; khích lệ con người nỗ lực vươn lên, không đầu hàng trước nghịch cảnh để đạt được thành công. 

Câu 5. 

Cách lập luận của tác giả trong văn bản rất chặt chẽ, thuyết phục vì tác giả đã đưa ra nhiều bằng chứng là chuyện người thật việc thật, có phân tích cụ thể trên nhiều lĩnh vực khác nhau và sử dụng những nhận định sắc sảo, giúp người đọc nhận ra giá trị đích thực của nghịch cảnh trong cuộc đời mỗi người. 

Ta có \(4^{x} - 3. 2^{x + 2} + m = 0 \Leftrightarrow 4^{x} - 12. 2^{x} + m = 0\) (1)

Đặt \(t = 2^{x} , \left(\right. t > 0 \left.\right)\) phương trình (1) trở thành \(t^{2} - 12 t + m = 0\) \(\left(\right. 2 \left.\right)\).

YCBT \(\Leftrightarrow \left(\right. 2 \left.\right)\) có hai nghiệm dương phân biệt \(t = t_{1} ; t = t_{2}\) và \(\log_2^{}t_1+\log_2^{}t_2=5^{}\)

\(\Leftrightarrow\begin{cases}\Delta^{^{\prime}}>0\\ S>0\\ P>0\\ t_1.t_2=32\end{cases}{}\)

\(\Leftrightarrow\begin{cases}36-m>0\\ m>0\\ m=32\end{cases}\)

\(\Leftrightarrow m = 32\).

\(\Delta S A B\) vuông tại \(A \Rightarrow S A ⊥ A B\).

\(\Delta S A D\) vuông tại \(A \Rightarrow S A ⊥ A D\).

Suy ra \(S A ⊥ \left(\right. A B C D \left.\right)\).

Gọi \(I\) là giao điểm của \(B M\) và \(A D\).

Dựng \(A H\) vuông góc với \(B M\) tại \(H\).

Dựng \(A K\) vuông góc với \(S H\) tại \(K\).

\(SA\bot\left(\right.ABCD\left.\right)\&BM\subset\left(\right.ABCD\left.\right)\left.\right.\Rightarrow SA\bot BM\) mà \(B M ⊥ A H\)

\(\Rightarrow B M ⊥ \left(\right. S A H \left.\right)\).

Ta có \(BM\bot\left(\right.SAH\left.\right)\&BM\subset\left(\right.SBM\left.\right)\left.\right.\Rightarrow\left(\right.SAH\left.\right)\bot\left(\right.SBM\left.\right)\)

Ta có \(\left(\right.SAH\left.\right)\bot\left(\right.SBM\left.\right),\left(\right.SAH\left.\right)\cap\left(\right.SBM\left.\right)=SH,AK\subset\left(\right.SAH\left.\right),AK\bot SH\left.\right.\Rightarrow AK\bot\left(\right.SBM\left.\right)\)

\(\Rightarrow d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = A K\)

Xét \(\Delta I A B\) có \(M D\) // \(A B \Rightarrow \frac{I D}{I A} = \frac{M D}{A B} = \frac{\frac{1}{2} C D}{A B} = \frac{1}{2}\)

\(\Rightarrow D\) là trung điểm của \(I A\) \(\Rightarrow I A = 2 A D = 2 a\).

\(\Delta A B I\) vuông tại \(A\) có \(A H\) là đường cao \(\Rightarrow \frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A I^{2}} = \frac{1}{a^{2}} + \frac{1}{4 a^{2}} = \frac{5}{4 a^{2}}\).

\(SA\bot\left(\right.ABCD\left.\right)\&AH\subset\left(\right.ABCD\left.\right)\left.\right.\Rightarrow SA\bot AH\).

\(\Delta S A H\) vuông tại \(A\) có \(A K\) là đường cao \(\Rightarrow \frac{1}{A K^{2}} = \frac{1}{S A^{2}} + \frac{1}{A H^{2}} = \frac{1}{4 a^{2}} + \frac{5}{4 a^{2}} = \frac{6}{4 a^{2}}\)

\(\Rightarrow A K^{2} = \frac{4 a^{2}}{6}\)\(\Rightarrow A K = \frac{2 a}{\sqrt{6}} \Rightarrow d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = \frac{2 a}{\sqrt{6}}\).

\(\frac{d \left(\right. D , \left(\right. S B M \left.\right) \left.\right)}{d \left(\right. A , \left(\right. S B M \left.\right) \left.\right)} = \frac{D I}{A I} = \frac{1}{2}\)

\(\Rightarrow d \left(\right. D , \left(\right. S B M \left.\right) \left.\right) = \frac{1}{2} d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = \frac{a}{\sqrt{6}}\)

Ta có: \(P\left(\right.A\left.\right)=0,2;P\left(\right.B\left.\right)=0,3;P\left(\overline{A}\overset{}{}\right)=0,8;P\left(\overline{B}\right)=0,7.\)

a) Gọi \(C\) là biến cố: "Lần bắn thứ nhất trúng bia, lần bắn thứ hai không trúng bia".

Ta có: \(C=\overline{A}B\) và \(\overline{A},B\) là hai biến cố độc lập

\(\Rightarrow P\left(C\left.\right)=P\left(\overline{A}\right).P\left(B\right)=0,8.0,3=0,24\right.\overset{}{}\)

b) Gọi biến cố \(D\): "Có ít nhất một lần bắn trúng bia".

Khi đó, biến cố \(\overline{D}\): "Cả hai lần bắn đều không trúng bia".

\(\rArr\overline{D}=AB\rArr P(\overline{D})=0,06\overset{}{}\)

\(\Rightarrow P\left(\right.D\left.\right)=1-P(\overline{D})=1-0,06=0,94\)

Điều kiện \(\begin{cases}x>0\\ 5^{x}-m\ge0\end{cases}\)

\(\Leftrightarrow\begin{cases}x>0\\ m\le5^{x}\end{cases}\)

\(\left(2^{}\log_3^2x-\log_3^{}x-1\right)\sqrt{5^{x}-m}=0\)

\(\lrArr\begin{cases}x>0,5^{x}-m\ge0\\ \left[\begin{array}{l}5^{x}-m=0\\ 2\log_3^2x-\log_3^{}x-1=0\end{array}\right.\end{cases}\)

\(\lrArr\begin{cases}\\ x>0,5^{x}-m\ge0\\ \left[\begin{array}{l}5^{x}-m=0\\ \log_3^{}x=\frac{-1}{2}\\ \log_3^{}x=1\end{array}\right.\end{cases}\begin{array}{l}\end{array}\)

\(\lrArr\begin{cases}x>0,5^{x}-m\ge0\\ \left[\begin{array}{l}x=\log_5^{}m\\ x=3^{\frac{1}{\sqrt2}}\\ x=3\end{array}\right.\\ \end{cases}\)

Khi \(m=1\implies x=\log_2^{}1=0\)

Vậy phương trình \(\left(\right.2log⁡_3^2x-log⁡_3x-1\left.\right)\sqrt{5^{x} - m}=0\) có 2 nghiệm \(\left[\begin{array}{l}x=3^{\frac{1}{\sqrt2}}\\ x=3\end{array}\right.\)

\(+m>1\implies x=\log_5^{}m\) là một nghiệm

Để phương trình có đúng 2 nghiệm thì \(\frac{1}{\sqrt3}\le\log_5^{}m<3\)

\(\Leftrightarrow 5^{\frac{1}{\sqrt{3}}} \leq m < 5^{3}\)

\(\Leftrightarrow 2 , 53 \leq m < 125\).

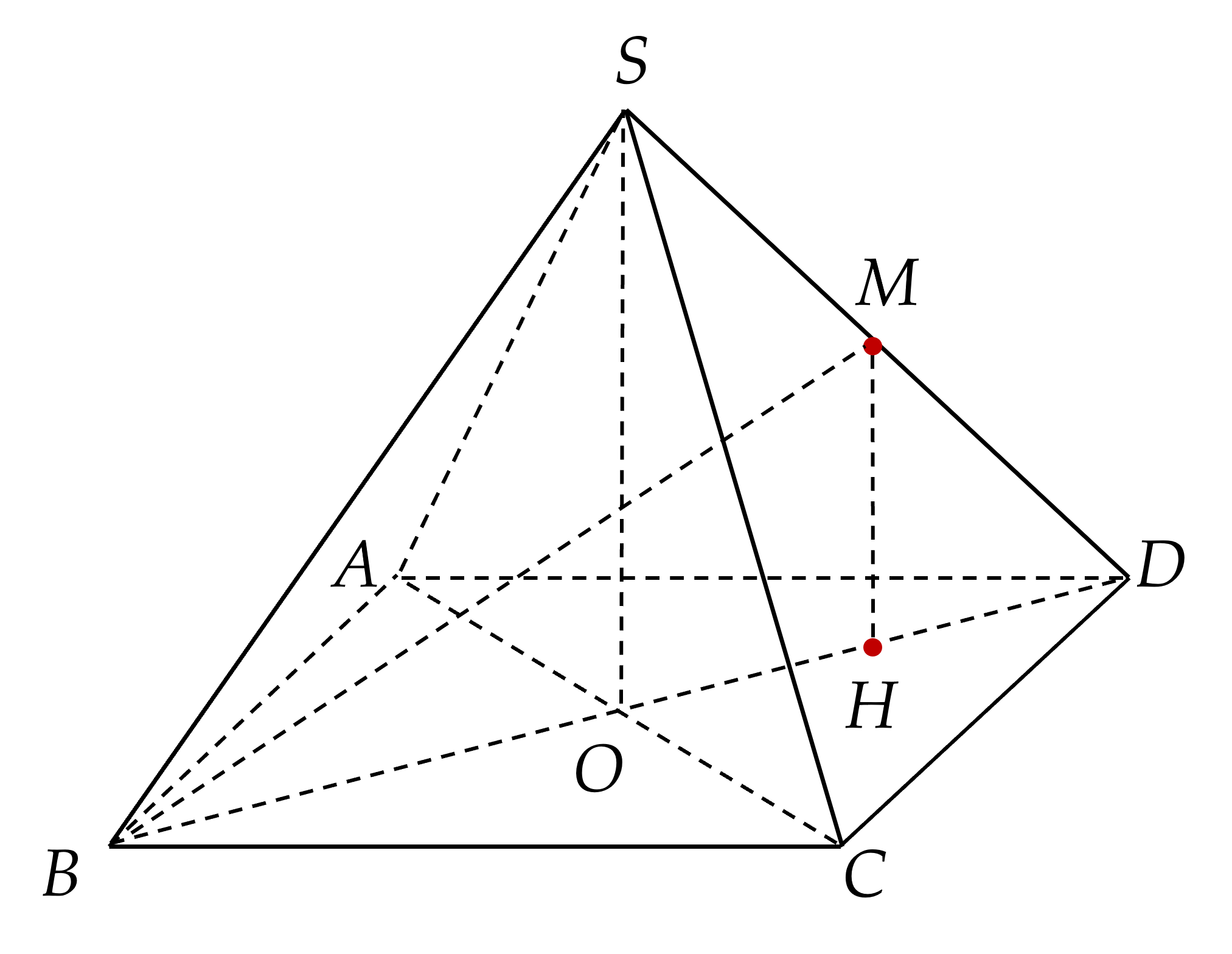
 Gọi \(O = A C \cap B D\)

\(\Rightarrow S O ⊥ \left(\right. A B C D \left.\right)\). Gọi \(H\) trung điểm của \(O D\).

Xét \(\Delta S O D\), \(M H\) là đường trung bình

\(\Rightarrow M H / / S O\) \(\Rightarrow M H ⊥ \left(\right. A B C D \left.\right)\).

Hình chiếu của đường thẳng \(B M\) trên mặt phẳng \(\left(\right. A B C D \left.\right)\) là \(B H\).

\(\Rightarrow \hat{\left(\right. B M ; \left(\right. A B C D \left.\right) \left.\right)} = \hat{\left(\right. B M ; B H \left.\right)} = \hat{M B H}\)

Xét tam giác vuông \(A B D\) có \(B D = \sqrt{A B^{2} + A D^{2}}\)\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} + \left(\left(\right. 2 a \left.\right)\right)^{2}}\)\(= 2 \sqrt{2} a\).

\(\Rightarrow B H = \frac{3}{4} B D = \frac{3 \sqrt{2} a}{2}\) và \(O D = \frac{1}{2} B D = \sqrt{2} a\).

Xét tam giác vuông \(S O D\) có:

\(S O = \sqrt{S D^{2} - O D^{2}}\)

\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} - \left(\left(\right. \sqrt{2} a \left.\right)\right)^{2}}\)

\(= \sqrt{2} a\).

\(\Rightarrow M H = \frac{1}{2} S O = \frac{\sqrt{2} a}{2}\).

Ta có: \(tan ⁡ \hat{M B H} = \frac{M H}{B H}\)

\(= \frac{\frac{a \sqrt{2}}{2}}{\frac{3 \sqrt{2} a}{2}}\)

\(= \frac{1}{3}\).

Gọi \(A\) là số tiền tối đa người này có thể vay, \(A_{i}\) là số tiền nợ sau tháng thứ \(i\). (đơn vị: triệu đồng)

\(r_{1} = \frac{5 \%}{12}\) là lãi suất/1 tháng, trong \(6\) tháng đầu

\(r_{2} = \frac{12 \%}{12} = 1 \%\) là lãi suất/1 tháng, từ tháng thứ 7 trở đi.

Sau 1 tháng, số tiền gốc và lãi là \(A \left(\right. 1 + r \left.\right)\), người đó trả \(15\) triệu nên còn nợ:

\(A_{1} = A \left(\right. 1 + r \left.\right) - 15\)

Sau tháng thứ 2:

\(A_{2} = A_{1} \left(\right. 1 + r_{1} \left.\right) - 15\)

\(= \left(\right. A \left(\right. 1 + r_{1} \left.\right) - 15 \left.\right) \left(\right. 1 + r_{1} \left.\right) - 15\)

\(= A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{2} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{2} - 1 \left]\right.\)

Sau tháng thứ 3:

\(A_{3} = A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{3} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{3} - 1 \left]\right.\)

…….

Sau tháng thứ 6:

\(A_{6} = A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - 1 \left]\right.\).

Sau tháng thứ 7: \(A_{7} = A_{6} \left(\right. 1 + r_{2} \left.\right) - 15\)

Sau tháng thứ 8: \(A_{8} = A_{6} \left(\left(\right. 1 + r_{2} \left.\right)\right)^{2} - \frac{15}{r_{2}} \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{2} - 1 \left]\right.\)

………

Sau tháng thứ 240 (sau đúng 20 năm):

\(A_{240} = A_{6} \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - \frac{15}{r_{2}} \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - 1 \left]\right.\)

Vì phải trả hết nợ sau 20 năm nên:

\(A_{240} = 0\)

\(\Leftrightarrow A_{6} = \frac{15 \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - 1 \left]\right.}{\left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} r_{2}} \approx 1 353 , 819328\)

\(\Rightarrow A = \frac{A_{6} + \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - 1 \left]\right.}{\left(\left(\right. 1 + r_{1} \left.\right)\right)^{6}} \approx 1 \overset{\cdot}{4} 09 , 163992\).

Vậy người này có thể mua được căn nhà có giá trị tối đa là \(\frac{A}{85 \%} \approx 1 657 , 83999\) triệu đồng \(\approx 1 , 65784\) tỷ đồng.

def should_swap(a, b):

if a % 2 != 0 and b % 2 == 0:

return True

elif a % 2 == b % 2 and a > b:

return True

else:

return False

def bubble_sort_chan_le(arr):

n = len(arr)

for i in range(n - 1):

for j in range(0, n - i - 1):

if should_swap(arr[j], arr[j + 1]):

arr[j], arr[j + 1] = arr[j + 1], arr[j]

my_list = [64, 34, 25, 12, 22, 11, 90]

bubble_sort_chan_le(my_list)

print("Mảng đã sắp xếp:", my_list)

Trình bày thuật toán

Bước 1. Nhập dãy số a[1], a[2], ..., a[n].

Bước 2. Tính tổng các phần tử của dãy số S = a[1] + a[2] + ... + a[n].

Bước 3. Kiểm tra nếu tổng S chia hết cho 2:

Bước 3.1. Nếu đúng, trả về "Tổng chẵn".

Bước 3.2. Nếu sai, trả về "Tổng lẻ".

[1] Chuyển mô tả thành chương trình bằng phương pháp làm mịn dần:

A = [int(input(f"Nhập phần tử thứ {i+1}: ")) for i in range(n)]

Tính tổng các phần tử của dãy số S = a[1] + a[2] + ... + a[n]. → Làm mịn tiếp tại [2]

if S%2 == 0:

return "Tổng chẵn"

else:

return "Tổng lẻ"

[2] Làm mịn chương trình tính tổng:

S = 0

Duyệt dãy từ i = 0 đến n: → Có thể chuyển trực tiếp thành câu lệnh

S = S + a[i]

[3] Chương trình hoàn chỉnh:

A = [int(input(f"Nhập phần tử thứ {i+1}: ")) for i in range(n)]

S = 0

Duyệt dãy từ i = 0 đến n: → Có thể chuyển trực tiếp thành câu lệnh

S = S + a[i]

if S%2 == 0:

return "Tổng chẵn"

else:

return "Tổng lẻ"

Kiểm thử giúp xác nhận rằng chương trình hoạt động đúng như yêu cầu và giúp phát hiện các lỗi trong mã nguồn hoặc lỗi logic mà có thể không được phát hiện trong quá trình lập trình. Từ đón đảm bảo rằng phần mềm hoạt động ổn định và có thể tin cậy trong mọi tình huống.

Ví dụ. Kiểm thử số nguyên tố:

- Với các số nguyên tố (ví dụ: 2, 3, 5, 7) thì chương trình trả về kết quả đúng.

- Với các số không phải là số nguyên tố (ví dụ: 4, 8, 9) thì kết quả trả về là sai.