Câu 1. (2.0 điểm) a. Xác định được yêu cầu về hình thức, dung lượng của đoạn văn - Xác định đúng yêu cầu về hình thức và dung lượng (khoảng 200 chữ) của đoạn văn. - Thí sinh có thể trình bày theo cách diễn dịch, quy nạp, tổng - phân - hợp, móc xích hoặc song hành. b. Xác định đúng vấn đề cần nghị luận Xác định đúng vấn đề cần nghị luận: Giải pháp giúp thế hệ trẻ hiện nay không chùn bước trước nghịch cảnh. c. Đề xuất được hệ thống ý phù hợp để làm rõ vấn đề nghị luận - Xác định được các ý phù hợp để làm rõ vấn đề nghị luận, sau đây là một số gợi ý: + Giải thích: Nghịch cảnh là những khó khăn, thử thách, trở ngại con người gặp phải trong cuộc sống. + Thực trạng: Trong cuộc sống hiện đại, thế hệ trẻ phải đối diện với nhiều khó khăn, thử thách như áp lực học tập, công việc, khủng hoảng tâm lý, tệ nạn xã hội, thiên tai, biến động kinh tế - xã hội,… + Nguyên nhân: Xã hội phát triển nhanh chóng kéo theo nhiều biến động phức tạp, tiềm ẩn nhiều rủi ro; thế hệ trẻ thiếu sự định hướng nên dễ trở nên vô định, bất lực khi đối diện với nghịch cảnh;… + Giải pháp: Rèn luyện ý chí, nghị lực để dũng cảm đối diện với nghịch cảnh; xây dựng tư duy tích cực; trang bị kiến thức, kĩ năng để đáp ứng được những yêu cầu về nhân lực của thị trường lao động; xây dựng mục tiêu rõ ràng để con đường chinh phục mục tiêu cụ thể, thuận lợi hơn; tìm kiếm sự hỗ trợ, chủ động chia sẻ với người thân để giải tỏa những áp lực về mặt tâm lí;… d. Viết đoạn văn đảm bảo các yêu cầu sau - Lựa chọn được các thao tác lập luận, phương thức biểu đạt phù hợp để triển khai vấn đề nghị luận. - Trình bày rõ quan điểm và hệ thống các ý. - Lập luận chặt chẽ, thuyết phục: Lí lẽ xác đáng, bằng chứng tiêu biểu, phù hợp; kết hợp nhuần nhuyễn giữa lí lẽ và bằng chứng. đ. Diễn đạt Đảm bảo chuẩn chính tả, dùng từ, ngữ pháp tiếng Việt, liên kết câu trong đoạn văn. e. Sáng tạo Thể hiện suy nghĩ sâu sắc về vấn đề nghị luận; có cách diễn đạt mới mẻ. Câu 2. (4.0 điểm) a. Xác định được yêu cầu của kiểu bài Xác định đúng yêu cầu của kiểu bài: Nghị luận văn học. b. Xác định đúng vấn đề cần nghị luận Xác định đúng vấn đề cần nghị luận: Phân tích những nét đặc sắc về nghệ thuật của bài thơ “Những dòng sông quê hương”. c. Đề xuất được hệ thống ý phù hợp để làm rõ vấn đề nghị luận - Xác định được các ý chính của bài viết. - Sắp xếp được các ý hợp lí theo bố cục 3 phần của bài văn nghị luận: * Mở bài: Giới thiệu vấn đề nghị luận và nêu khái quát quan điểm của cá nhân về vấn đề. * Thân bài: Triển khai vấn đề nghị luận: - Thể hiện quan điểm của người viết, có thể theo một số gợi ý sau: + Khái quát chung vài nét tiêu biểu về tác giả và tác phẩm. + Phân tích, đánh giá những nét đặc sắc về nghệ thuật của bài thơ: ++ Thể thơ: Tự do, không bị gò bó bởi quy tắc cụ thể về số câu, số chữ, dễ dàng biểu đạt cảm xúc. ++ Cấu tứ: Bài thơ được chia thành 4 khổ, mỗi khổ là một bức tranh riêng của sông quê, phản ánh những giai đoạn khác nhau trong cuộc đời của dòng sông. Cấu tứ này vừa giúp tác giả truyền tải một cách mạch lạc, rõ ràng về hình ảnh sông quê, vừa thể hiện được sự trôi chảy, luân hồi của dòng sông từ quá khứ, hiện tại đến tương lai, mang đậm tính biểu tượng về sự tiếp nối của truyền thống dân tộc. ++ Bố cục: Bài thơ có bố cục rõ ràng, từ hình ảnh sông gắn liền với cuộc sống nhân dân, đến những kí ức xưa, rồi quay về hiện thực cuộc sống hôm nay, kết thúc bằng hình ảnh mùa xuân tươi đẹp, đầy hi vọng. ++ Từ ngữ: Bài thơ sử dụng nhiều từ ngữ giàu giá trị gợi hình, gợi cảm như: “cuộn chảy”, “nguồn sống phù sa”, “mùa xuân tới”, “tiếng đoàn quân”,… => Ngôn ngữ thơ giản dị, gần gũi nhưng đầy sáng tạo và giàu sức gợi. ++ Hình ảnh “dòng sông quê hương” là hình ảnh trung tâm của bài thơ, gợi nhớ về những giá trị văn hóa, lịch sử và những kỉ niệm gắn bó với quê hương. Như vậy, hình ảnh sông không chỉ là một con sông bình thường mà mang ý nghĩa tượng trưng cho lịch sử, truyền thống của dân tộc. ++ Những hình ảnh như “chim bay theo dòng”, “dân vạn chài cười vang trên sóng” gợi lên không khí sống động, tràn đầy hi vọng, như một lời nhắc nhở về sự vĩnh hằng và sức sống mãnh liệt của quê hương. ++ Giọng điệu: Nhẹ nhàng, sâu lắng, chân thành thể hiện tình yêu sâu sắc mà tác giả dành cho quê hương, đất nước. Trong bài cũng có những đoạn thơ mang âm hưởng mạnh mẽ, đầy kiêu hãnh gợi lên sự trỗi dậy của những dòng sông. ++ Cách ngắt nhịp linh hoạt góp phần tạo nên nhạc tính cho bài thơ và thể hiện mạch cảm xúc của bài thơ. (HS có thể khai thác thêm những yếu tố khác dựa trên hiểu biết của bản thân, sao cho có kiến giải hợp lí, thuyết phục.) * Kết bài: Khái quát vấn đề nghị luận. d. Viết bài văn đảm bảo các yêu cầu sau - Lựa chọn được các thao tác lập luận, phương thức biểu đạt phù hợp để triển khai vấn đề nghị luận. - Trình bày rõ quan điểm và hệ thống các ý. - Lập luận chặt chẽ, thuyết phục: Lí lẽ xác đáng, bằng chứng tiêu biểu, phù hợp; kết hợp nhuần nhuyễn giữa lí lẽ và bằng chứng. đ. Diễn đạt Đảm bảo chuẩn chính tả, dùng từ, ngữ pháp tiếng Việt, liên kết văn bản. e. Sáng tạo Thể hiện suy nghĩ sâu sắc về vấn đề nghị luận; có cách diễn đạt mới mẻ.

Câu 1. Phương thức biểu đạt chính: Nghị luận. Câu 2. Luận đề: Nghịch cảnh giúp ta thành công. Câu 3. - Để làm sáng tỏ cho ý kiến: “nghịch cảnh thường giữ một chức vụ quan trọng trong sự thành công”, tác giả đã sử dụng những bằng chứng là: Voltaire, Marcel Proust, Ben Fortson, Milton, Beethoven, Charles Darwin, Hellen Keller, Rousseau. - Nhận xét: Các bằng chứng đều là chuyện người thật việc thật kèm theo các chi tiết liên quan đến việc “vượt nghịch cảnh” để đạt thành công nên rất giàu tính thuyết phục. Câu 4. - Mục đích: Thuyết phục người đọc rằng nghịch cảnh cũng có ý nghĩa quan trọng trong cuộc sống của mỗi người, đồng thời khích lệ người đọc không nản chí trước khó khăn. - Nội dung: Qua văn bản, tác giả nhấn mạnh vai trò của nghịch cảnh trong việc rèn luyện ý chí, tôi luyện bản lĩnh; khích lệ con người nỗ lực vươn lên, không đầu hàng trước nghịch cảnh để đạt được thành công. Câu 5. Cách lập luận của tác giả trong văn bản rất chặt chẽ, thuyết phục vì tác giả đã đưa ra nhiều bằng chứng là chuyện người thật việc thật, có phân tích cụ thể trên nhiều lĩnh vực khác nhau và sử dụng những nhận định sắc sảo, giúp người đọc nhận ra giá trị đích thực của nghịch cảnh trong cuộc đời mỗi người.

Ta có 4 x − 3. 2 x + 2 + m = 0 ⇔ 4 x − 12. 2 x + m = 0 4 x −3.2 x+2 +m=0⇔4 x −12.2 x +m=0 (1) Đặt t = 2 x , ( t > 0 ) t=2 x ,(t>0) phương trình (1) trở thành t 2 − 12 t + m = 0 t 2 −12t+m=0 ( 2 ) (2). YCBT ⇔ ( 2 ) ⇔(2) có hai nghiệm dương phân biệt t = t 1 ; t = t 2 t=t 1 ;t=t 2 và log ⁡ 2 t 1 + log ⁡ 2 t 2 = 5 log 2 t 1 +log 2 t 2 =5 ⇔ { Δ ′ > 0 S > 0 P > 0 t 1 . t 2 = 32 ⇔ ⎩ ⎨ ⎧ Δ ′ >0 S>0 P>0 t 1 .t 2 =32 ⇔ { 36 − m > 0 m > 0 m = 32 ⇔ ⎩ ⎨ ⎧ 36−m>0 m>0 m=32 ⇔ m = 32 ⇔m=32.

Ta có: P ( A ) = 0 , 2 ; P ( B ) = 0 , 3 ; P ( A ‾ ) = 0 , 8 ; P ( B ‾ ) = 0 , 7. P(A)=0,2;P(B)=0,3;P( A )=0,8;P( B )=0,7. a) Gọi C C là biến cố: "Lần bắn thứ nhất trúng bia, lần bắn thứ hai không trúng bia". Ta có: C = A ‾ B C= A B và A ‾ , B A ,B là hai biến cố độc lập ⇒ P ( C ) = P ( A ‾ ) . P ( B ) = 0 , 8.0 , 3 = 0 , 24. ⇒P(C)=P( A ).P(B)=0,8.0,3=0,24. b) Gọi biến cố D D: "Có ít nhất một lần bắn trúng bia". Khi đó, biến cố D ‾ D : "Cả hai lần bắn đều không trúng bia". ⇒ D ‾ = A B ⇒ P ( D ‾ ) = 0 , 06 ⇒ D =AB⇒P( D )=0,06 ⇒ P ( D ) = 1 − P ( D ‾ ) = 0 , 94. ⇒P(D)=1−P( D )=0,94.

\(\Delta S A B\) vuông tại \(A \Rightarrow S A ⊥ A B\).

\(\Delta S A D\) vuông tại \(A \Rightarrow S A ⊥ A D\).

Suy ra \(S A ⊥ \left(\right. A B C D \left.\right)\).

Gọi \(I\) là giao điểm của \(B M\) và \(A D\).

Dựng \(A H\) vuông góc với \(B M\) tại \(H\).

Dựng \(A K\) vuông góc với \(S H\) tại \(K\).

\(& S A ⊥ \left(\right. A B C D \left.\right) \\ & B M \subset \left(\right. A B C D \left.\right) \left.\right} \Rightarrow S A ⊥ B M\) mà \(B M ⊥ A H\)

\(\Rightarrow B M ⊥ \left(\right. S A H \left.\right)\).

Ta có \(& B M ⊥ \left(\right. S A H \left.\right) \\ & B M \subset \left(\right. S B M \left.\right) \left.\right} \Rightarrow \left(\right. S A H \left.\right) ⊥ \left(\right. S B M \left.\right)\)

Ta có \(& \left(\right. S A H \left.\right) ⊥ \left(\right. S B M \left.\right) \\ & \left(\right. S A H \left.\right) \cap \left(\right. S B M \left.\right) = S H \\ & A K \subset \left(\right. S A H \left.\right) , A K ⊥ S H \left.\right} \Rightarrow A K ⊥ \left(\right. S B M \left.\right)\)

\(\Rightarrow d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = A K\)

Xét \(\Delta I A B\) có \(M D\) // \(A B \Rightarrow \frac{I D}{I A} = \frac{M D}{A B} = \frac{\frac{1}{2} C D}{A B} = \frac{1}{2}\)

\(\Rightarrow D\) là trung điểm của \(I A\) \(\Rightarrow I A = 2 A D = 2 a\).

\(\Delta A B I\) vuông tại \(A\) có \(A H\) là đường cao \(\Rightarrow \frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A I^{2}} = \frac{1}{a^{2}} + \frac{1}{4 a^{2}} = \frac{5}{4 a^{2}}\).

\(& S A ⊥ \left(\right. A B C D \left.\right) \\ & A H \subset \left(\right. A B C D \left.\right) \left.\right} \Rightarrow S A ⊥ A H\).

\(\Delta S A H\) vuông tại \(A\) có \(A K\) là đường cao \(\Rightarrow \frac{1}{A K^{2}} = \frac{1}{S A^{2}} + \frac{1}{A H^{2}} = \frac{1}{4 a^{2}} + \frac{5}{4 a^{2}} = \frac{6}{4 a^{2}}\)

\(\Rightarrow A K^{2} = \frac{4 a^{2}}{6}\)\(\Rightarrow A K = \frac{2 a}{\sqrt{6}} \Rightarrow d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = \frac{2 a}{\sqrt{6}}\).

\(\frac{d \left(\right. D , \left(\right. S B M \left.\right) \left.\right)}{d \left(\right. A , \left(\right. S B M \left.\right) \left.\right)} = \frac{D I}{A I} = \frac{1}{2}\)

\(\Rightarrow d \left(\right. D , \left(\right. S B M \left.\right) \left.\right) = \frac{1}{2} d \left(\right. A , \left(\right. S B M \left.\right) \left.\right) = \frac{a}{\sqrt{6}}\).

Điều kiện \(\left{\right. & x > 0 \\ & 5^{x} - m \geq 0\)

\(\Leftrightarrow \left{\right. & x > 0 \\ & m \leq 5^{x}\).

(2log⁡32x−log⁡3x−1)5x−m=0(2log32​x−log3​x−1)5x−m​=0

⇔{x>0, 5x−m≥0[5x−m=02log⁡32x−log⁡3x−1=0⇔⎩⎨⎧​​x>0, 5x−m≥0[​5x−m=02log32​x−log3​x−1=0​​

⇔{x>0, 5x−m≥0[5x−m=0log⁡3x=−12log⁡3x=1⇔⎩⎨⎧​​x>0, 5x−m≥0​​5x−m=0log3​x=2−1​log3​x=1​​

⇔{x>0,5x−m≥0[x=log⁡5mx=312x=3⇔⎩⎨⎧​​x>0,5x−m≥0​​x=log5​mx=32​1​x=3​​

+ Khi m=1⇒x=log⁡21=0m=1⇒x=log2​1=0.

Vậy phương trình \(\left(\right. 2 \left(log ⁡\right)_{3}^{2} x - \left(log ⁡\right)_{3} x - 1 \left.\right) \sqrt{5^{x} - m} = 0\) có 2 nghiệm \(\left[\right. & x = 3^{\frac{1}{\sqrt{2}}} \\ & x = 3\)

+ m>1⇒x=log⁡5mm>1⇒x=log5​m là 1 nghiệm.

Để phương trình có đúng 2 nghiệm thì 13≤log⁡5m<33​1​≤log5​m<3

\(\Leftrightarrow 5^{\frac{1}{\sqrt{3}}} \leq m < 5^{3}\)

\(\Leftrightarrow 2 , 53 \leq m < 125\).

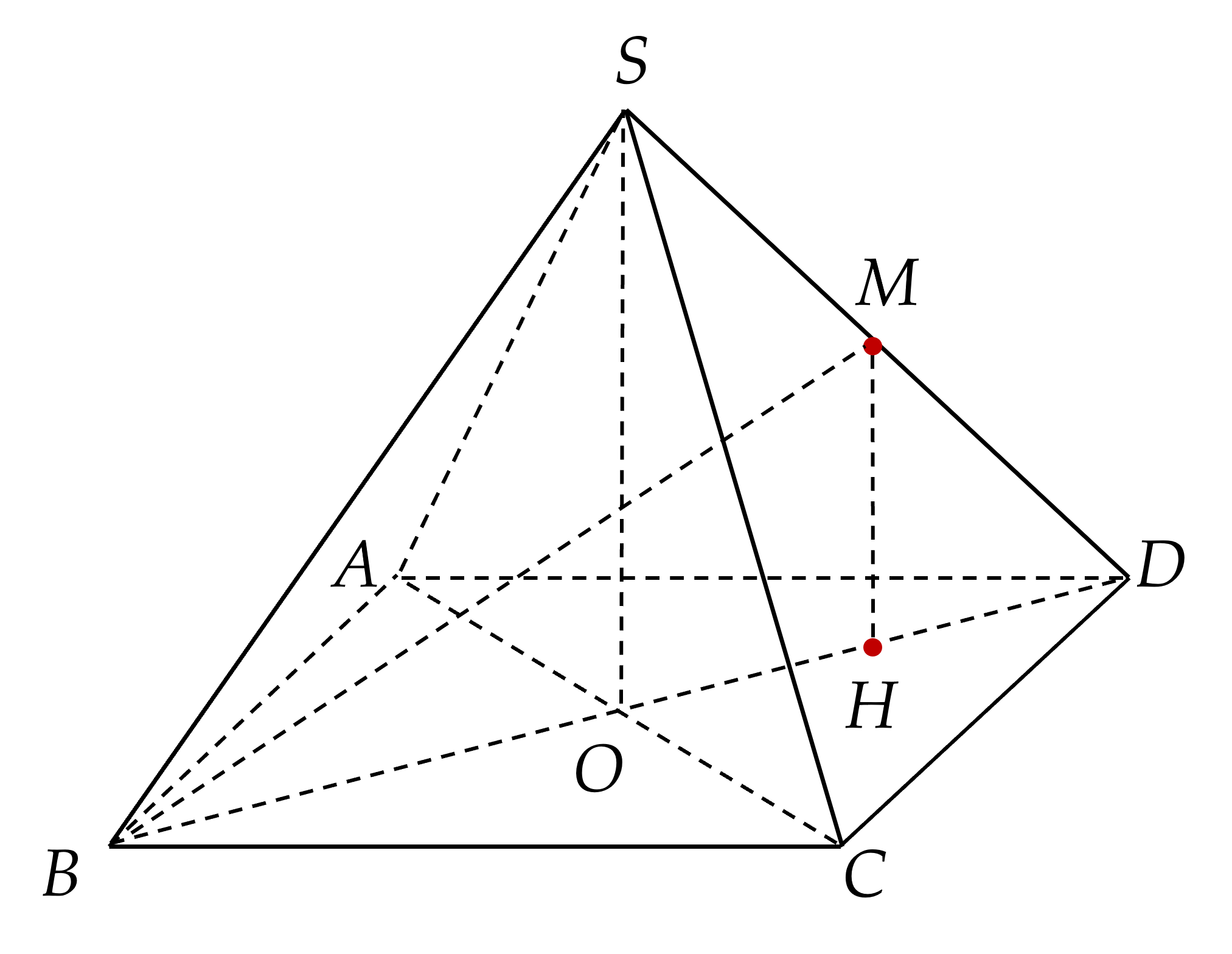
 Gọi \(O = A C \cap B D\)

\(\Rightarrow S O ⊥ \left(\right. A B C D \left.\right)\). Gọi \(H\) trung điểm của \(O D\).

Xét \(\Delta S O D\), \(M H\) là đường trung bình

\(\Rightarrow M H / / S O\) \(\Rightarrow M H ⊥ \left(\right. A B C D \left.\right)\).

Hình chiếu của đường thẳng \(B M\) trên mặt phẳng \(\left(\right. A B C D \left.\right)\) là \(B H\).

\(\Rightarrow \hat{\left(\right. B M ; \left(\right. A B C D \left.\right) \left.\right)} = \hat{\left(\right. B M ; B H \left.\right)} = \hat{M B H}\)

Xét tam giác vuông \(A B D\) có \(B D = \sqrt{A B^{2} + A D^{2}}\)\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} + \left(\left(\right. 2 a \left.\right)\right)^{2}}\)\(= 2 \sqrt{2} a\).

\(\Rightarrow B H = \frac{3}{4} B D = \frac{3 \sqrt{2} a}{2}\) và \(O D = \frac{1}{2} B D = \sqrt{2} a\).

Xét tam giác vuông \(S O D\) có:

\(S O = \sqrt{S D^{2} - O D^{2}}\)

\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} - \left(\left(\right. \sqrt{2} a \left.\right)\right)^{2}}\)

\(= \sqrt{2} a\).

\(\Rightarrow M H = \frac{1}{2} S O = \frac{\sqrt{2} a}{2}\).

Ta có: \(tan ⁡ \hat{M B H} = \frac{M H}{B H}\)

\(= \frac{\frac{a \sqrt{2}}{2}}{\frac{3 \sqrt{2} a}{2}}\)

\(= \frac{1}{3}\).

Gọi \(A\) là số tiền tối đa người này có thể vay, \(A_{i}\) là số tiền nợ sau tháng thứ \(i\). (đơn vị: triệu đồng)

\(r_{1} = \frac{5 \%}{12}\) là lãi suất/1 tháng, trong \(6\) tháng đầu

\(r_{2} = \frac{12 \%}{12} = 1 \%\) là lãi suất/1 tháng, từ tháng thứ 7 trở đi.

Sau 1 tháng, số tiền gốc và lãi là \(A \left(\right. 1 + r \left.\right)\), người đó trả \(15\) triệu nên còn nợ:

\(A_{1} = A \left(\right. 1 + r \left.\right) - 15\)

Sau tháng thứ 2:

\(A_{2} = A_{1} \left(\right. 1 + r_{1} \left.\right) - 15\)

\(= \left(\right. A \left(\right. 1 + r_{1} \left.\right) - 15 \left.\right) \left(\right. 1 + r_{1} \left.\right) - 15\)

\(= A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{2} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{2} - 1 \left]\right.\)

Sau tháng thứ 3:

\(A_{3} = A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{3} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{3} - 1 \left]\right.\)

…….

Sau tháng thứ 6:

\(A_{6} = A \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - 1 \left]\right.\).

Sau tháng thứ 7: \(A_{7} = A_{6} \left(\right. 1 + r_{2} \left.\right) - 15\)

Sau tháng thứ 8: \(A_{8} = A_{6} \left(\left(\right. 1 + r_{2} \left.\right)\right)^{2} - \frac{15}{r_{2}} \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{2} - 1 \left]\right.\)

………

Sau tháng thứ 240 (sau đúng 20 năm):

\(A_{240} = A_{6} \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - \frac{15}{r_{2}} \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - 1 \left]\right.\)

Vì phải trả hết nợ sau 20 năm nên:

\(A_{240} = 0\)

\(\Leftrightarrow A_{6} = \frac{15 \left[\right. \left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} - 1 \left]\right.}{\left(\left(\right. 1 + r_{2} \left.\right)\right)^{234} r_{2}} \approx 1 353 , 819328\)

\(\Rightarrow A = \frac{A_{6} + \frac{15}{r_{1}} \left[\right. \left(\left(\right. 1 + r_{1} \left.\right)\right)^{6} - 1 \left]\right.}{\left(\left(\right. 1 + r_{1} \left.\right)\right)^{6}} \approx 1 \overset{\cdot}{4} 09 , 163992\).

Vậy người này có thể mua được căn nhà có giá trị tối đa là \(\frac{A}{85 \%} \approx 1 657 , 83999\) triệu đồng \(\approx 1 , 65784\) tỷ đồng.

Kiểm thử giúp xác nhận rằng chương trình hoạt động đúng như yêu cầu và giúp phát hiện các lỗi trong mã nguồn hoặc lỗi logic mà có thể không được phát hiện trong quá trình lập trình. Từ đón đảm bảo rằng phần mềm hoạt động ổn định và có thể tin cậy trong mọi tình huống.

Ví dụ. Kiểm thử số nguyên tố:

- Với các số nguyên tố (ví dụ: 2, 3, 5, 7) thì chương trình trả về kết quả đúng.

- Với các số không phải là số nguyên tố (ví dụ: 4, 8, 9) thì kết quả trả về là sai.

Trình bày thuật toán

Bước 1. Nhập dãy số a[1], a[2], ..., a[n].

Bước 2. Tính tổng các phần tử của dãy số S = a[1] + a[2] + ... + a[n].

Bước 3. Kiểm tra nếu tổng S chia hết cho 2:

Bước 3.1. Nếu đúng, trả về "Tổng chẵn".

Bước 3.2. Nếu sai, trả về "Tổng lẻ".

[1] Chuyển mô tả thành chương trình bằng phương pháp làm mịn dần:

A = [int(input(f"Nhập phần tử thứ {i+1}: ")) for i in range(n)]

Tính tổng các phần tử của dãy số S = a[1] + a[2] + ... + a[n]. → Làm mịn tiếp tại [2]

if S%2 == 0:

return "Tổng chẵn"

else:

return "Tổng lẻ"

[2] Làm mịn chương trình tính tổng:

S = 0

Duyệt dãy từ i = 0 đến n: → Có thể chuyển trực tiếp thành câu lệnh

S = S + a[i]

[3] Chương trình hoàn chỉnh:

A = [int(input(f"Nhập phần tử thứ {i+1}: ")) for i in range(n)]

S = 0

Duyệt dãy từ i = 0 đến n: → Có thể chuyển trực tiếp thành câu lệnh

S = S + a[i]

if S%2 == 0:

return "Tổng chẵn"

else:

return "Tổng lẻ"