ĐK: {x>05x−m≥0{x>05x−m≥0 ⇔ {x>0x≥log5m{x>0x≥log5m (*)

Do m nguyên dương nên m ≥ 1 ⇒ log₅m ≥ 0.

Ta có: (2log23x−log3x−1)√5x−m=0(2log32⁡x−log3x−1)5x−m=0

⇔ ⎡⎢
⎢⎣log3x=1log3x=−125x=m[log3x=1log3x=−125x=m ⇔ ⎡⎢
⎢⎣x=3x=1√3x=log5m[x=3x=13x=log5m

TH1: m = 1 thì (*) là {x>0x≥0{x>0x≥0 ⇔ x > 0.

Mà m = 1 ⇒ x = log₅m = 0 (KTM) nên phương trình đã cho chỉ có hai nghiệm x₁ = 3 và x2=1√3.x2=13.

TH2: m > 1 thì (*) là {x>0x≥log5m{x>0x≥log5m ⇔ x ≥ log₅m.

Do đó phương trình đã cho chắc chắn có nghiệm x₁ = log₅m.

Do đó để phương trình có hai nghiệm phân biệt thì nó chỉ có thể nhận thêm một trong hai nghiệm x = 3 hoặc x=1√3.x=13.

+) Nếu 1√3>log5m13>log5m ⇒ 3 > log₅m nên cả hai nghiệm 3 và 1√313 đều thỏa mãn ĐK nên phương trình đã cho có 3 nghiệm (loại).

+) Nếu 1√3=log5m13=log5m ⇔ m=5x1√3∉Zm=5x1/căn3∉Z nên không xét trường hợp này.

+) Nếu 1√3<log5m13<log5m ⇔ m>5x1√3m>513 thì để phương trình đã cho có hai nghiệm phân biệt thì nghiệm x = 3 phải thỏa mãn 3 > log₅m ⇔ m < 5³ = 125.

Kết hợp m>51√3m>5x1/căn3 ta được 51√3<m<125.5x1/căn3<m<125.

Mà m ∈ ℤ nên m ∈ {3; 4;...; 124}.

Vậy m ∈ {1; 3; 4;...; 124} nên có 123 giá trị m thỏa mãn.

ĐK: {x>05x−m≥0{x>05x−m≥0 ⇔ {x>0x≥log5m{x>0x≥log5m (*)

Do m nguyên dương nên m ≥ 1 ⇒ log₅m ≥ 0.

Ta có: (2log23x−log3x−1)√5x−m=0(2log32⁡x−log3x−1)5x−m=0

⇔ ⎡⎢
⎢⎣log3x=1log3x=−125x=m[log3x=1log3x=−125x=m ⇔ ⎡⎢
⎢⎣x=3x=1√3x=log5m[x=3x=13x=log5m

TH1: m = 1 thì (*) là {x>0x≥0{x>0x≥0 ⇔ x > 0.

Mà m = 1 ⇒ x = log₅m = 0 (KTM) nên phương trình đã cho chỉ có hai nghiệm x₁ = 3 và x2=1√3.x2=13.

TH2: m > 1 thì (*) là {x>0x≥log5m{x>0x≥log5m ⇔ x ≥ log₅m.

Do đó phương trình đã cho chắc chắn có nghiệm x₁ = log₅m.

Do đó để phương trình có hai nghiệm phân biệt thì nó chỉ có thể nhận thêm một trong hai nghiệm x = 3 hoặc x=1√3.x=13.

+) Nếu 1√3>log5m13>log5m ⇒ 3 > log₅m nên cả hai nghiệm 3 và 1√313 đều thỏa mãn ĐK nên phương trình đã cho có 3 nghiệm (loại).

+) Nếu 1√3=log5m13=log5m ⇔ m=5x1√3∉Zm=5x1/căn3∉Z nên không xét trường hợp này.

+) Nếu 1√3<log5m13<log5m ⇔ m>5x1√3m>513 thì để phương trình đã cho có hai nghiệm phân biệt thì nghiệm x = 3 phải thỏa mãn 3 > log₅m ⇔ m < 5³ = 125.

Kết hợp m>51√3m>5x1/căn3 ta được 51√3<m<125.5x1/căn3<m<125.

Mà m ∈ ℤ nên m ∈ {3; 4;...; 124}.

Vậy m ∈ {1; 3; 4;...; 124} nên có 123 giá trị m thỏa mãn.

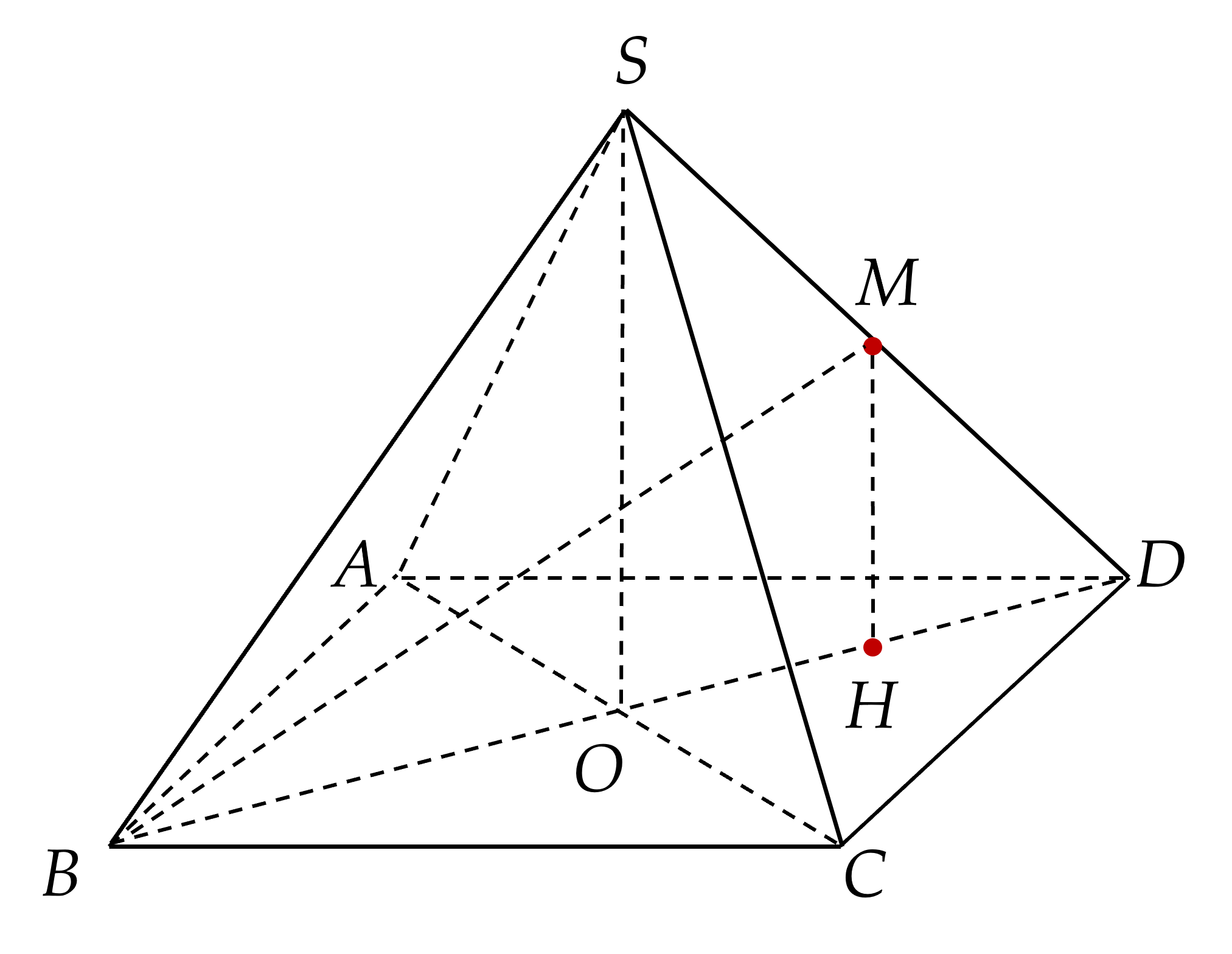 Gọi \(O = A C \cap B D\)

\(\Rightarrow S O ⊥ \left(\right. A B C D \left.\right)\). Gọi \(H\) trung điểm của \(O D\).

Xét \(\Delta S O D\), \(M H\) là đường trung bình

\(\Rightarrow M H / / S O\) \(\Rightarrow M H ⊥ \left(\right. A B C D \left.\right)\).

Hình chiếu của đường thẳng \(B M\) trên mặt phẳng \(\left(\right. A B C D \left.\right)\) là \(B H\).

\(\Rightarrow \hat{\left(\right. B M ; \left(\right. A B C D \left.\right) \left.\right)} = \hat{\left(\right. B M ; B H \left.\right)} = \hat{M B H}\)

Xét tam giác vuông \(A B D\) có \(B D = \sqrt{A B^{2} + A D^{2}}\)\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} + \left(\left(\right. 2 a \left.\right)\right)^{2}}\)\(= 2 \sqrt{2} a\).

\(\Rightarrow B H = \frac{3}{4} B D = \frac{3 \sqrt{2} a}{2}\) và \(O D = \frac{1}{2} B D = \sqrt{2} a\).

Xét tam giác vuông \(S O D\) có:

\(S O = \sqrt{S D^{2} - O D^{2}}\)

\(= \sqrt{\left(\left(\right. 2 a \left.\right)\right)^{2} - \left(\left(\right. \sqrt{2} a \left.\right)\right)^{2}}\)

\(= \sqrt{2} a\).

\(\Rightarrow M H = \frac{1}{2} S O = \frac{\sqrt{2} a}{2}\).

Ta có: \(tan ⁡ \hat{M B H} = \frac{M H}{B H}\)

\(= \frac{\frac{a \sqrt{2}}{2}}{\frac{3 \sqrt{2} a}{2}}\)

\(= \frac{1}{3}\).