Thuật toán giải phương trình bậc nhất ax + b = 0:

Bước 1. Nhập giá trị của a và b.

Bước 2. Kiểm tra nếu a = 0.

Nếu a = 0, kiểm tra nếu b = 0.

Nếu b = 0, phương trình có vô số nghiệm.

Nếu b ≠ 0, phương trình vô nghiệm.

Nếu a ≠ 0, tính x = -b/a.

Bước 3. Xuất giá trị của x.

Thuật toán giải phương trình bậc nhất ax + b = 0:

Bước 1. Nhập giá trị của a và b.

Bước 2. Kiểm tra nếu a = 0.

Nếu a = 0, kiểm tra nếu b = 0.

Nếu b = 0, phương trình có vô số nghiệm.

Nếu b ≠ 0, phương trình vô nghiệm.

Nếu a ≠ 0, tính x = -b/a.

Bước 3. Xuất giá trị của x.

Đầu vào: Số nguyên dương n.

Đầu ra: Tổng các số từ 1 đến n.

Các bước thực hiện:

Bước 1. Khởi tạo biến tong ← 0.

Bước 2. Khởi tạo biến i ← 1.

Bước 3. Trong khi i ≤ n:

tong ← tong + i

i ← i + 1

Bước 4. Trả về giá trị của biến tong.

Kết thúc thuật toán.

Trong qui trình nấu ăn, có thao tác: "Thêm một chút muối vào món ăn." Hướng dẫn này không rõ ràng vì "một chút" là một lượng không xác định. Mỗi người sẽ hiểu "một chút" theo một cách khác nhau, dẫn đến kết quả khác nhau.

Bài 1

Sử dụng phần mềm sơ đồ tư duy để tóm tắt về chủ đề "Cấu trúc lặp" đã học.

Hướng dẫn giải:

Dưới đây là các nội dung chính trong sơ đồ tư duy.

Trung tâm: Cấu trúc lặp

Định nghĩa:

+ Lặp lại một hoặc một nhóm câu lệnh nhiều lần.

+ Tiết kiệm thời gian và công sức khi viết code.

Phân loại:

- Lặp với số lần biết trước.

+ Số lần lặp được xác định trước.

+ Sử dụng biến đếm để theo dõi số lần lặp.

Lặp với số lần không biết trước.

+ Số lần lặp phụ thuộc vào một điều kiện.

+ Điều kiện được kiểm tra trước mỗi lần lặp hoặc sau mỗi lần lặp.

- Lưu ý:

+ Tránh vòng lặp vô hạn (điều kiện luôn đúng).

+ Sử dụng vòng lặp phù hợp với từng bài toán.

+ Tối ưu hóa vòng lặp để tăng hiệu suất.

Bài 1

Bài 1. (2 điểm) Thực hiện phép tính:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18}\);

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57\).

Hướng dẫn giải:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

Bài 2

Bài 2. (1,5 điểm). Biểu đồ cột kép dưới đây cho biết điểm trung bình (ĐTB) một số môn học: Văn, Toán, Anh, Khoa học tự nhiên (KHTN), Lịch sử và địa lí (LS&ĐL) trong học kì I (HKI) và học kì II (HKII) của bạn Minh như sau:

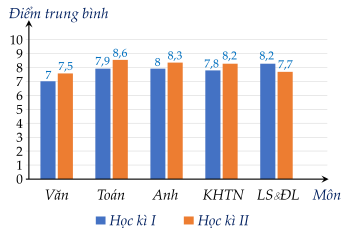
a) Môn học nào bạn Minh có điểm trung bình cao nhất học kì I.

b) Môn học nào bạn Minh có tiến bộ nhiều nhất.

c) Tính điểm trung bình (ĐTB) cả năm của môn Toán biết:

Điểm trung bình cả năm = (ĐTB HKI + 2 . ĐTB HKII) : 3

Hướng dẫn giải:

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

Bài 3

Bài 3. (2 điểm). Cho đoạn thẳng \(A B\) có độ dài \(5\) cm. Lấy điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) sao cho \(A C = 2 , 5\) cm.

a) Tính độ dài đoạn thẳng \(C B\).

b) Điểm \(C\) có là trung điểm của đoạn thẳng \(A B\) không? Vì sao?

Hướng dẫn giải:

a)

Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) nên:

\(A C + C B = A B\)

Thay \(A C = 2 , 5\) cm; \(A B = 5\) cm, ta có:

\(2 , 5 + C B = 5\)

\(C B = 5 - 2 , 5\)

\(C B = 2 , 5\) (cm).

b) Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) và \(A C = C B = 2 , 5\) cm.

Nên điểm \(C\) là trung điểm của đoạn thẳng \(A B\). 

Bài 1

Bài 1. (2 điểm) Thực hiện phép tính:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18}\);

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57\).

Hướng dẫn giải:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

Bài 2

Bài 2. (1,5 điểm). Biểu đồ cột kép dưới đây cho biết điểm trung bình (ĐTB) một số môn học: Văn, Toán, Anh, Khoa học tự nhiên (KHTN), Lịch sử và địa lí (LS&ĐL) trong học kì I (HKI) và học kì II (HKII) của bạn Minh như sau:

a) Môn học nào bạn Minh có điểm trung bình cao nhất học kì I.

b) Môn học nào bạn Minh có tiến bộ nhiều nhất.

c) Tính điểm trung bình (ĐTB) cả năm của môn Toán biết:

Điểm trung bình cả năm = (ĐTB HKI + 2 . ĐTB HKII) : 3

Hướng dẫn giải:

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

Bài 3

Bài 3. (2 điểm). Cho đoạn thẳng \(A B\) có độ dài \(5\) cm. Lấy điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) sao cho \(A C = 2 , 5\) cm.

a) Tính độ dài đoạn thẳng \(C B\).

b) Điểm \(C\) có là trung điểm của đoạn thẳng \(A B\) không? Vì sao?

Hướng dẫn giải:

a)

Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) nên:

\(A C + C B = A B\)

Thay \(A C = 2 , 5\) cm; \(A B = 5\) cm, ta có:

\(2 , 5 + C B = 5\)

\(C B = 5 - 2 , 5\)

\(C B = 2 , 5\) (cm).

b) Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) và \(A C = C B = 2 , 5\) cm.

Nên điểm \(C\) là trung điểm của đoạn thẳng \(A B\)

Bài 4

Bài 4. (1 điểm) Năm 2019, kim ngạch xuất khẩu của Việt Nam với thị trường châu Á là \(135 , 45\) tỉ USD, thị trường Châu Âu kém thị trường châu Á là \(88 , 18\) tỉ USD, còn thị trường châu Mỹ bằng \(156 , 32 \%\) thị trường châu Âu. Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là bao nhiêu? (Làm tròn đến hàng phần trăm)

Hướng dẫn giải:

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Âu là:

\(135 , 45 - 88 , 18 = 47 , 27\) (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Mỹ là:

\(47 , 27.156 , 32\) (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là:

\(135 , 45 - \left(\right. 47 , 27 + 73 , 89 \left.\right) = 14 , 29\) (tỉ USD).

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Âu là:

135,45−88,18=47,27 (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Mỹ là:

47,27.156,32 (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là:

135,45−(47,27+73,89)=14,29 (tỉ USD).

Bài 5

Bài 5. (0,5 điểm) Cho biểu thức \(A = \frac{1}{1.2} + \frac{1}{3.4} + \frac{1}{5.6} + \ldots + \frac{1}{49.50}\). Chứng minh rằng \(A < 1\).

Hướng dẫn giải:

Ta có:

\(A = \frac{1}{1.2} + \frac{1}{3.4} + \frac{1}{5.6} + . . . + \frac{1}{49.50}\)

\(A = \left(\right. 1 + \frac{1}{3} + \frac{1}{5} + . . . + \frac{1}{49} \left.\right) - \left(\right. \frac{1}{2} + \frac{1}{4} + . . . + \frac{1}{50} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{49} + \frac{1}{50} \left.\right) - 2 \left(\right. \frac{1}{2} + \frac{1}{4} + . . . + \frac{1}{50} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{49} + \frac{1}{50} \left.\right) - \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + . . . + \frac{1}{25} \left.\right)\)

\(A = \frac{1}{26} + \frac{1}{27} + . . . + \frac{1}{49} + \frac{1}{50} < \frac{1}{26} + \frac{1}{26} + \frac{1}{26} + . . . + \frac{1}{26} = \frac{25}{26} < 1.\)

Bài 1

Bài 1. (2 điểm) Thực hiện phép tính:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18}\);

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57\).

Hướng dẫn giải:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

Bài 2

Bài 2. (1,5 điểm). Biểu đồ cột kép dưới đây cho biết điểm trung bình (ĐTB) một số môn học: Văn, Toán, Anh, Khoa học tự nhiên (KHTN), Lịch sử và địa lí (LS&ĐL) trong học kì I (HKI) và học kì II (HKII) của bạn Minh như sau:

a) Môn học nào bạn Minh có điểm trung bình cao nhất học kì I.

b) Môn học nào bạn Minh có tiến bộ nhiều nhất.

c) Tính điểm trung bình (ĐTB) cả năm của môn Toán biết:

Điểm trung bình cả năm = (ĐTB HKI + 2 . ĐTB HKII) : 3

Hướng dẫn giải:

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

Bài 3

Bài 3. (2 điểm). Cho đoạn thẳng \(A B\) có độ dài \(5\) cm. Lấy điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) sao cho \(A C = 2 , 5\) cm.

a) Tính độ dài đoạn thẳng \(C B\).

b) Điểm \(C\) có là trung điểm của đoạn thẳng \(A B\) không? Vì sao?

Hướng dẫn giải:

a)

Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) nên:

\(A C + C B = A B\)

Thay \(A C = 2 , 5\) cm; \(A B = 5\) cm, ta có:

\(2 , 5 + C B = 5\)

\(C B = 5 - 2 , 5\)

\(C B = 2 , 5\) (cm).

b) Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) và \(A C = C B = 2 , 5\) cm.

Nên điểm \(C\) là trung điểm của đoạn thẳng \(A B\). 

Bài 1

Bài 1. (2 điểm) Thực hiện phép tính:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18}\);

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57\).

Hướng dẫn giải:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

Bài 2

Bài 2. (1,5 điểm). Biểu đồ cột kép dưới đây cho biết điểm trung bình (ĐTB) một số môn học: Văn, Toán, Anh, Khoa học tự nhiên (KHTN), Lịch sử và địa lí (LS&ĐL) trong học kì I (HKI) và học kì II (HKII) của bạn Minh như sau:

a) Môn học nào bạn Minh có điểm trung bình cao nhất học kì I.

b) Môn học nào bạn Minh có tiến bộ nhiều nhất.

c) Tính điểm trung bình (ĐTB) cả năm của môn Toán biết:

Điểm trung bình cả năm = (ĐTB HKI + 2 . ĐTB HKII) : 3

Hướng dẫn giải:

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

Bài 3

Bài 3. (2 điểm). Cho đoạn thẳng \(A B\) có độ dài \(5\) cm. Lấy điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) sao cho \(A C = 2 , 5\) cm.

a) Tính độ dài đoạn thẳng \(C B\).

b) Điểm \(C\) có là trung điểm của đoạn thẳng \(A B\) không? Vì sao?

Hướng dẫn giải:

a)

Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) nên:

\(A C + C B = A B\)

Thay \(A C = 2 , 5\) cm; \(A B = 5\) cm, ta có:

\(2 , 5 + C B = 5\)

\(C B = 5 - 2 , 5\)

\(C B = 2 , 5\) (cm).

b) Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) và \(A C = C B = 2 , 5\) cm.

Nên điểm \(C\) là trung điểm của đoạn thẳng \(A B\)

Bài 4

Bài 4. (1 điểm) Năm 2019, kim ngạch xuất khẩu của Việt Nam với thị trường châu Á là \(135 , 45\) tỉ USD, thị trường Châu Âu kém thị trường châu Á là \(88 , 18\) tỉ USD, còn thị trường châu Mỹ bằng \(156 , 32 \%\) thị trường châu Âu. Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là bao nhiêu? (Làm tròn đến hàng phần trăm)

Hướng dẫn giải:

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Âu là:

\(135 , 45 - 88 , 18 = 47 , 27\) (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Mỹ là:

\(47 , 27.156 , 32\) (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là:

\(135 , 45 - \left(\right. 47 , 27 + 73 , 89 \left.\right) = 14 , 29\) (tỉ USD).

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Âu là:

135,45−88,18=47,27 (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Mỹ là:

47,27.156,32 (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là:

135,45−(47,27+73,89)=14,29 (tỉ USD).

Bài 5

Bài 5. (0,5 điểm) Cho biểu thức \(A = \frac{1}{1.2} + \frac{1}{3.4} + \frac{1}{5.6} + \ldots + \frac{1}{49.50}\). Chứng minh rằng \(A < 1\).

Hướng dẫn giải:

Ta có:

\(A = \frac{1}{1.2} + \frac{1}{3.4} + \frac{1}{5.6} + . . . + \frac{1}{49.50}\)

\(A = \left(\right. 1 + \frac{1}{3} + \frac{1}{5} + . . . + \frac{1}{49} \left.\right) - \left(\right. \frac{1}{2} + \frac{1}{4} + . . . + \frac{1}{50} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{49} + \frac{1}{50} \left.\right) - 2 \left(\right. \frac{1}{2} + \frac{1}{4} + . . . + \frac{1}{50} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{49} + \frac{1}{50} \left.\right) - \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + . . . + \frac{1}{25} \left.\right)\)

\(A = \frac{1}{26} + \frac{1}{27} + . . . + \frac{1}{49} + \frac{1}{50} < \frac{1}{26} + \frac{1}{26} + \frac{1}{26} + . . . + \frac{1}{26} = \frac{25}{26} < 1.\)

Bài 1

Bài 1. (2 điểm) Thực hiện phép tính:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18}\);

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57\).

Hướng dẫn giải:

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

Bài 2

Bài 2. (1,5 điểm). Biểu đồ cột kép dưới đây cho biết điểm trung bình (ĐTB) một số môn học: Văn, Toán, Anh, Khoa học tự nhiên (KHTN), Lịch sử và địa lí (LS&ĐL) trong học kì I (HKI) và học kì II (HKII) của bạn Minh như sau:

a) Môn học nào bạn Minh có điểm trung bình cao nhất học kì I.

b) Môn học nào bạn Minh có tiến bộ nhiều nhất.

c) Tính điểm trung bình (ĐTB) cả năm của môn Toán biết:

Điểm trung bình cả năm = (ĐTB HKI + 2 . ĐTB HKII) : 3

Hướng dẫn giải:

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

Bài 3

Bài 3. (2 điểm). Cho đoạn thẳng \(A B\) có độ dài \(5\) cm. Lấy điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) sao cho \(A C = 2 , 5\) cm.

a) Tính độ dài đoạn thẳng \(C B\).

b) Điểm \(C\) có là trung điểm của đoạn thẳng \(A B\) không? Vì sao?

Hướng dẫn giải:

a)

Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) nên:

\(A C + C B = A B\)

Thay \(A C = 2 , 5\) cm; \(A B = 5\) cm, ta có:

\(2 , 5 + C B = 5\)

\(C B = 5 - 2 , 5\)

\(C B = 2 , 5\) (cm).

b) Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) và \(A C = C B = 2 , 5\) cm.

Nên điểm \(C\) là trung điểm của đoạn thẳng \(A B\)

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)