a) \(\frac{1}{2} - \frac{1}{2} : x = \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{1}{2} - \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{- 1}{4}\)

\(x = \frac{1}{2} : \&\text{nbsp}; \frac{- 1}{4}\)

\(x = - 2\)

b) \(\frac{x - 1}{15} = \frac{3}{5}\)

\(\frac{x - 1}{15} = \frac{9}{15}\)

\(x - 1 = 9\)

\(x = 10\)

c) \(x + 2 , 5 = 1 , 4\)

\(x = 1 , 4 - 2 , 5\)

\(x = - 1 , 1\)

a) \(A = 2 , 34 + 5 , 35 + 7 , 66 + 4 , 65\)

\(= \left(\right. 2 , 34 + 7 , 66 \left.\right) + \left(\right. 4 , 65 + 5 , 35 \left.\right)\)

\(= 10 + 10\)

\(= 20\)

b) \(B = 2 , 13.75 + 2 , 13.25\)

\(= 2 , 13. \left(\right. 75 + 25 \left.\right)\)

\(= 2 , 13.100\)

\(= 213\)

c) \(C = \frac{1}{3} - \frac{1}{3} : \frac{3}{4}\)

\(= \frac{1}{3} - \frac{1}{3} . \&\text{nbsp}; \frac{4}{3}\)

\(= \frac{1}{3} - \frac{4}{9}\)

\(= \frac{3}{9} - \frac{4}{9}\)

\(= \frac{- 1}{9}\)

a) Các tia chung gốc \(A\) là:

   \(A B\) (hay \(A y\)); \(A M\) (hay \(A C\), \(A z\)); \(A x\).

b) Các điểm thuộc tia \(A z\) mà không thuộc tia \(A y\) là:

   \(M\) và \(C\).

c) Tia \(A M\) và tia \(M A\) không chung gốc nên không phải hai tia đối nhau.

Số tiền \(15\) quyển vở trước khi giảm giá là:

\(15.7\) \(000 = 105\) \(000\) (đồng)

Số tiền \(15\) quyển vở sau khi giàm giá \(10 \%\) là:

\(105\) \(000.90 \% = 94\) \(500\) (đồng)

Vậy bạn An đem theo \(100\) \(000\) đồng nên đủ tiền mua \(15\) quyển vở.

a) \(1 - \frac{1}{2} + \frac{1}{3} = \frac{6 - 3 + 2}{6} = \frac{5}{6}\).

b) \(\frac{2}{5} + \frac{3}{5} : \frac{9}{10} = \frac{2}{5} + \frac{3}{5} \cdot \frac{10}{9} = \frac{2}{5} + \frac{2}{3} = \frac{16}{15}\).

c) \(\frac{7}{11} \cdot \frac{3}{4} + \frac{7}{11} \cdot \frac{1}{4} + \frac{4}{11} = \frac{7}{11} \left(\right. \frac{3}{4} + \frac{1}{4} \left.\right) + \frac{4}{11} = \frac{7}{11} + \frac{4}{11} = 1\).

d) \(\left(\right. \frac{3}{4} + 0 , 5 + 25 \% \left.\right) \cdot 2 \frac{2}{3} = \left(\right. \frac{3}{4} + \frac{1}{2} + \frac{1}{4} \left.\right) \cdot \frac{8}{3} = \frac{3}{2} \cdot \frac{8}{3} = 4\).

​Thuật toán có cấu trúc lặp dùng để mô tả các bước của việc lặp lại quá trình kiểm tra số lượng vở trong cặp nhiều lần. Vì vậy em phải sử dụng sơ đồ khối mô tả cấu trúc lặp đó.

Em có thể tham khảo sơ đồ sau đây:

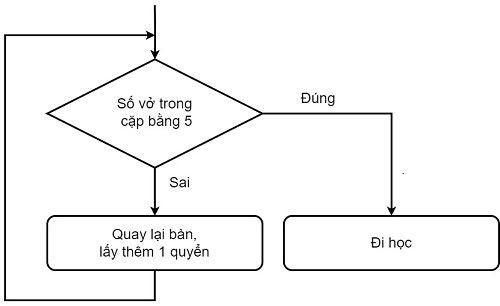
​Thuật toán có cấu trúc lặp dùng để mô tả các bước của việc lặp lại quá trình kiểm tra số lượng vở trong cặp nhiều lần. Vì vậy em phải sử dụng sơ đồ khối mô tả cấu trúc lặp đó.

Em có thể tham khảo sơ đồ sau đây:

Cấu trúc rẽ nhánh dạng đủ có dạng:

1. - Kiểm tra một điều kiện.
2. - Nếu điều kiện đúng thì thực hiện nhiệm vụ 1.
3. - Nếu điều kiện sai thì thực hiện nhiệm vụ 2.​

Ví dụ:

Nếu như hôm nay là thứ 7 hoặc CN thì Hoàng ở nhà, nếu không thì Hoàng đi học.

Trong ví dụ trên ta có thể thấy:

1. - Điều kiện kiểm tra: Hôm nay là thứ mấy?
2. - Nếu điều kiện hôm nay là thứ 7 hoặc CN đúng thì thực hiện nhiệm vụ 1: Hoàng ở nhà.
3. - Nếu điều kiện hôm nay là thứ 7 hoặc CN sai thì thực hiện nhiệm vụ 2: Hoàng đi học

Tác hại, nguy cơ khi dùng Internet:

1. - Thông tin cá nhân bị lộ hoặc bị đánh cắp.
2. - Máy tính bị nhiễm virus hay mã độc.
3. - Bị lừa đảo, dụ dỗ, đe dọa, bắt nạt trên mạng.
4. - Tiếp nhận thông tin không chính xác.
5. - Nghiện Internet, nghiện trò chơi trên mạng.

Quy tắc an toàn khi sử dụng Internet

1. - Giữ an toàn.
2. - Không gặp gỡ.
3. - Đừng chấp nhận.
4. - Kiểm tra độ tin cậy.
5. - Hãy nói ra.

Thuật toán giải phương trình bậc nhất ax + b = 0:

Bước 1. Nhập giá trị của a và b.

Bước 2. Kiểm tra nếu a = 0.

Nếu a = 0, kiểm tra nếu b = 0.

Nếu b = 0, phương trình có vô số nghiệm.

Nếu b ≠ 0, phương trình vô nghiệm.

Nếu a ≠ 0, tính x = -b/a.

Bước 3. Xuất giá trị của x.