

Trần Hương Thảo
Giới thiệu về bản thân



































Gọi số gà cần bổ sung là \(x\) (con) (\(x \in \mathbb{N}\))
Tổng số gà sau khi bổ sung: \(100 + x\) (con)
Sản lượng trung bình mỗi con: \(250 - 2 x\) (quả)
Tổng số trứng: \(\left(\right. 100 + x \left.\right) \left(\right. 250 - 2 x \left.\right)\) (quả)
Doanh thu: \(R \left(\right. x \left.\right) = 3 000. \left(\right. 100 + x \left.\right) \left(\right. 250 - 2 x \left.\right)\) (đồng)
Ta có:
\(T \left(\right. x \left.\right) = \left(\right. 100 + x \left.\right) \left(\right. 250 - 2 x \left.\right)\)
\(= - 2 x^{2} + 50 x + 25 000\)
\(= - 2 \left(\right. x - \frac{25}{2} \left.\right)^{2} + 25 312 , 5\)
Để doanh thu \(R \left(\right. x \left.\right)\) lớn nhất thì \(T \left(\right. x \left.\right)\) phải đạt giá trị lớn nhất.
Để \(T \left(\right. x \left.\right)\) phải đạt giá trị lớn nhất khi và chỉ khi \(\left(\right. x - \frac{25}{2} \left.\right)^{2}\) đạt giá trị nhỏ nhất với \(x\) là số tự nhiên, \(x\) nhỏ nhất.
Suy ra tìm được \(x = 12.\)
Vậy số gà ít nhất cần bổ sung để đạt doanh thu cao nhất là \(12\) con.
Vậy doanh thu tối đa là: \(R \left(\right. 12 \left.\right) = 3 000. \left(\right. 100 + 12 \left.\right) \left(\right. 250 - 2.12 \left.\right) = 75 936 000\) đồng
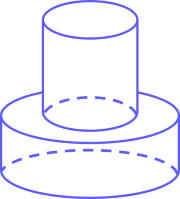
Thể tích khối \(\left(\right. H_{1} \left.\right)\) là \(V_{1} = \pi . r_{1}^{2} . h_{1}\)
Thể tích khối \(\left(\right. H_{2} \left.\right)\) là \(V_{2} = \pi . r_{2}^{2} . h_{2} = \pi . \frac{1}{4} . r_{1}^{2} . 2. h_{1} = \frac{1}{2} . \pi . r_{1}^{2} . h_{1} = \frac{1}{2} V_{1}\)
Mà \(V_{1} + V_{2} = 30\)
\(V_{1} + \frac{1}{2} V_{1} = 30\)
\(V_{1} = 20\) (cm3).
Vậy thể tích khối \(\left(\right. H_{1} \left.\right)\) là \(20\) cm3.

a) Gọi \(I\) là trung điểm của \(H B\)
Suy ra \(H I = I B = \frac{H B}{2}\)
Xét nửa đường tròn \(\left(\right. O \left.\right)\), đường kính \(A B\) có: \(\hat{A C B} = 9 0^{\circ}\) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(\Delta C H B\) vuông, mà \(C I\) là đường trung tuyến ứng với cạnh huyền
Suy ra \(I C = I H = I B = \frac{H B}{2}\) (1)
Vì \(K\) là hình chiếu của \(H\) trên \(A B\) nên \(\hat{H K B} = 9 0^{\circ}\)
Suy ra \(\Delta K H B\) vuông, mà \(K I\) là đường trung tuyến ứng với cạnh huyền
Suy ra \(I K = I H = I B = \frac{H B}{2}\) (2)
Từ (1) và (2) suy ra \(I C = I K = I H = I B\).
Vậy bốn điểm \(C\), \(B\), \(H\), \(K\) cùng thuộc một đường tròn.
b) Có \(\hat{M C A} = \hat{M B A}\) (góc nội tiếp cùng chắn cung \(A M\))
\(\hat{A C K} = \hat{M B A}\) (tứ giác \(C H K B\) nội tiếp)
Suy ra \(\hat{M C A} = \hat{A C K}\)
Suy ra \(C A\) là phân giác \(\hat{M C K}\)
c) Theo giả thiết: \(\frac{A P . M B}{M A} = R\)
Suy ra \(\frac{A P}{M A} = \frac{O A}{M B}\)
Xét \(\Delta P A O\) và \(\Delta A M B\) có:
\(\frac{A P}{M A} = \frac{O A}{M B}\);
\(\hat{P A O} = \hat{A M B} = 9 0^{\circ}\)
Suy ra \(\Delta P A O \sim \Delta A M B\) (c.g.c)
\(\hat{P O A} = \hat{M B A}\) (hai góc tương ứng)
Suy ra \(O P\) // \(B Q\).
Xét \(\Delta A B O\) có: \(O P\) // \(B O\), \(O\) là trung điểm của \(A B\) nên \(P\) là trung điểm của \(A Q\).
Xét \(\Delta A B P\) có: \(F K\) // \(A P\) nên \(\frac{F K}{A P} = \frac{B F}{B P}\)
Xét \(\Delta A B P\) có: \(F K\) // \(A P\) nên \(\frac{F H}{Q P} = \frac{B F}{B P}\)
Từ đó suy ra \(H K = F K\) hay \(P B\) đi qua trung điểm của đoạn thẳng \(H K\).
Đổi \(30\) phút \(= \frac{1}{2}\) giờ;
Ca nô đi hết \(10\) giờ \(36\) phút - \(6\) giờ \(30\) phút = \(4\) giờ \(6\) phút \(= \frac{41}{10}\) giờ.
Gọi vận tốc riêng của ca nô là \(x\) (đơn vị: km/h) \(\left(\right. x > 3 \left.\right)\)
Vận tốc ca nô đi xuôi dòng là \(x + 3\) (km/h)
Vận tốc ca nô đi ngược dòng là \(x - 3\) (km/h)
Thời gian ca nô đi xuôi dòng là \(\frac{48}{x + 3}\) (h)
Thời gian ca nô đi ngược dòng là \(\frac{48}{x - 3}\) (h)
Theo đề bài ta có phương trình \(\frac{48}{x + 3} + \frac{1}{2} + \frac{48}{x - 3} = \frac{41}{10}\)
\(\frac{48}{x + 3} + \frac{48}{x - 3} = \frac{18}{5}\)
\(\frac{48 \left(\right. x - 3 \left.\right) + 48 \left(\right. x + 3 \left.\right)}{\left(\right. x - 3 \left.\right) \left(\right. x + 3 \left.\right)} = \frac{18}{5}\)
\(\frac{96 x}{\left(\right. x - 3 \left.\right) \left(\right. x + 3 \left.\right)} = \frac{18}{5}\)
\(3 x^{2} - 80 x - 27 = 0\)
\(x = \frac{- 1}{3}\) (không thỏa mãn) hoặc \(x = 27\) (thỏa mãn).
Vậy vận tốc riêng của ca nô là \(27\) km/h.
1. Tổng số học sinh là 2+5+12+18+3=40
Tần số của nhóm [6;8) lÀ 18 Tần số tương đối của nhóm [6;8) là 18/4 = 0,45
2. Các số nguyên tố từ 1 dến 5 là 2,3,5,7,11,13 Có 6 số nguyên tố
Xcá suất của biến cố M là 6/15 = 2/5 = 0,4