Hướng dẫn giải:

\(A B\) // \(D E\).

Theo hệ quả của định lí Thalès ta có:

\(\frac{C A}{C E} = \frac{C B}{C D} = \frac{A B}{D E} = \frac{5}{15} = \frac{1}{3}\)

Hay:

\(\frac{C B}{C D} = \frac{1}{3}\) suy ra \(\frac{x}{7 , 2} = \frac{1}{3}\).

Vậy \(x = \frac{7 , 2. \&\text{nbsp}; 1}{3} = 2 , 4\)

 suy ra \(\frac{3}{y} = \frac{1}{3}\)

Vậy \(y = \frac{3.3}{1} = 9\).

Hướng dẫn giải:

\(\frac{2 x - 50}{50} + \frac{2 x - 51}{49} + \frac{2 x - 52}{48} + \frac{2 x - 53}{47} + \frac{2 x - 200}{25} = 0\)

\(\frac{2 x - 50}{50} + \frac{2 x - 51}{49} + \frac{2 x - 52}{48} + \frac{2 x - 53}{47} + \frac{2 x - 100}{25} + \frac{- 100}{25} = 0\)

\(\frac{2 x - 50}{50} + \frac{2 x - 51}{49} + \frac{2 x - 52}{48} + \frac{2 x - 53}{47} + \frac{2 x - 100}{25} + \left(\right. - 4 \left.\right) = 0\)

\(\frac{2 x - 50}{50} - 1 + \frac{2 x - 51}{49} - 1 + \frac{2 x - 52}{48} - 1 + \frac{2 x - 53}{47} - 1 + \frac{2 x - 100}{25} = 0\)

\(\frac{2 x - 100}{50} + \frac{2 x - 100}{49} + \frac{2 x - 100}{48} + \frac{2 x - 100}{47} + \frac{2 x - 100}{25} = 0\)

\(\left(\right. 2 x - 100 \left.\right) . \left(\right. \frac{1}{50} + \frac{1}{49} + \frac{1}{48} + \frac{1}{47} + \frac{1}{25} \left.\right) = 0\)

\(2 x - 100 = 0\) (Do \(\frac{1}{50} + \frac{1}{49} + \frac{1}{48} + \frac{1}{47} + \frac{1}{25} \neq 0\))

\(x = 50\).

Vậy phương trình đã cho có nghiệm \(x = 50\).

x+1​=52x+5​

\(\frac{5 \left(\right. x + 1 \left.\right)}{15} = \frac{3 \left(\right. 2 x + 5 \left.\right)}{15}\)

\(5 x + 5 = 6 x + 15\)

\(5 x - 6 x = 15 - 5\)

\(- x = 10\)

\(x = - 10\).

Vậy phương trình có tập nghiệm \(S = \left{\right. - 10 \left.\right}\).

a)  Với \(x \neq \&\text{nbsp}; \frac{1}{3}\), \(x \neq - \frac{1}{3}\). ta có:

\(P = \&\text{nbsp}; \left(\right. \frac{2 x}{3 x + 1} - 1 \left.\right) : \left(\right. 1 - \frac{8 x^{2}}{9 x^{2} - 1} \left.\right)\)

\(= \frac{2 x - 3 x - 1}{3 x + 1} : \frac{9 x^{2} - 1 - 8 x^{2}}{9 x^{2} - 1}\)

\(= \frac{- \left(\right. x + 1 \left.\right)}{3 x + 1} . \frac{9 x^{2} - 1}{x^{2} - 1}\)

\(= \frac{- \left(\right. x + 1 \left.\right)}{3 x + 1} . \frac{\left(\right. 3 x + 1 \left.\right) \left(\right. 3 x - 1 \left.\right)}{\left(\right. x + 1 \left.\right) \left(\right. x - 1 \left.\right)}\)

\(= \frac{1 - 3 x}{x - 1}\).

b) Thay \(x = 2\) vào biểu thức ta có:

     \(P = \frac{1 - 3.2}{2 - 1} = - 5\).

a) \(\frac{2 y - 1}{y} - \frac{2 x + 1}{x}\)

\(= \frac{x \left(\right. 2 y - 1 \left.\right)}{x y} - \frac{y \left(\right. 2 x + 1 \left.\right)}{x y}\)

\(= \frac{2 x y - x - 2 x y - y}{x y} = \frac{- x - y}{x y}\).

b) \(\frac{2 x}{3} : \frac{5}{6 x^{2}}\)

\(\frac{2 x}{3} : \frac{5}{6 x^{2}} = \frac{2 x}{3} . \frac{6 x^{2}}{5}\)

\(= \frac{4 x^{3}}{5}\).

Ta có: \(\frac{x - a}{b c} + \frac{x - b}{c a} + \frac{x - c}{a b} = \frac{2}{a} + \frac{2}{b} + \frac{2}{c}\)

\(\left(\right. \frac{x - a}{b c} - \frac{2}{a} \left.\right) + \left(\right. \frac{x - b}{c a} - \frac{2}{b} \left.\right) + \left(\right. \frac{x - c}{a b} - \frac{2}{c} \left.\right) = 0\)

\(\frac{a \left(\right. x - a \left.\right) - 2 b c + b \left(\right. x - b \left.\right) - 2 c a + c \left(\right. x - c \left.\right) - 2 a b}{a b c} = 0\)

Điều kiện xác định: \(a , b , c \neq 0\)

Khi đó: \(\frac{\left(\right. a + b + c \left.\right) x - a^{2} - 2 b c - b^{2} - 2 c a - c^{2} - 2 a b}{a b c} = 0\)

\(\left(\right. a + b + c \left.\right) x = \left(\left(\right. a + b + c \left.\right)\right)^{2}\) 

+ Nếu \(a + b + c = 0\) thì phương trình có vô số nghiệm.

+ Nếu \(a + b + c \neq 0\) thì phương trình có nghiệm duy nhất \(x = a + b + c\).

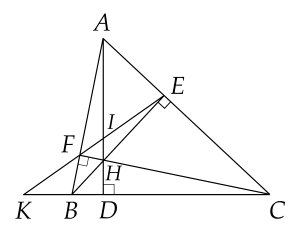
a) Xét \(\Delta A B E\) và \(\Delta A C F\) có:

\(\hat{B A C}\) chung;

\(\hat{A E B} = \hat{A F C} = 90^{\circ}\);

Do đó \(\Delta A B E \sim \Delta A C F\) (g.g).

Suy ra \(\frac{A B}{A C} = \frac{A E}{A F}\) nên \(A B . A F = A C . A E\).

b) Từ \(A B . A F = A C . A E\) suy ra \(\frac{A E}{A F} = \frac{A B}{A C}\).

Xét \(\Delta A E F\) và \(\Delta A B C\) có:

\(\frac{A E}{A F} = \frac{A B}{A C}\) (cmt);

\(\hat{B A C}\) chung;

Do đó \(\Delta A E F \sim \Delta A B C\) (c.g.c)

Suy ra \(\hat{A F E} = \hat{A C B}\) (cặp góc tương ứng).

c) Xét \(\Delta C E B\) và \(\Delta C D A\) có:

\(\hat{A C B}\) chung;

\(\hat{C E B} = \hat{C D A} = 90^{\circ}\)

Do đó \(\Delta C E B \sim \Delta C D A\) (g.g)

Suy ra \(\frac{C B}{C E} = \frac{C A}{C D}\) (cặp cạnh tương ứng).

Xét \(\Delta C B A\) và \(\Delta C E D\) có:

\(\frac{C B}{C E} = \frac{C A}{C D}\) (cmt);

\(\hat{A C B}\) chung;

Do đó \(\Delta C B A \sim \Delta C E D\) (c.g.c)

Suy ra \(\hat{C D E} = \hat{C A B}\) (cặp góc tương ứng) (1)

Tương tự: \(\hat{B D F} = \hat{C A B}\) (2).

Từ (1) và (2) suy ra \(\hat{C D E} = \hat{B D F}\).

Mà \(\hat{C D E} + \hat{E D A} = \hat{B D F} + \hat{F D A}\) suy ra \(\hat{E D A} = \hat{F D A}\).

Suy ra \(D A\) là phân giác của góc \(E D F\).

Mặt khác \(A D \bot K D\) nên \(D K\) là phân giác ngoài của \(\Delta D E F\).

Ta có \(D I\) là phân giác trong của \(\Delta \&\text{nbsp}; D E F\) suy ra \(\frac{I F}{I E} = \frac{D F}{D E}\) (3)

Ta có \(D K\) là phân giác ngoài của \(\Delta D E F\) suy ra \(\frac{K F}{K E} = \frac{D F}{D E}\) (4)

Từ (3) và (4) suy ra \(\frac{I F}{I E} = \frac{K F}{K E}\).

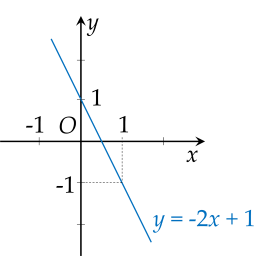
Với \(m = - 1\), hàm số trở thành \(y = - 2 x + 1\).

Xét hàm số \(y = - 2 x + 1\) :

Thay \(x = 0\) thì \(y = 1\).

Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 0 ; 1 \left.\right)\).

Thay \(x = 1\) thì \(y = - 1\).

Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 1 \left.\right)\).

Vẽ đồ thị:

b) Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) song song với đường thẳng \(\left(\right. d^{'} \&\text{nbsp}; \left.\right) : y = - 3 x + 9\) nên: \(a \neq - 3 ; b \neq 9\).

Khi đó ta có: \(\left(\right. d \left.\right) : y = - 3 x + b\) và \(b \neq 9\).

Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) đi qua \(A \left(\right. 1 ; - 8 \left.\right)\) nên: \(- 8 = - 3.1 + b\)

Suy ra \(b = - 5\) (thoả mãn)

Vậy đường thẳng cần tìm là \(\left(\right. d \left.\right) : y = - 3 x - 5\).

Bài 1:

a, 3x - 5 = 4

3x = 4 + 5

x = 3

vậy nghiệm của phương trình là x = 3

b,\(\frac{ x}{3} + \frac{3 x - 1}{6} = \frac{x}{2}\)

\(\frac{4 x}{6} + \frac{3 x - 1}{6} = \frac{3 x}{6}\)

\(4 x + 3 x - 1 = 3 x\)

\(4 x = 1\)

\(x = \frac{1}{4}\)

Vậy phương trình có nghiệm \(x = \frac{1}{4}\).

- Môi trường trên cạn: nấm linh chi, xương rồng, hươu cao cổ, chim bồ câu.

- Môi trường dưới nước: cá đuối, bạch tuộc.

- Môi trường trong đất: giun đất, dế trũi.

- Môi trường sinh vật: sâu đục thân, vi khuẩn E. coli.