

Dương Lê Thảo Vy
Giới thiệu về bản thân



































a: \(\mathit{A} \mathit{K} + \mathit{K} \mathit{C} = \mathit{A} \mathit{C}\)
=>\(\mathit{K} \mathit{C} = \mathit{A} \mathit{C} - \mathit{A} \mathit{K} = \mathit{A} \mathit{C} - \frac{1}{3} \mathit{A} \mathit{C} = \frac{2}{3} \mathit{A} \mathit{C} = 2 \cdot \frac{1}{3} \mathit{A} \mathit{C} = 2 \cdot \mathit{A} \mathit{K}\)
=>\(\mathit{S}_{\mathit{B} \mathit{K} \mathit{C}} = 2 \cdot \mathit{S}_{\mathit{A} \mathit{B} \mathit{K}}\)
b: Vì \(\frac{\mathit{A} \mathit{I}}{\mathit{A} \mathit{B}} = \frac{\mathit{A} \mathit{K}}{\mathit{A} \mathit{C}} \left(\right. = \frac{1}{3} \left.\right)\)
nên IK//BC
=>\(\frac{\mathit{O} \mathit{I}}{\mathit{O} \mathit{C}} = \frac{\mathit{I} \mathit{K}}{\mathit{B} \mathit{C}} = \frac{1}{3}\)
=>\(\frac{\mathit{I} \mathit{O}}{\mathit{I} \mathit{C}} = \frac{1}{3 + 1} = \frac{1}{4}\)
=>IO=32/4=8(cm)
c: Ta có: IO=1/4IC
=>IO=1/4*32=8(cm)
Ta có: IO+OC=IC
=>OC+8=32
=>OC=32-8=24(cm)
Lời giải:
Có ba góc, đó là 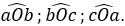
Viết bài luận thuyết phục người khác từ bỏ một thói quen: Trì hoãn công việc
Cuộc sống là một chuỗi những hành trình, để thực hiện những mục tiêu, dự định con người cần lên kế hoạch và thực hiện tốt những công việc. Thời gian để hiện thực hóa mục tiêu của mỗi người lại không giống nhau, có người thực hiện một cách nhanh chóng trong một khoảng thời gian xác định, cũng có người phải mất khoảng thời gian rất dài mới có thể thực hiện được. Có sự khác nhau này không chỉ do định hướng, cách thức thực hiện của con người mà còn bị chi phối bởi thói quen trì hoãn công việc.
“Công việc” là những mục tiêu, dự định trước mắt mà chúng ta cần thực hiện. “Trì hoãn” là kéo dài, làm gián đoạn tiến độ công việc. Thói quen trì hoãn công việc đang là một trong những thói quen chưa tốt của con người trong việc thực hiện những mục tiêu công việc.
Cuộc sống có rất nhiều biến động, trong đó có nhiều điều bất thường có thể xảy ra ngoài ý muốn của con người. Những thay đổi đó có thể làm gián đoạn buộc con người phải trì hoãn công việc đang thực hiện để giải quyết những vấn đề trước mắt. Chẳng hạn, công việc hàng ngày của người học sinh là học tập, nhưng vì những lí do bất ngờ: thời tiết, sức khỏe, phương tiện đi lại, người học có thể phải trì hoãn công việc học để giải quyết những vấn đề phát sinh trước mắt ấy.
Tuy nhiên, đó chỉ là việc trì hoãn tạm thời, còn thói quen trì hoãn công việc lại là thói quen được lặp đi lặp lại nhiều lần ở con người. Thói quen trì hoãn có thể mang đến nhiều hậu quả tiêu cực đối với cuộc sống, trước hết nó hình thành tâm lí ỷ lại, lười biếng, đứng trước một công việc cần phải giải quyết nhưng mãi ngần ngừ không chịu thực hiện và trì hoãn cho đến ngày hôm sau, ngày sau nữa hoặc một khoảng thời gian không xác định nào đó.
Trì hoãn công việc ảnh hưởng trực tiếp đến tiến độ và kết quả của công việc, trì hoãn khiến ta không hoàn thành nhiệm vụ đúng thời hạn, thậm chí thói quen trì hoãn khiến cho con người bỏ lỡ những cơ hội, những điều kiện tốt để phát triển và khẳng định giá trị của bản thân.
Thói quen trì hoãn công việc còn làm nảy sinh tính bê trễ, thiếu kỉ luật, trách nhiệm với bản thân cũng như với công việc được giao. Nếu duy trì thói quen xấu này, con người không chỉ khó khăn trong việc thực hiện những mục tiêu, bỏ lỡ cơ hội để phát triển, thăng tiến mà còn đánh mất đi uy tín, làm giảm đi giá trị của bản thân trong mắt đối tác cũng như mọi người xung quanh.
Trì hoãn làm cho con người trở nên lười biếng, không phát huy được sự cố gắng, nỗ lực, kĩ năng giải quyết, xử lí mọi việc cũng bị giảm sút đáng kể.
Trì hoãn công việc là thói quen không tốt cần được nhận thức và thay đổi nếu như muốn phát triển và hoàn thiện bản thân, đừng tạo điều kiện cho sự lười biếng và những suy nghĩ thiếu quyết đoán phát triển, đừng để thói quen trì hoãn trở thành vật cản đường trong hành trình đến với thành công các bạn nhé!
Viết bài luận thuyết phục người khác từ bỏ một quan niệm: nhuộm tóc là hư hỏng
Ngày nay, đi trên đường phố, ta bắt gặp rất nhiều người nhuộm tóc. Tôi cho rằng đó là một chuyện làm đẹp hết sức chính đáng và bình thường của con người. Tuy nhiên, vẫn có những quan điểm cho rằng, việc nhuộm tóc là hư hỏng. Đây là một quan niệm chưa có sự cởi mở nếu nói là sai lầm. Để lí giải cụ thể, tôi xin được trình bày trong bài viết này.
Các cụ ta vẫn có câu: “Cái răng, cái tóc là góc con người”. Thật vậy, nhìn vào hàm răng, mái tóc của một người có thể biết đó là người chăm chỉ, gọn gàng hay không. Nhìn vào hàm răng, mái tóc của một người, ta cũng có thể biết người đó có để ý đến vẻ bề ngoài của bản thân hay không. Vậy là, từ xa xưa, chuyện “tóc tai”, làm đẹp cũng đã được các cụ nhà ta để ý. Quan niệm cho rằng nhuộm tóc là hư hỏng một phần đến từ quan niệm về thẩm mỹ. Màu tóc của người Việt Nam vốn là màu đen. Đến khi cao tuổi, tóc từ màu đen sẽ đổi sang màu trắng. Quan niệm về cái tự nhiên, về cái quen mắt là đẹp vốn đã có hàng nghìn năm. Thời ấy, chưa có công nghệ hiện đại và sự phát triển như bây giờ. Thế nên, chắc chắn con người ta chỉ có thể để màu của tóc theo tự nhiên và dần hình thành quan niệm về cái đẹp của mái tóc. Ngày nay, con người ta vẫn giống như ngày trước, vẫn có nhu cầu làm đẹp, vẫn biết để ý đến hình thức của bản thân. Chỉ có điều, quan niệm về thẩm mỹ đã có sự đổi khác, mái tóc không nhất thiết phải là màu đen. Nói đến quan niệm thẩm mỹ, ta có thể chỉ ra một ví dụ, trước kia, ở nước ta có tục nhuộm răng đen. Nhưng thời đại ngày nay, chẳng còn mấy người nhuộm răng như vậy nữa.
Tôi cho rằng, việc nhuộm tóc chỉ cần phù hợp với điều kiện kinh tế, phù hợp với bản thân và không gây hấn với xã hội là được. Chúng ta sẽ khó thể nào mà chấp nhận một người khỏa thân đi ở ngoài đường. Điều đó vẫn nằm ngoài sức tưởng tượng và mức độ chịu đựng của tôi. Nhưng với mái tóc, tôi thấy không có vấn đề gì cả. Con người có quyền lựa chọn màu tóc là một cách để thể hiện cá tính, để làm đẹp và để tự tin hơn.
Nhuộm tóc chưa chắc đã là hư hỏng và không nhuộm tóc chưa chắc đã là không hư hỏng. Tôi đã được biết đến một tội phạm giết người ở Việt Nam vào khoảng năm 2011. Anh ta là một người có mái tóc màu đen. Tôi cũng được biết đến hoa hậu Nguyễn Thúc Thùy Tiên, một cô gái biết sử dụng tiếng Việt, tiếng Anh, tiếng Thái, tràn đầy tự tin và cống hiến, có mái tóc nhuộm màu nâu. Và chính bản thân tôi, một học sinh có thể coi là ưu tú, con ngoan trò giỏi trong lớp, cũng đã từng nhuộm tóc.
Tôi chỉ mong rằng chúng ta sẽ nhìn nhận một cách đúng đắn, bao dung, bớt khắt khe hơn về việc nhuộm tóc. Vì chỉ khi cố gắng tìm hiểu một điều gì đó, ta mới có cơ hội để hiểu được tận gốc của vấn đề.
Henry Brooks Adams từng nói: “Biết cách học là đủ chứng tỏ bạn thông thái”. Quả đúng là như vậy, phương pháp học tập đúng đắn sẽ tạo nên hiệu quả tích cực. Học tập là nhiệm vụ của học sinh. Để duy trì thành tích học tập tốt, bên cạnh việc chăm chú nghe giảng, học tập trên lớp, thời gian tự học thông qua làm bài tập về nhà cũng vô cùng quan trọng. Tuy nhiên, hiện nay phần lớn các học sinh có thói quen không làm bài tập ở nhà.
Vậy bạn có biết tại sao học sinh chúng ta ngày càng lười làm bài tập không? Với tôi, tôi cảm thấy bài tập về nhà rất khó và làm tốn rất nhiều thời gian, vì vậy tôi thường trì hoãn việc làm bài của mình. Vậy còn các bạn thì sao? Nhiều học sinh cho rằng học tập là một nhiệm vụ bắt buộc nên luôn thực hiện nó một cách đối phó. Cũng có nhiều học sinh cho rằng thời gian học tập trên lớp là đủ và không muốn phải tiếp tục học khi về nhà. Và cũng có những học sinh cảm thấy áp lực trong học tập, chán ghét và sợ hãi việc học. Đó là những lí do hình thành thói quen không làm bài tập về nhà ở phần lớn học sinh hiện nay. Sau mỗi buổi học trên lớp, giáo viên thường giao cho học sinh một số câu hỏi bài tập để củng cố thêm kiến thức. Tuy nhiên, chỉ cần bước chân ra khỏi lớp học, đôi khi chúng ta sẽ quên ngay mọi lời giáo viên nói. Và khi trở về nhà, chúng ta bị thu hút bởi những cuộc vui, bởi những trò chơi điện tử hay đơn giản là vì lười nên không muốn làm gì cả. Thói quen làm bài tập ở nhà của học sinh hiện nay chủ yếu là đối phó. Chúng ta thường tìm lời giải trên mạng rồi chép lại mang đến lớp nộp để giáo viên kiểm tra mà không hề tự cố gắng làm bài. Hoặc chăm hơn một chút, có những học sinh sẽ tự ngồi làm bài tập về nhà nhưng chỉ làm một cách qua loa, không đầu tư nhiều thời gian và công sức. Cũng có những bạn sẽ không làm ở nhà mà đến lớp, sát giờ học mở vở ra mới nhận ra có bài tập và vội vàng làm hoặc sẽ mượn bài của các bạn trong lớp chép. Và cũng sẽ có những bạn không quan tâm đến việc có bài tập, không làm và đến lớp học với một cái đầu trống rỗng. Có lẽ những biểu hiện trên đều đã từng xuất hiện trong chính chúng ta ít nhất một lần trong đời.
Không làm bài tập ở nhà là một thói quen xấu. Vậy nếu không thể từ bỏ thói quen ấy, điều gì sẽ xảy ra? Chắc hẳn chúng ta đều biết bất kì thói quen xấu nào cũng hình thành nên những tính cách xấu. Nếu không làm bài tập ở nhà dần trở thành một thói quen, chúng ta sẽ trở thành một con người lười biếng, ì trệ, luôn phụ thuộc vào người khác. Không chỉ trong học tập mà trong bất kì công việc nào của cuộc sống, thói quen trì hoãn sẽ khiến ta không bao giờ hoàn thành được điều mình mong muốn. Chủ tịch Hồ Chí Minh từng dạy: “Học với hành phải đi đôi. Học mà không hành thì vô ích. Hành mà không học thì hành không trôi chảy”. Câu nói ấy đến nay vẫn còn nguyên những giá trị. Học tập và tiếp nhận lí thuyết ở trên lớp thôi chưa đủ, quan trọng chúng ta cần phải biết vận dụng những kiến thức được học vào thực hành làm bài tập và áp dụng trong cuộc sống. Tự mình hoàn thành bài tập ở nhà chính là một cách giúp chúng ta rèn luyện thực hành. Nhờ đó, kiến thức tiếp thu được ở trên lớp sẽ được hiểu sâu và kĩ hơn. Ngược lại, nếu không làm bài tập ở nhà, kiến thức chúng ta tiếp thu sẽ nhanh chóng bị lãng quên, ảnh hưởng rất lớn đến kết quả học tập. Việc hằng ngày đến lớp mượn vở bạn bè để chép đôi khi còn gây phiền hà với bạn bè xung quanh, đánh mất niềm tin ở bạn bè. Hơn nữa, nếu tất cả các học sinh đều không cố gắng ôn luyện làm bài tập, giáo viên sẽ không thể có những bài học hiệu quả. Việc thiếu ý thức làm bài tập ở nhà của học sinh không chỉ khiến bố mẹ buồn phiền mà thầy cô, nhà trường cũng vô cùng lo lắng.
Không làm bài tập ở nhà đang dần trở thành một thói quen xấu có ở mọi học sinh. Vậy chúng ta cần làm gì để loại bỏ thói quen ấy? Chúng ta biết rằng để từ bỏ một thói quen không phải là công việc dễ dàng. Vì vậy, hãy bắt đầu rèn luyện từ những điều nhỏ nhất. Trước hết, bạn hãy thiết kế cho mình một thời gian biểu hợp lý. Đối với bài tập về nhà, bạn đừng để khi hôm sau có tiết thì hôm nay mới làm, hãy hoàn thành nó vào ngay buổi tối mà các bạn học môn đó. Bởi đó là lúc kiến thức của bạn đang được lưu trữ tốt nhất và việc làm bài tập sẽ khiến bạn nhớ bài lâu hơn, học tập hiệu quả hơn. Như vậy, khi đến tiết học sau, bạn có thể chủ động và tự tin đến lớp khi tất cả các bài tập đã được hoàn thành. Bạn hãy tự tạo cho mình một không gian học tập hiệu quả bằng cách tách biệt với các thiết bị di động, những thứ có thể làm mình bị sao nhãng, ảnh hưởng. Trong một buổi tối, bạn có thể dành ra 1-2 tiếng để tự học và đặt thời gian nghỉ giữa giờ khoảng 10-15 phút. Với những bài tập khó, bạn có thể nhắn tin nhờ thầy cô hướng dẫn hoặc trao đổi với bạn bè. Một cách học hiệu quả đó chính là chúng ta học nhóm cùng với bạn bè của mình. Như vậy bạn vừa có thể tiếp thu kiến thức từ bạn bè, vừa có thể tự rèn luyện bản thân, nhận ra được những nhược điểm của mình và tìm cách khắc phục. Thay vì để bố mẹ, thầy cô nhắc nhở làm bài tập, chúng ta nên chủ động và tự giác hoàn thành công việc của mình. Bởi học tập là nghĩa vụ của học sinh, chúng ta phải có trách nhiệm với cuộc sống của chính mình. Tuy nhiên, đừng nghĩ việc hoàn thành bài tập ở nhà như một trách nhiệm nặng nề, hãy nghĩ đó là quá trình bạn đang hoàn thiện mình. Kiến thức khi chúng ta tự học và chủ động tiếp nhận là những kiến thức được chúng ta lưu giữ lâu và hiệu quả nhất.
Có thể các bạn sẽ cho rằng thời gian học ở trên lớp là quá nhiều vậy còn học ở nhà làm gì? Hoặc các bạn sẽ cảm thấy việc học và làm bài tập liên tục như vậy sẽ giống như một con “mọt sách”. Cũng có những bạn cho rằng giáo viên giao quá nhiều bài tập khiến chúng ta cảm thấy áp lực và sợ hãi việc học. Những điều các bạn thắc mắc đều hợp lý với tâm lý của phần lớn học sinh hiện nay. Vậy bạn thử nghĩ mà xem, nếu một ngày giáo viên không giao cho các bạn những bài tập ôn luyện, nếu một ngày bạn đã lãng quên hoàn toàn việc tự học ở nhà và nếu một ngày, kiến thức của tất cả học sinh đều chỉ phụ thuộc vào những giờ phút học ít ỏi trên lớp, điều gì sẽ xảy ra? Kiến thức đến với con người nếu không được ôn tập và rèn luyện sẽ nhanh chóng tan biến. Như vậy, làm sao những học sinh có thể nắm vững tri thức để cống hiến cho cộng đồng? Làm sao nền giáo dục có thể phát triển? Làm sao con người và xã hội mới có thể trở nên văn minh? Việc không làm bài tập ở nhà có thể thấy chỉ là một thói quen rất nhỏ nhưng nếu không tìm cách từ bỏ, nó sẽ làm ảnh hưởng đến tính cách con người cũng như trình độ phát triển của xã hội. Tuy nhiên, cũng cần nhận thấy rằng hệ thống giáo dục cần đổi mới phương pháp giao bài tập để học sinh cảm thấy hứng thú hơn với việc học. Thay vì giao bài tập về nhà, giáo viên có thể giao nhiệm vụ chuẩn bị kiến thức cho buổi học sau. Như vậy, học sinh sẽ có được tâm thế chủ động hơn khi đến lớp. Thay vì giao những bài tập viết, giáo viên có thể giao học sinh những bài tập thực hành, làm việc theo nhóm để học sinh phát huy khả năng tư duy, sáng tạo. Như vậy, dù học tập theo hình thức nào, ý thức tự giác, chủ động của học sinh vẫn luôn là yếu tố vô cùng quan trọng.
Nếu có thể từ bỏ thói quen không làm bài tập ở nhà, chắc chắn bạn sẽ đạt được kết quả học tập mong muốn và theo đuổi được ước mơ của mình. Hãy rèn luyện cho bản thân sự tự giác, chủ động không chỉ trong học tập mà còn trong mọi mặt đời sống.
Henry Brooks Adams từng nói: “Biết cách học là đủ chứng tỏ bạn thông thái”. Quả đúng là như vậy, phương pháp học tập đúng đắn sẽ tạo nên hiệu quả tích cực. Học tập là nhiệm vụ của học sinh. Để duy trì thành tích học tập tốt, bên cạnh việc chăm chú nghe giảng, học tập trên lớp, thời gian tự học thông qua làm bài tập về nhà cũng vô cùng quan trọng. Tuy nhiên, hiện nay phần lớn các học sinh có thói quen không làm bài tập ở nhà.
Vậy bạn có biết tại sao học sinh chúng ta ngày càng lười làm bài tập không? Với tôi, tôi cảm thấy bài tập về nhà rất khó và làm tốn rất nhiều thời gian, vì vậy tôi thường trì hoãn việc làm bài của mình. Vậy còn các bạn thì sao? Nhiều học sinh cho rằng học tập là một nhiệm vụ bắt buộc nên luôn thực hiện nó một cách đối phó. Cũng có nhiều học sinh cho rằng thời gian học tập trên lớp là đủ và không muốn phải tiếp tục học khi về nhà. Và cũng có những học sinh cảm thấy áp lực trong học tập, chán ghét và sợ hãi việc học. Đó là những lí do hình thành thói quen không làm bài tập về nhà ở phần lớn học sinh hiện nay. Sau mỗi buổi học trên lớp, giáo viên thường giao cho học sinh một số câu hỏi bài tập để củng cố thêm kiến thức. Tuy nhiên, chỉ cần bước chân ra khỏi lớp học, đôi khi chúng ta sẽ quên ngay mọi lời giáo viên nói. Và khi trở về nhà, chúng ta bị thu hút bởi những cuộc vui, bởi những trò chơi điện tử hay đơn giản là vì lười nên không muốn làm gì cả. Thói quen làm bài tập ở nhà của học sinh hiện nay chủ yếu là đối phó. Chúng ta thường tìm lời giải trên mạng rồi chép lại mang đến lớp nộp để giáo viên kiểm tra mà không hề tự cố gắng làm bài. Hoặc chăm hơn một chút, có những học sinh sẽ tự ngồi làm bài tập về nhà nhưng chỉ làm một cách qua loa, không đầu tư nhiều thời gian và công sức. Cũng có những bạn sẽ không làm ở nhà mà đến lớp, sát giờ học mở vở ra mới nhận ra có bài tập và vội vàng làm hoặc sẽ mượn bài của các bạn trong lớp chép. Và cũng sẽ có những bạn không quan tâm đến việc có bài tập, không làm và đến lớp học với một cái đầu trống rỗng. Có lẽ những biểu hiện trên đều đã từng xuất hiện trong chính chúng ta ít nhất một lần trong đời.
Không làm bài tập ở nhà là một thói quen xấu. Vậy nếu không thể từ bỏ thói quen ấy, điều gì sẽ xảy ra? Chắc hẳn chúng ta đều biết bất kì thói quen xấu nào cũng hình thành nên những tính cách xấu. Nếu không làm bài tập ở nhà dần trở thành một thói quen, chúng ta sẽ trở thành một con người lười biếng, ì trệ, luôn phụ thuộc vào người khác. Không chỉ trong học tập mà trong bất kì công việc nào của cuộc sống, thói quen trì hoãn sẽ khiến ta không bao giờ hoàn thành được điều mình mong muốn. Chủ tịch Hồ Chí Minh từng dạy: “Học với hành phải đi đôi. Học mà không hành thì vô ích. Hành mà không học thì hành không trôi chảy”. Câu nói ấy đến nay vẫn còn nguyên những giá trị. Học tập và tiếp nhận lí thuyết ở trên lớp thôi chưa đủ, quan trọng chúng ta cần phải biết vận dụng những kiến thức được học vào thực hành làm bài tập và áp dụng trong cuộc sống. Tự mình hoàn thành bài tập ở nhà chính là một cách giúp chúng ta rèn luyện thực hành. Nhờ đó, kiến thức tiếp thu được ở trên lớp sẽ được hiểu sâu và kĩ hơn. Ngược lại, nếu không làm bài tập ở nhà, kiến thức chúng ta tiếp thu sẽ nhanh chóng bị lãng quên, ảnh hưởng rất lớn đến kết quả học tập. Việc hằng ngày đến lớp mượn vở bạn bè để chép đôi khi còn gây phiền hà với bạn bè xung quanh, đánh mất niềm tin ở bạn bè. Hơn nữa, nếu tất cả các học sinh đều không cố gắng ôn luyện làm bài tập, giáo viên sẽ không thể có những bài học hiệu quả. Việc thiếu ý thức làm bài tập ở nhà của học sinh không chỉ khiến bố mẹ buồn phiền mà thầy cô, nhà trường cũng vô cùng lo lắng.
Không làm bài tập ở nhà đang dần trở thành một thói quen xấu có ở mọi học sinh. Vậy chúng ta cần làm gì để loại bỏ thói quen ấy? Chúng ta biết rằng để từ bỏ một thói quen không phải là công việc dễ dàng. Vì vậy, hãy bắt đầu rèn luyện từ những điều nhỏ nhất. Trước hết, bạn hãy thiết kế cho mình một thời gian biểu hợp lý. Đối với bài tập về nhà, bạn đừng để khi hôm sau có tiết thì hôm nay mới làm, hãy hoàn thành nó vào ngay buổi tối mà các bạn học môn đó. Bởi đó là lúc kiến thức của bạn đang được lưu trữ tốt nhất và việc làm bài tập sẽ khiến bạn nhớ bài lâu hơn, học tập hiệu quả hơn. Như vậy, khi đến tiết học sau, bạn có thể chủ động và tự tin đến lớp khi tất cả các bài tập đã được hoàn thành. Bạn hãy tự tạo cho mình một không gian học tập hiệu quả bằng cách tách biệt với các thiết bị di động, những thứ có thể làm mình bị sao nhãng, ảnh hưởng. Trong một buổi tối, bạn có thể dành ra 1-2 tiếng để tự học và đặt thời gian nghỉ giữa giờ khoảng 10-15 phút. Với những bài tập khó, bạn có thể nhắn tin nhờ thầy cô hướng dẫn hoặc trao đổi với bạn bè. Một cách học hiệu quả đó chính là chúng ta học nhóm cùng với bạn bè của mình. Như vậy bạn vừa có thể tiếp thu kiến thức từ bạn bè, vừa có thể tự rèn luyện bản thân, nhận ra được những nhược điểm của mình và tìm cách khắc phục. Thay vì để bố mẹ, thầy cô nhắc nhở làm bài tập, chúng ta nên chủ động và tự giác hoàn thành công việc của mình. Bởi học tập là nghĩa vụ của học sinh, chúng ta phải có trách nhiệm với cuộc sống của chính mình. Tuy nhiên, đừng nghĩ việc hoàn thành bài tập ở nhà như một trách nhiệm nặng nề, hãy nghĩ đó là quá trình bạn đang hoàn thiện mình. Kiến thức khi chúng ta tự học và chủ động tiếp nhận là những kiến thức được chúng ta lưu giữ lâu và hiệu quả nhất.
Có thể các bạn sẽ cho rằng thời gian học ở trên lớp là quá nhiều vậy còn học ở nhà làm gì? Hoặc các bạn sẽ cảm thấy việc học và làm bài tập liên tục như vậy sẽ giống như một con “mọt sách”. Cũng có những bạn cho rằng giáo viên giao quá nhiều bài tập khiến chúng ta cảm thấy áp lực và sợ hãi việc học. Những điều các bạn thắc mắc đều hợp lý với tâm lý của phần lớn học sinh hiện nay. Vậy bạn thử nghĩ mà xem, nếu một ngày giáo viên không giao cho các bạn những bài tập ôn luyện, nếu một ngày bạn đã lãng quên hoàn toàn việc tự học ở nhà và nếu một ngày, kiến thức của tất cả học sinh đều chỉ phụ thuộc vào những giờ phút học ít ỏi trên lớp, điều gì sẽ xảy ra? Kiến thức đến với con người nếu không được ôn tập và rèn luyện sẽ nhanh chóng tan biến. Như vậy, làm sao những học sinh có thể nắm vững tri thức để cống hiến cho cộng đồng? Làm sao nền giáo dục có thể phát triển? Làm sao con người và xã hội mới có thể trở nên văn minh? Việc không làm bài tập ở nhà có thể thấy chỉ là một thói quen rất nhỏ nhưng nếu không tìm cách từ bỏ, nó sẽ làm ảnh hưởng đến tính cách con người cũng như trình độ phát triển của xã hội. Tuy nhiên, cũng cần nhận thấy rằng hệ thống giáo dục cần đổi mới phương pháp giao bài tập để học sinh cảm thấy hứng thú hơn với việc học. Thay vì giao bài tập về nhà, giáo viên có thể giao nhiệm vụ chuẩn bị kiến thức cho buổi học sau. Như vậy, học sinh sẽ có được tâm thế chủ động hơn khi đến lớp. Thay vì giao những bài tập viết, giáo viên có thể giao học sinh những bài tập thực hành, làm việc theo nhóm để học sinh phát huy khả năng tư duy, sáng tạo. Như vậy, dù học tập theo hình thức nào, ý thức tự giác, chủ động của học sinh vẫn luôn là yếu tố vô cùng quan trọng.
Nếu có thể từ bỏ thói quen không làm bài tập ở nhà, chắc chắn bạn sẽ đạt được kết quả học tập mong muốn và theo đuổi được ước mơ của mình. Hãy rèn luyện cho bản thân sự tự giác, chủ động không chỉ trong học tập mà còn trong mọi mặt đời sống.
Dàn ý Viết bài luận thuyết phục người khác từ bỏ một thói quen hay một quan niệm
1. Mở bài: giới thiệu ngắn gọn vấn đề: cần từ bỏ quan niệm kỳ thị .
2. Thân bài.
a) Giải thích quan niệm:
b) Nguyên nhân của việc kỳ thị và phân biệt đối xử :
c) Hậu quả của việc kỳ thị và phân biệt đối xử đối
3. Kết bài: khẳng định lại vấn đề.
Viết bài luận thuyết phục người khác từ bỏ một thói quen: không làm bài tập về nhà
Từ lâu, làm bài tập về nhà đã trở thành nhiệm vụ quan trọng của người học sinh. Tuy nhiên, không phải cá nhân nào cũng nhận thức được điều đó. Một vài người đã hình thành và cho mình thói quen không làm bài tập về nhà. Đây là một thói quen xấu, cần gạt bỏ kịp thời.
Thông thường, sau mỗi tiết học, giáo viên bộ môn sẽ giao bài tập để học sinh củng cố và ôn tập kiến thức. Ấy vậy, vài bạn vẫn chưa nhận ra ý nghĩa thiết thực của thói quen này. Có bạn thì lười biếng, không muốn làm. Số khác lại bị hấp dẫn bởi điện thoại, mạng xã hội nên quên mất việc làm bài. Những bạn này thường dành thời gian cho các hoạt động vô bổ, không cần thiết như lướt Tiktok, Facebook, xem phim,... Một vài cá nhân luôn mang trong mình suy nghĩ ỷ lại vào người khác, đợi mai tới lớp chép bài bạn. Có thể nói, những nguyên nhân trên đây xuất phát từ chính bản thân mỗi học sinh.
Nếu thói quen này vẫn tiếp diễn, học sinh sẽ phải đối mặt với nhiều hậu quả khó lường. Trước hết, không làm bài tập về nhà đồng nghĩa với không tích lũy, bồi dưỡng các kiến thức quan trọng, dẫn đến tình trạng "học trước quên sau". Như vậy, đến kỳ thi hoặc kì kiểm tra, trong đầu chúng ta chẳng có tri thức. Từ đây, một số bạn sẽ bất chấp nội quy mà làm ra các hành vi tiêu cực như quay cóp, gian lận. Dần dần, kết quả học tập giảm sút, không có sự tiến bộ hoặc vươn lên tích cực.
Bạn thân mến, thực hiện một công việc mang ý nghĩa tốt đẹp thì chẳng bao giờ là vô bổ và tốn thời gian cả. Người xưa đã từng nói "học đi đôi với hành". Chỉ học lí thuyết mà không thực hành, vận dụng thì rất dễ quên. Hoàn thiện bài tập về nhà sẽ giúp chúng ta ôn tập các tri thức, đồng thời mở rộng, nâng cao bài học. Nhờ đó, chúng ta trở nên tự tin, hứng thú hơn trong việc học và kết quả cũng có sự cải thiện rõ rệt. Ngoài ra, làm bài tập về nhà cũng rèn luyện tinh thần tự giác, chăm chỉ, có trách nhiệm ở mỗi người.
Mỗi người phải nhận ra tầm quan trọng của việc học, dù là học trên trường lớp hay ở nhà. Hãy từ bỏ thói quen không làm bài tập về nhà ngay từ bây giờ, bạn nhé! Không ai cấm hay ngăn cản việc giải trí sau giờ học mệt mỏi nhưng mọi người cần tự cân bằng thời gian học và chơi. Chúng ta có thể lập thời gian biểu sao cho hợp lí, dành thời gian tự học khoảng 1-2 tiếng/ngày. Chúng ta cũng nên đề ra các mục tiêu cụ thể, nhằm kích thích tinh thần nỗ lực của bản thân. Khi gặp các vấn đề khó, chúng ta hãy cố gắng trao đổi với bạn bè, thầy cô thay vì chán nản, từ bỏ. Các bạn nên nhớ rằng không ai sinh ra đã là thiên tài, chỉ có "luyện mãi thành tài" mà thôi.
Bài tập về nhà chưa bao giờ là thừa thãi và vô tác dụng. Chúng ta hãy rèn luyện và bồi dưỡng thói quen thói quen tốt đẹp này để thêm chủ động, tự giác trong quá trình học. Từ đó, việc tích lũy tri thức của chúng ta sẽ hiệu quả hơn, tiến bộ hơn từng ngày.
Lần gần nhất mà bạn phải ngồi chờ đợi một ai đó là từ khi nào? Có lẽ thói quen đi trễ đã không còn xa lạ gì với mọi người nữa, nó gần như trở thành thói quen của rất nhiều người trong xã hội, đủ mọi tầng lớp, lứa tuổi,…và đặc biệt là ở lứa tuổi học sinh có thói quen đi học muộn với đủ mọi lí do hết sức vô lí được đưa ra.
Quản lý thời gian là một giải pháp cần thiết để khắc phục được tình trạng trễ giờ, quên thời gian,... và cần phải bố trí đủ thời gian vào buổi sáng để sẵn sàng đi học, trì hoãn các công việc không cần thiết cũng như dự đoán được các vấn đề về giao thông. Rất nhiều người không có ý thức sắp xếp, phân bổ thời gian một cách hợp lý, làm việc gì cũng chậm chạp và họ coi việc đi học muộn trở thành một việc hết sức bình thường. Việc đi đúng giờ không chỉ thể hiện bạn là một người văn minh, hiện đại mà còn là một người biết tôn trọng người khác. Chẳng hạn việc bạn thường xuyên đi trễ sẽ làm mất đi uy tín của bạn, lời hứa không còn có trọng lượng và bị đánh giá là người không đáng tin cậy. Nếu bạn nghĩ rằng đi học muộn là việc của bạn và hậu quả ra sao mình bạn chịu thì nhầm rồi nhé. Khi bạn đến lớp muộn, nó không chỉ làm gián đoạn dòng chảy của một bài giảng hoặc thảo luận, mà còn ảnh hưởng đến sự tập trung của học sinh khác, cản trở việc học của tập thể và thường ăn mòn tinh thần lớp học. Thầy cô cũng vì thế mà cảm thấy bực mình và không muốn dạy một lớp học mà có nhiều bạn vô ý thức, vô kỉ luật như vậy.
Việc mọi người đi trễ có thể do một sự cố ngẫu nhiên như: ngủ quên, tắc đường, nhỡ xe, thời tiết,…. nhưng cũng có thể đó đã trở thành một thói quen khó có cách nào sửa đổi. Có rất nhiều nguyên nhân khiến các bạn đến lớp muộn, có thể là nguyên nhân chủ quan với lí do làm bài tập ngủ muộn, sáng dậy muộn,… hay nguyên nhân khách quan như việc tắc đường, xe hỏng,…. Nhưng dù có là lý do gì đi nữa thì việc đi trễ vẫn là một thói quen không tốt để lại rất nhiều hậu quả đáng tiếc và chúng ta cần từ bỏ nó ngay từ bây giờ. Tác hại của việc đi trễ là vô cùng lớn. Nếu mỗi người trong xã hội đều không coi trọng việc đúng giờ thì xã hội sẽ không thể nào tiến bộ được. Để tránh tình trạng đi học muộn, các bạn hãy tự chọn cho mình một biện pháp khắc phục phù hợp với bản thân mình, giảm thiểu tối đa thời gian bị mất bởi những lí do không cần thĐi trễ không chỉ đơn thuần là một thói quen xấu mà còn là căn bệnh bám rễ vào tư tưởng mỗi người và có thể gây nên những hậu quả khó lường nếu không được khắc phục ngay từ bây giờ. Để khắc phục thói quen đi trễ của bản thân, đầu tiên bạn phải là một người biết coi trọng thời gian và đơn giản là có ý thức tôn trọng người khác và tôn trọng chính bản thân mình. Thứ nhất, bạn phải biết cách lập kế hoạch phân bổ thời gian trong ngày một cách hợp lí. Nếu bạn là người chậm chạp, lề mề trong việc chuẩn bị trước khi ra khỏi nhà thì hãy nhớ cài đồng hồ hẹn trước một chút thời gian để không bị lỡ hẹn và đi học đúng giờ. Thứ hai, nếu bạn là người đãng trí hay quên thì hãy tự lập cho mình một thời gian biểu khoa học và nhớ thường xuyên theo dõi nó để chắc chắn rằng mình không bỏ quên hay đi trễ một cuộc hẹn hay một buổi học nào cả. Và bạn cũng nên dự trù thời gian để có thể hoàn thành công việc và những việc có khả năng phát sinh thêm, tránh để quỹ thời gian của bạn bị quá tải, trôi đi một cách lãng phí.
Cha ông ta có câu: “Giang sơn dễ đổi, bản tính khó dời”. Dù biết rằng việc thay đổi thói quen từ thường xuyên đi trễ thành một người luôn đúng giờ là một việc làm rất khó nhưng không phải là không làm được. Vì vậy bạn và tôi, chúng ta đừng để đi muộn trở thành thói quen không thể sửa mà hãy cùng nhau trở thành người có thói quen làm việc khoa học và hiệu quả hơn. Hãy biết quý trọng thời gian!
iết.
Gợi ý thuyết phục từ bỏ thói quen vứt rác bừa bãi
Bước 1: Chuẩn bị viết
- Xác định đề tài: chọn một thói quen cần từ bỏ: Xả rác, chất thải không đúng nơi quy định.
- Xác định mục đích viết, đối tượng người đọc
+ Mục đích viết: thuyết phục người khác từ bỏ một thói quen có hại
+ Người đọc bài viết của bạn có thể là thầy cô giáo bộ môn, bạn bè cùng lớp, phụ huynh,...
- Thu thập tư liệu: Có thể thu thập từ truyền thông và từ những quan sát, trải nghiệm đời sống của chính bạn; nên ưu tiên thu thập tư liệu liên quan đến tác hại hay mặt trái của thói quen hoặc quan niệm mà mình muốn bác bỏ.
Bước 2: Tìm ý và lập dàn ý
Tìm ý
- Xác định hướng nghị luận về vấn đề: chẳng hạn bạn sẽ tập trung khẳng định hay bác bỏ hay kết hợp khẳng định với bác bỏ khi nghị luận về vấn đề.
- Ghi lại bất cứ ý tưởng nào nảy sinh trong đầu trong quá trình thu thập tài liệu và tìm ý cho bài viết.
- Phác hoạ một số luận điểm chính, rồi tìm lí lẽ, bằng chứng cho các luận điểm ấy.
Lập dàn ý: Bạn sắp xếp nội dung các phần mở bài, thân bài, kết bài; các luận điểm, lí lẽ và bằng chứng trong thân bài.
Dàn ý thuyết phục người khác từ bỏ thói quen vứt rác bừa bãi
1. Mở bài
Giới thiệu vấn đề cần thuyết phục: Hiện tượng vứt rác thải ra nơi công cộng.
2. Thân bài
a. Thực trạng
Ở những nơi công cộng: bệnh viện, nhà trường, các danh lam thắng cảnh không khó để bắt gặp những rác thải được vứt ngổn ngang bao gồm các loại rác thải từ mềm đến cứng bốc mùi hôi thối và gây ảnh hưởng đến cảnh quan của nơi công cộng đó.
b. Nguyên nhân
Chủ quan: do ý thức của người dân chưa tốt, tiện tay là vứt rác vì nghĩ nơi công cộng không phải là trách nhiệm của bản thân mình.
Khách quan: do lượng thùng rác ở nơi công cộng Việt Nam chưa đủ để đáp ứng được nhu cầu xả rác vô cùng lớn của người dân khiến cho rác thải vứt bừa bãi.
c. Hậu quả
- Lượng rác thải xả ra nhiều gây ảnh hưởng đến môi trường khi ngày nay ô nhiễm môi trường ngày càng tăng.
- Gây ảnh hưởng đến sức khỏe của con người; gây mất mĩ quan.
- Việc rác thải xả bừa bãi ở nơi công cộng gây khó khăn cho nhân viên vệ sinh trong việc thu gom và xử lí.
d. Giải pháp
- Mỗi con người cần tự giác ý thức phân loại rác thải, bỏ rác vào đúng nơi quy định ở những nơi công cộng.
- Mỗi nơi công cộng cần có những biển báo đổ rác thải, bố trí thùng rác hợp lí cũng như có những hình phạt thích đáng với những trường hợp xả rác bừa bãi.
- Nhà nước, các cấp quản lí cần tuyên truyền mạnh mẽ hơn nữa những tác hại của rác thải đồng thời có hình thức xử lí nghiêm khắc đối với những trường hợp vi phạm.
3. Kết bài
Khái quát lại vấn đề thuyết phục: hiện tượng vứt rác thải bừa bãi ra nơi công cộng đồng thời rút ra bài học, liên hệ bản thân.
Trong xã hội hiện đại ngày nay thì môi trường trở thành đối tượng được nhân loại quan tâm bảo vệ hàng đầu. Ở hầu hết những nước phát triển hiện tượng xả rác bừa bãi hầu như không còn tồn tại do người dân có ý thức cao trong bảo vệ môi trường. Tuy nhiên, bên cạnh bộ phận những người có ý thức ấy vẫn còn những người xả rác bừa bãi phá hoại môi trường sống của chúng ta.
Qúa trình sinh hoạt và sản xuất của con người tạo ra vô vàn các loại rác thải. Và nếu như không có một quy trình kiểm soát và xử lý kịp thời những loại rác thải đó thì sẽ gây ra những tác hại cho môi trường sống. Thế nhưng việc kiểm soát rác thải được thực hiện như thế nào là một vấn đề khó khăn. Thực tế chúng ta thấy rằng ý thức giữ gìn vệ sinh chung của một số người là chưa được tốt. Nhà cửa của mỗi người đều được quét dọn sạch sẽ, chẳng một ai vứt rác bừa bãi trong căn nhà của mình thế nhưng lại xả rác ngoài đường một cách vô ý thức. Hiện tượng này phổ biến ở mọi nơi, từ những thành phố lớn cho đến các miền quê. Có lẽ vì thế mà trên những đoạn đường vắng chúng ta sẽ thấy những túi rác, bao rác ngổn ngang ven đường, trên vỉa hè gây khó khăn cho người đi lại.
Trong những năm gần đây, các phương tiện thông tin đại chúng liên tục đưa tin về nạn ô nhiễm và cảnh báo hiện tượng trái đất đang bị huỷ hoại dần. Là một phần của sự sống chúng ta hãy cùng nhau giữ gìn môi trường xanh - sạch - đẹp. Hãy tích cực tham gia các hoạt động vì môi trường, tuyên truyền sâu rộng trong nhân dân để mọi người có thể hiểu được vai trò to lớn của môi trường sống. Việc tích cực giữ gìn sự trong lành của môi trường tự nhiên sẽ giúp cuộc sống của chúng ta ngày càng sạch đẹp, văn minh và tiến bộ.
Qua đây chúng ta thấy rằng môi trường thực sự quan trọng với chúng ta, vì vậy chúng ta không nên xả rác bừa bãi. Mỗi người chúng ta hãy góp phần làm trái đất sạch đẹp từ những hành động nhỏ nhất như không xả rác bừa bãi. Giữ gìn vệ sinh chung nơi công cộng và bỏ rác đúng nơi quy định thể hiện sự văn minh, lịch sự ở mỗi người chúng ta.
Thuốc kháng sinh là vũ khí tuyệt vời do con người tạo ra để chống lại các bệnh do nhiễm vi khuẩn, nhưng giờ đây vi khuẩn lại có khả năng đề kháng lại thuốc kháng sinh vốn được dùng để tiêu diệt chúng. Kháng kháng sinh đang là mối đe dọa lớn nhất đối với toàn ngành y tế nói riêng và cả xã hội nói chung.
Kháng sinh là thuốc tiêu diệt hoặc kiềm hãm sự phát triển của vi khuẩn, từ đó giảm đáp ứng viêm gây ra bởi vi khuẩn. Kháng sinh có tác dụng khác nhau trên từng loại vi khuẩn, một số kháng sinh có tác dụng trên nhiều chủng vi khuẩn được gọi là kháng sinh phổ rộng, một số loại khác tác dụng trên một số chủng vi khuẩn nhất định được gọi là phổ hẹp.
Hiện tượng kháng kháng sinh xảy ra khi mầm bệnh hay vi khuẩn có khả năng tạo ra cách chống lại thuốc kháng sinh làm cho kháng sinh không thể tiêu diệt hoặc ngăn chặn được sự phát triển của chúng.
Kháng kháng sinh đang là mối đe dọa lớn nhất đối với toàn ngành y tế nói riêng và cả xã hội nói chung khi bị ở bất cứ triệu chứng sức khỏe nào người dân cũng tự ý mua và sử dụng thuốc kháng sinh. Ngày nay do việc mua và sử dụng kháng sinh quá dễ dàng nên chỉ cần xuất hiện vài biểu hiện bất thường về sức khỏe như sốt, ho, sổ mũi là mọi người tự ý đến hiệu thuốc để mua kháng sinh, hay các bậc cha mẹ tự ý mua kháng sinh cho con mình sử dụng mà không cần biết con mình có nhiễm khuẩn hay không, trẻ em thì có phải uống liều như người lớn không và uống trong thời gian bao lâu là hợp lý.
Bên cạnh đó, các hiệu thuốc dễ dàng tự ý bán thuốc kháng sinh cho bệnh nhân mà không quan tâm bệnh nhân có toa của bác sĩ hay không, hay thậm chí bệnh nhân chỉ cần mang toa thuốc cũ, toa thuốc của người quen, hoặc chỉ cần bảo muốn mua thuốc kháng sinh là được.
Có nhiều loại bệnh lý khác nhau như bệnh miễn dịch, ngộ độc, bệnh chuyển hóa, bệnh nhiễm trùng v.v… Trong đó chỉ có bệnh nhiễm trùng là cần phải sử dụng kháng sinh. Trong các bệnh lý khác, sử dụng kháng sinh không những không giúp điều trị bệnh mà còn làm tăng tỷ lệ vi khuẩn kháng thuốc. Trong hầu hết các trường hợp sốt, đau họng, sổ mũi đa số là do virus gây nên, và kháng sinh thì chỉ có hiệu quả trên vi khuẩn. Theo Cục Quản lý khám chữa bệnh (Bộ Y tế), kết quả khảo sát việc bán thuốc kháng sinh ở các hiệu thuốc vùng nông thôn và thành thị cho thấy, nhận thức về kháng sinh và kháng thuốc của người bán thuốc lẫn người dân đều rất thấp. Có đến 88% số dân ở thành thị, 91% số dân ở nông thôn sử dụng kháng sinh không có đơn của bác sĩ”,....
Lạm dụng thuốc kháng sinh không chỉ lãng phí mà còn gây tổn hại đến sức khỏe, các bệnh do virut không chữa được bằng kháng sinh mà vẫn dùng kháng sinh. Gây khó khăn cho chẩn đoán: bệnh nhân bị viêm ruột thừa cấp mà dùng kháng sinh sẽ làm cho lu mờ các triệu chứng gây khó chẩn đoán. Có khi có tác dụng chữa nhưng lại dễ gây ra phản ứng dị ứng, mẫn cảm thậm chí nguy hiểm đến tính mạng. Sử dụng nhiều kháng sinh và liều cao có khả năng gây suy tủy, nhất là trường hợp sử dụng chloramphenicol nhiều. Một số kháng sinh như streptomycine, kanamycine dùng liều cao có thể gây điếc và suy thận. Lạm dụng kháng sinh làm cho vi khuẩn nhờn thuốc, kháng thuốc ngày càng nhiều, từ đó việc chữa trị bệnh càng khó khăn. Ngày nay các tụ cầu trùng kháng thuốc cephalosporin càng nhiều. Một số vi khuẩn khác cũng kháng thuốc do đó tác dụng chữa trị của kháng sinh ngày càng hạn chế. Nhiều người khi dùng thuốc kháng sinh chỉ cho rằng nó thuận tiện, giá thành cũng không quá đắt nhưng người dân lại đâu biết rằng tác hại của nó vô cùng nghiêm trọng. Vậy nên mọi người cần làm gì để hạn chế hay bỏ tình trạng lạm dụng thuốc kháng sinh? Nguyên tắc bạn cần biết khi dùng thuốc kháng sinh đó là chỉ điều trị bệnh do vi khuẩn gây ra và dùng chúng khi thực sự cần thiết, được bác sĩ đồng ý. Đúng liều: khi được bác sĩ kê đơn có thuốc kháng sinh, luôn uống đủ liều lượng đã được kê, không bỏ dở nửa chừng, ngay cả khi cảm thấy bệnh đã đỡ nhiều. Đúng chỉ dẫn: Không dùng thuốc kháng sinh thừa từ lần sử dụng trước; không chia sẻ thuốc kháng sinh trong toa thuốc đang dùng cho người khác uống, ngay cả khi đó là người thân của mình. Vì khi chia sẻ, sẽ thiếu liều thuốc cần uống và vô tình tạo cơ hội cho vi khuẩn mạnh mẽ lên và kháng lại các thuốc điều trị. Điều này gây nguy hiểm cho chính bản thân, cho gia đình và cộng đồng.
Nâng cao nhận thức ngay từ mỗi cá nhân bằng cách bắt đầu bằng thói quen tuân thủ đơn thuốc của bác sĩ, không tự ý mua kháng sinh về dùng cho bất cứ ai hoặc dùng trong chăn nuôi. Nhắc nhở những người quen nếu thấy họ dùng kháng sinh bừa bãi.
Có thể nói thói quen lạm dụng thuốc kháng sinh là một vấn đề cực kỳ nghiêm trọng mà chúng ta không nên chủ quan. Tốt nhất, mỗi người cần có ý thức sử dụng thuốc phù hợp, theo chỉ định của bác sĩ. Nếu sau một thời gian điều trị bạn không thấy hiệu quả, hãy đi tái khám và nhận tư vấn từ bác sĩ “hãy dùng kháng sinh đúng cách vì tương lai của chính chúng ta”.
Dàn ý Viết bài văn nghị luận thuyết phục mọi người từ bỏ thói quen lạm dụng thuốc kháng sinh
Mở bài
- Dẫn dắt và nêu vấn đề của bài viết:
Mọi người cần từ bỏ việc lạm dụng thuốc kháng sinh bởi thói quen này dẫn đến nhiều nguy cơ mà con người phải đối mặt trong điều trị bệnh tật.
Thân bài
- Sắp xếp các ý theo trật tự khác nhau, kết hợp giữa lí lẽ và dẫn chứng để thuyết phục mọi người từ bỏ thói quen lạm dụng thuốc kháng sinh:
+ Giải thích thế nào là thuốc kháng sinh, lạm dụng thuốc kháng sinh và trình bày hiện trạng lạm dụng thuốc kháng sinh hiện nay trong cộng đồng.
+ Những lí do để mọi người nên từ bỏ thói quen lạm dụng thuốc kháng sinh:
• Lạm dụng thuốc kháng sinh gây lãng phí tiền bạc.
• Lạm dụng thuốc kháng sinh gây khó khăn cho việc chẩn đoán, điều trị bệnh.
• Lạm dụng thuốc kháng sinh dẫn đến tình trạng kháng thuốc kháng sinh, gây nguy hiểm cho tính mạng.
+ Dự đoán lập luận của những người có thói quen lạm dụng thuốc kháng sinh (Ví dụ: dựa vào hướng dẫn của người bán thuốc; tham khảo thông tin trên mạng, không có thời gian để đi khám bác sĩ,...). Từ đó, người viết có thể phản biện lại. Chẳng hạn: Người bán thuốc không phải là bác sĩ khám bệnh, họ không đủ kiến thức chẩn đoán và kê đơn điều trị cho người bệnh.
+ Làm thế nào để từ bỏ thói quen lạm dụng thuốc kháng sinh (Ví dụ: hiểu tác hại của việc lạm dụng thuốc kháng sinh, khi có bệnh cần đi khám bác sĩ, mua và sử dụng thuốc theo đúng chỉ định của bác sĩ,...)?
Kết bài
Khẳng định lại thông điệp mọi người cần từ bỏ thói quen lạm dụng thuốc kháng sinh vì một cuộc sống khoẻ mạnh, an toàn cho bản thân và cộng
Dàn ý Bài luận thuyết phục người khác từ bỏ thói quen trì hoãn
a. Mở bài:
+ Giới thiệu: “Việc hôm nay chớ để ngày mai” là câu nói ai trong chúng ta cũng đã từng nghe và bắt gặp ít nhất một lần. Nội dung chính là nhắc nhở mỗi người thực hiện công việc một cách nghiêm túc, tránh trì hoãn.
+ Nêu vấn đề: “Thói quen trì hoãn” rất cần được được chúng ta cùng xem xét, bàn luận.
b. Thân bài:
- Khái niệm trì hoãn trong mọi việc là gì?
+ Trì hoãn: kéo dài, làm gián đoạn tiến độ. Trì hoãn công việc là chần chừ, chậm trễ trong giải quyết công việc dẫn đến mất rất nhiều thời gian để có thể hoàn thành mục tiêu đặt ra ban đầu.
+ Đây là một trong những thói quen không tốt.
- Biểu hiện của thói quen trì hoãn:
+ Trì hoãn công việc có thể bắt đầu từ những việc rất nhỏ, từ đôi ba phút lần lữa hay từ suy nghĩ “để mai làm cũng được”. Trên thực tế, rất ít người có thể nhận ra những mình đang trì hoãn công việc. Theo đó, bạn sẽ là người có thói quen trì hoãn công việc khi có một trong những biểu hiện dưới đây:
+ Không thực hiện công việc đã đặt ra theo lộ trình ban đầu.
+ Sẵn sàng gác lại công việc bởi những thứ không liên quan như phim ảnh, game,…
+ Có khả năng, điều kiện thực hiện công việc ngay lập tức nhưng thoái thác, chậm trễ.
+ Thường xuyên chậm deadline và có nhiều công việc tích tụ.
- Nguyên nhân dẫn đến việc trì hoãn:
+ Do bạn chưa thực sự tập trung và hết mình với công việc: chưa có ý thức sắp xếp, phân bố thời gian một cách hợp lý, làm việc gì cũng chậm chạp lề mề và coi việc chậm trễ là việc bình thường
+ Do xảy ra những việc biến động ngoài ý muốn mà chính bạn không lường trước được thì sẽ có thể làm gián đoạn buộc phải trì hoãn công việc
+ Do thói quen xấu khác (lười biếng, quyết tâm không cao, nuông chiều bản thân quá mức, dễ bị phân tâm bởi nhiều thứ khác ngoài công việc) khiến bạn cứ trì hoãn việc này sẽ ảnh hưởng đến tiến độ của việc khác, kế hoạch khác và không thể hoàn thành các nhiệm vụ đúng thời hạn
+ Do bạn thấy mình quá mệt mỏi, chán nản và không muốn thực hiện công việc theo kế hoạch.
+ Do bạn không biết bắt đầu công việc từ đâu nhưng không tìm hướng giải quyết.
+ Do bạn đã đánh giá sai về tính chất, thời gian cần thực hiện công việc.
+ Có thể do bạn quá chủ quan, quá tự tin vào khả năng bản thân và lãng phí thời gian.
+ Do bạn đó thói quen trì hoãn từ lâu nhưng không nhận ra và khắc phục.
+ Do bạn chịu ảnh hưởng từ những người xung quanh.
- Tác hại của thói quen trì hoãn: Trì hoãn công việc một lần có thể không sao nhưng nhiều lần thì có thể gây ảnh hưởng rất nhiều, trước là bản thân bạn và sau là những người xung quanh.
+ Gây lãng phí thời gian: Thử tưởng tượng xem nếu bạn hoàn thành công việc đúng thời hạn thì có thể làm thêm bao nhiêu công việc bổ ích nữa. Ngược lại, nếu luôn ở trong tình trạng “nước đến chân mới nhảy” thì bạn không chỉ gây lãng phí thời gian mà còn bỏ lỡ vô số việc quan trọng cần thực hiện.
+ Đánh mất nhiều cơ hội: Đánh mất những cơ hội quý báu cũng là một trong những tác hại của thói quen trì hoãn công việc gây ra. Theo đó, trong khoảng thời gian người khác đã hoàn thành công việc và nâng cao kỹ năng, tích lũy kinh nghiệm thì bạn mới khởi động. Và tất nhiên, khi họ về đích bạn mới đi được một phần nhỏ của hành trình.
+ Làm mất niềm tin và sự tôn trọng từ người khác: Sự sai lệch về thời gian do trì hoãn công việc cũng sẽ khiến bạn mất đi sự tôn trọng của người khác. Nói như vậy bởi không ai có thể cảm thông cho một người không tôn trọng cũng như chẳng thể tự thiết lập kỷ luật với chính bản thân mình. Trong cuộc sống, để có được niềm tin từ người khác là điều vô cùng khó. Do vậy, hãy trân trọng và đừng bao giờ để mọi người lo lắng, e ngại mỗi khi giao cho bạn bất kỳ công việc gì.
- Giải pháp khắc phục thói quen trì hoãn:
Để xóa tan được sự trì hoãn, các bạn có thể thực hiện theo 7 bước dưới đây:
+ Bước 1: Nhận thức bản thân đang trì hoãn. Trước hết, bạn cần phải biết gốc rễ của vấn đề rồi mới xử lý chúng. Mỗi nguyên nhân đều sẽ cần một cách tiếp cận và giải quyết khác nhau. Vậy nên, bạn cần nhận thức được rằng mình đang trì hoãn thì mới xóa tan được nó.
+ Bước 2: Tổ chức lại công việc: Bạn nên chia nhỏ các đầu việc như nghiên cứu, tạo outline, thực hiện chi tiết từng mục,… và tập trung riêng cho các tác vụ đó. Có một kế hoạch cụ thể sẽ giúp bạn theo dõi tiến độ, tuân thủ deadline và sửa chữa sai sót khi cần thiết. Nếu bạn cảm thấy công việc nhàm chán, hãy nhìn vào bức tranh tổng thể để thấy động lực làm việc.
+ Bước 3: Đặt mục tiêu: Thay vì mơ mộng về cái đích quá xa, bạn hãy đặt cho mình mục tiêu ngắn hạn, khả thi với từng giai đoạn. Điều này sẽ khiến công việc của bạn đỡ đáng sợ hơn đó.
+ Bước 4: Ngăn chặn yếu tố gây xao nhãng: Bạn hãy sắp xếp không gian làm việc thật gọn gàng, ngăn nắp, tắt hết chuông điện thoại, báo thức, đến những nơi yên tĩnh,…, bạn sẽ làm việc hiệu quả hơn rất nhiều.
+ Bước 5: Thưởng cho bản thân: Khi đã cố gắng làm việc, bạn đừng tiếc lời khen hay món quà cho bản thân mình. Bất kể mục tiêu bạn đạt được là lớn hay nhỏ, hãy để bản thân thư giãn một chút. Chẳng hạn sau mỗi tiến triển tốt trong công việc, bạn hãy tự mua món đồ mình thích. Khi bạn quan tâm đến mình, mọi thứ sẽ tốt đẹp và bạn sẽ có động lực để cố gắng hơn nữa.
+ Bước 6: Bạn cần rèn luyện những thói quen để tránh được sự trì hoãn: Thói quen quản lý thời gian / Thói quen tuân thủ kế hoạch / Ghi chú & gạch bỏ / Sử dụng quãng nghỉ ngắn / Giới hạn thời gian cho mỗi công việc
+ Bước 7: Đừng sợ thất bại: Bước cuối cùng, bạn hãy luôn nhìn vào những điều tích cực, đừng sợ thất bại. Việc học hỏi, đứng lên sau những vấp ngã cũng là một thành công. Thậm chí, nó giúp bạn nhận ra bản thân hợp với cái gì. Không có gì mình quyết tâm mà không mang lại lợi ích nào cả. Vì vậy, bạn đừng dung túng cho thói quen trì hoãn, hãy gạt nó đi và hành động ngay thôi!
c. Kết bài:
- Khẳng định lại vấn đề: Trì hoãn là một thói quen xấu và cần được bạn nhận thức/xóa bỏ để phát triển, cải thiện hay thay đổi bản thân. Đừng để thói quen trì hoãn trở thành vật cản con đường của hành trình đến với thành công của bạn
- Rút ra bài học cho bản thân: Là một người học sinh, bạn nên hiểu đúng về thói quen trì hoãn trong mọi việc, biết loại bỏ những biểu hiện tiêu cực nói trên để quản lí tốt thời gian và hình ảnh bản thân; cố gắng phấn đấu vươn lên để tự khẳng định những giá trị đích thực, bền vững… và tuyên truyền giúp đỡ mọi người cùng làm theo.