

Dương Lê Thảo Vy
Giới thiệu về bản thân



































Gọi số học sinh lần lượt ở khối 7,8,9 là x,y,z.
Ta có : \(\frac{a}{5} = \frac{b}{6} = \frac{c}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :\(\frac{a}{5} = \frac{b}{6} = \frac{c}{7} = \frac{b - a}{6 - 5} = \frac{50}{1} = 50\)
\(= > \frac{a}{5} = 50 = > a = 250\)
\(= > \frac{b}{6} = 50 = > b = 300\)
\(= > \frac{c}{7} = 50 = > c = 350\)
Vậy :.....................
Gọi số học sinh các khối 9, 8, 7, 6 lần lượt là \(x , y , z , t\)(học sinh) \(x , y , z , t \in N^{*}\).
Ta có: \(\frac{x}{9} = \frac{y}{8} = \frac{z}{7} = \frac{t}{6}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{9} = \frac{y}{8} = \frac{z}{7} = \frac{t}{6} = \frac{\left(\right. x + y \left.\right) - \left(\right. z + t \left.\right)}{\left(\right. 9 + 8 \left.\right) - \left(\right. 7 + 6 \left.\right)} = \frac{120}{4} = 30\)
\(\Leftrightarrow x = 30.9 = 270 , y = 30.8 = 240 , z = 30.7 = 210 , t = 30.6 = 180\)(thỏa mãn)
Gọi a,b,c lần lượt là số học sinh khối 6;7;8 (a,b,c: nguyên, dương)
Theo TC dãy tỉ số bằng nhau ta có:
\(\frac{a}{8} = \frac{b}{6} = \frac{c}{7} = \frac{c - b}{7 - 6} = \frac{15}{1} = 15\)
Vậy: a= 8 x 15= 120 => Số hs khối 6 là 120 học sinh
b= 6 x 15 = 90 => Số học sinh khối 7 là 90 học sinh
c= 7 x 15= 105 => Số hs khối 8 là 105 học sinh
x+1=\(\frac{5}{4} : \frac{1}{4}\)
x+1=5
x=5-1
x=4
B = \(\frac{1}{3}\) + \(\frac{1}{15}\) + \(\frac{1}{35}\) + ... + \(\frac{1}{97.99}\)
B = \(\frac{1}{1.3}\) + \(\frac{1}{3.5}\) + \(\frac{1}{5.7}\) + ... + \(\frac{1}{97.99}\)
B = \(\frac{1}{2} . \left(\right. \frac{2}{3.5} + \frac{2}{5.7} + \hdots + \frac{2}{97.99} \left.\right)\)
B = \(\frac{1}{2}\).(\(\frac{1}{3} - \frac{1}{5} + \frac{1}{5} - \frac{1}{7} + \hdots + \frac{1}{97} - \frac{1}{99} \left.\right)\)
B = \(\frac{1}{2} \left(\right. \frac{1}{3} - \frac{1}{99} \left.\right)\)
B = \(\frac{1}{2} \frac{. 32}{99}\)
B = \(\frac{16}{99}\)
Thể tích bể LÀ:
4 x 3 X 1,2 = 14,4(m\(^{3}\))
14,4m\(^{3}\) = 14400l
Lượng nước cần đổ vào bể bằng:
1 - \(\frac{3}{4} = \frac{1}{4}\) (bể)
Để bể đầy cần đổ thêm vào bể lượng nước là:
14 400 x \(\frac{1}{4}\) = 3600 (l)
Đáp số: 3600l
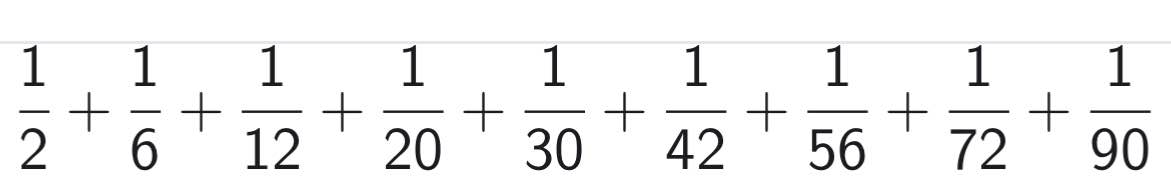
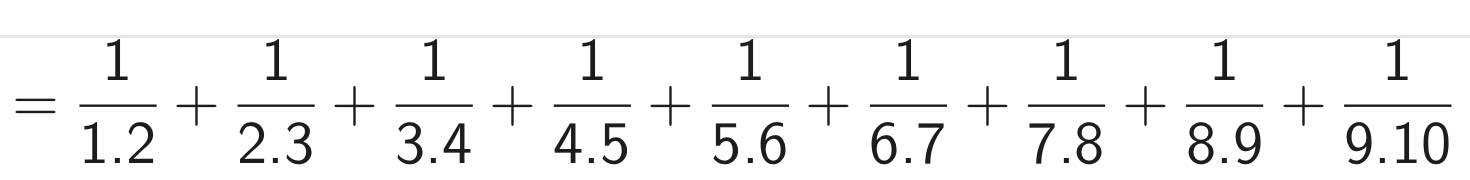
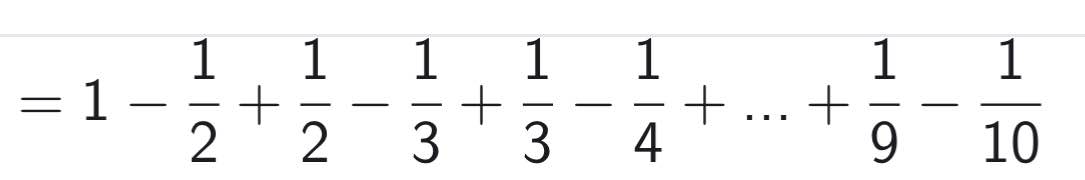
 =9phần10
=9phần10
Từ 𝑥−𝑦−𝑧=0⇒ {𝑥−𝑧=𝑦 𝑦−𝑥=−𝑧 𝑧+𝑦=𝑥x−y−z=0⇒ ⎩⎨⎧x−z=y y−x=−z z+y=x.
𝐵=(1−𝑧𝑥)(1−𝑥𝑦)(1+𝑦𝑧)=𝑥−𝑧𝑧.𝑦−𝑥𝑦.𝑧+𝑦𝑧=𝑦𝑥.−𝑧𝑦.𝑥𝑧=−1B=(1−xz)(1−yx)(1+zy)=zx−z.yy−x.zz+y=xy.y−z.zx=−1
Vậy 𝐵=−1B=−1.
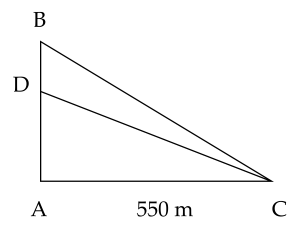 Gọi vị trí đặt loa là
Gọi vị trí đặt loa là
𝐷D suy ra 𝐷D nằm giữa 𝐴A và 𝐵B.Trong tam giác vuông 𝐴𝐷𝐶ADC ta có 𝐷𝐶DC là cạnh lớn nhất (đối diện với góc lớn nhất) nên 𝐷𝐶>𝐴𝐶=550DC>AC=550 m. Vậy tại 𝐶C không thể nghe tiếng loa, do vị trí 𝐶C đã nằm ngoài bán kính phát sóng của loa.
| GT |
Δ𝐴𝐵𝐶ΔABC vuông tại 𝐴A |
| KT |
a) Chứng minh Δ𝐴𝐵𝐷=Δ𝐸𝐵𝐷ΔABD=ΔEBD. |
a) Xét Δ𝐴𝐵𝐷ΔABD và Δ𝐸𝐵𝐷ΔEBD có
𝐵𝐴𝐷^=𝐵𝐸𝐷^=90∘BAD=BED=90∘ (gt)
𝐵𝐷BD là cạnh chung.
𝐴𝐵𝐷^=𝐸𝐵𝐷^ABD=EBD (gt).
Suy ra Δ𝐴𝐵𝐷=Δ𝐸𝐵𝐷ΔABD=ΔEBD (cạnh huyền - góc nhọn).
b) Chứng minh 𝐷𝐹>𝐷𝐴DF>DA mà 𝐷𝐴=𝐷𝐸DA=DE.
Từ đó suy ra 𝐷𝐹>𝐷𝐸DF>DE.