Đổi \(20\) phút \(= \frac{1}{3}\) h.

Gọi \(x\) là độ dài quãng đường từ thành phố về quê

Thời gian người đó đi từ thành phố về quê là: \(\frac{x}{30}\) km/h

Thời gian người đó đi từ quê lên thành phố là: \(\frac{x}{25}\) km/h

Vì thời gian lúc lên thành phố nhiều hơn thời gian về quê là \(20\) phút nên ta có phương trình:

\(\frac{x}{25} = \frac{x}{30} + \frac{1}{3}\)

\(\frac{5 x}{750} = \frac{1}{3}\)

\(15 x = 750\)

\(x = 50\) (thỏa mãn)

Vậy độ dài quãng đường từ thành phố về quê là \(50\) km

Vì \(B C\) là cạnh lớn nhất của tam giác nên \(\hat{B} , \hat{C} < 9 0^{\circ}\), do đó \(H\) nằm giữa \(B\) và \(C\).

Đặt \(H C = x , H B = y\), ta có : \(x + y = 21\) (1)

Mặt khác \(\left(A H\right)^{2} = 1 0^{2} - y^{2} , \left(A H\right)^{2} = 1 7^{2} - x^{2}\) nên \(x^{2} - y^{2} = 1 7^{2} - 1 0^{2} = 289 - 100 = 189\) (2)

Từ (1) và (2) suy ra \(x + y = 21\), \(x - y = 9\).

Do đó \(x = 15\), \(y = 6\).

Ta có \(\left(A H\right)^{2} = 1 0^{2} - 6^{2} = 64\) nên \(A H = 8\).

Vậy \(S_{A B C} = \frac{21.8}{2} = 84\) (cm\(^{2}\)).

Chiều cao của mỗi hình chóp tứ giác đều là:

     \(30 : 2 = 15\) (m).

Thể tích của lồng đèn quả trám là:

     \(V = 2. \left(\right. \frac{1}{3} . 20.20.15 \left.\right) = 4 000\) (cm\(^{3}\)).

Vì tam giác \(K B C\) vuông tại \(K\) suy ra \(\hat{K B H} = 9 0^{\circ}\)

Vì \(C I \bot B I\) (gt) suy ra \(\hat{C l H} = 9 0^{\circ}\)

Xét \(\triangle K B H\) và \(\triangle C H I\) có:

\(\hat{K B H} = \hat{C I H} = 9 0^{\circ}\);

\(\hat{B H K} = \hat{C H I}\) (đối đỉnh)

Suy ra \(\Delta B H K \sim \Delta C H I\) (g.g)

b) Ta có \(\Delta B H K \sim \Delta C H I\) suy ra \(\hat{H B K} = \hat{H C I}\) (hai góc tương ứng) 

Mà \(B H\) là tia phân giác của \(\hat{A B C}\) nên \(\hat{H B K} = \hat{H B C}\).

Do đó \(\hat{H B C} = \hat{H C I}\).

Xét \(\triangle C I B\) và \(\triangle H I C\) có:

\(\hat{C I B}\) chung;

\(\hat{I B C} = \hat{H C I}\) (cmt)

Vậy \(\Delta C I B \approx \Delta H I C\) (g.g) suy ra \(\frac{C I}{H I} = \frac{I B}{I C}\)

Hay \(\left(C I\right)^{2} = H I . I B\)

c) Xét \(\triangle A B C\) có \(B I \bot A C\); \(C K \bot A B\); \(B I \cap C K = \left{\right. H \left.\right}\)

Nên \(H\) là trực tâm \(\triangle A B C\) suy ra \(A H \bot B C\) tại \(D\).

Từ đó ta có \(\triangle B K C \sim \triangle H D C\) (g.g) nên \(\frac{C B}{C H} = \frac{C K}{C D}\)

Suy ra \(\frac{C B}{C K} = \frac{C H}{C D}\) nên \(\triangle B H C \sim \triangle K D C\) (c.g.c)

Khi đó \(\hat{H B C} = \hat{D K C}\) (hai góc tương ứng)

Chứng minh tương tự \(\hat{H A C} = \hat{I K C}\)

Mà \(\hat{H A C} = \hat{H B C}\) (cùng phụ \(\hat{A C B}\) )

Suy ra \(\&\text{nbsp}; \hat{D K C} = \hat{I K C}\).

Vậy \(K C\) là tia phân giác của \(\hat{I K D}\).

Có \(19\) kết quả cho hành động trên.

Có \(8\) kết quả thuận lợi cho biến cố đã cho nên xác suất cho biến cố là: \(\frac{8}{19}\).

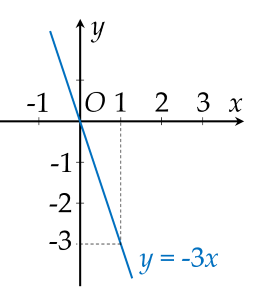
a) Xét đường thẳng: \(\left(\right. d_{1} \left.\right) : y = - 3 x\).

Nếu \(x = 0\) thì \(y = 0\) suy ra \(\left(\right. d_{1} \left.\right)\) đi qua điểm có tọa độ \(\left(\right. 0 ; 0 \left.\right)\)

Nếu \(x = 1\) thì \(y = - 3\) suy ra \(\left(\right. d_{1} \left.\right)\) đi qua điểm có tọa độ ( 1; -3 )

b) Vì \(\left(\right. d_{3} \left.\right) : y = a x + b\) song song với \(\left(\right. d_{2} \left.\right) : y = x + 2\) nên \(a = 1 , b \neq 2\).

Khi đó đường thẳng \(\left(\right. d_{3} \left.\right)\) có dạng \(y = x + b\) với \(b \neq 2\).

Vì \(\left(\right. d_{3} \left.\right)\) đi qua điểm có tọa độ \(A \left(\right. - 1 ; 3 \left.\right)\) nên: \(3 = - 1 + b\) hay \(b = 3 + 1 = 4\) (thỏa mãn).

Vậy đường thẳng \(\left(\right. d_{3} \left.\right)\) là \(\left(\right. d_{3} \left.\right) : y = - x + 4\)

a) \(2 x = 7 + x\)

\(2 x - x = 7\)

\(x = 7\)

b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\)

\(\frac{3 \left(\right. x - 3 \left.\right)}{15} + \frac{5. \left(\right. 1 + 2 x \left.\right)}{15} = 6\)

\(3 x - 9 + 5 + 10 x = 90\)

\(13 x = 94\)

\(x = \frac{94}{13}\).

a. Thiết lập và giải thích được công thức tính dữ liệu.

 Doanh thu theo tỉ lệ = (Địa chỉ tương đối) Tổng doanh thu * (Địa chỉ tuyệt đối) Tỉ lệ

Doanh thu thực = Doanh thu theo tỉ lệ - Chi phí khác 

c. Tiêu chí sắp xếp dữ liệu

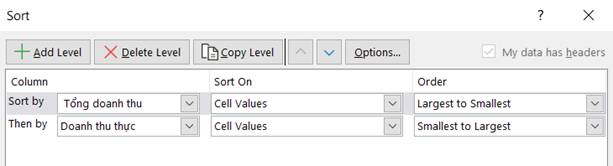
Kết quả sau sắp xếp như sau.

d. Sử dụng Number Filters với điều kiện lọc Greater than…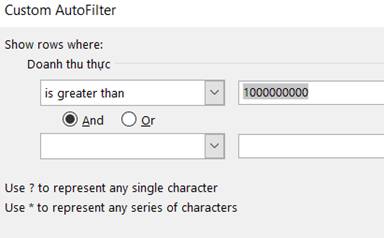

Kết quả sau sắp xếp như bảng sau đây.

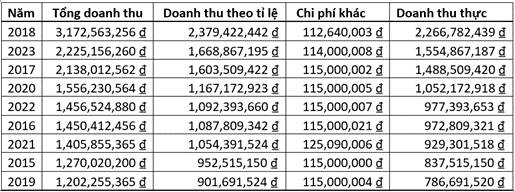
Việc tự do đăng tải hình ảnh trên mạng xã hội mà không tuân thủ các tiêu chuẩn đạo đức và quy định pháp luật có thể xuất phát từ nhiều nguyên nhân khác nhau. Một số trong đó gồm:

Nguyên nhân:

- Nhiều người chưa hiểu rõ về hậu quả của việc đăng tải hình ảnh không phù hợp và các quy định pháp luật liên quan

- Người đăng tải có thể muốn kiếm lợi từ việc lan truyền hình ảnh, như quảng cáo, tiếp thị, hoặc xây dựng thương hiệu cá nhân mà không nghĩ đến hậu quả

- Sự thiếu chặt chẽ trong việc quản lý nội dung trên mạng xã hội cũng có thể khiến người dùng dễ dàng đăng tải các hình ảnh không phù hợp

Tác hại:

- Hình ảnh không phù hợp có thể gây tổn hại đến danh dự, uy tín của cá nhân hoặc tổ chức

- Hành vi này có thể dẫn đến các hệ quả pháp lý như bị phạt tiền, thậm chí chịu trách nhiệm hình sự

- Việc lan truyền nội dung không phù hợp có thể ảnh hưởng đến văn hóa trực tuyến và làm giảm chất lượng của môi trường mạng xã hội

- Các hình ảnh không phù hợp có thể gây ảnh hưởng tiêu cực đến tâm lý của người xem, đặc biệt là trẻ em và thanh thiếu niên