

Phạm Duy Khánh
Giới thiệu về bản thân



































Xét \(\Delta A B C\) có \(A B = 10\) cm, \(A C = 17\) cm, \(B C = 21\) cm.
Gọi \(A H\) là đường cao của tam giác.

Vì \(B C\) là cạnh lớn nhất của tam giác nên \(\hat{B} , \hat{C} < 9 0^{\circ}\), do đó \(H\) nằm giữa \(B\) và \(C\).
Đặt \(H C = x , H B = y\), ta có : \(x + y = 21\) (1)
Mặt khác \(\left(A H\right)^{2} = 1 0^{2} - y^{2} , \left(A H\right)^{2} = 1 7^{2} - x^{2}\) nên \(x^{2} - y^{2} = 1 7^{2} - 1 0^{2} = 289 - 100 = 189\) (2)
Từ (1) và (2) suy ra \(x + y = 21\), \(x - y = 9\).
Do đó \(x = 15\), \(y = 6\).
Ta có \(\left(A H\right)^{2} = 1 0^{2} - 6^{2} = 64\) nên \(A H = 8\).
Vậy \(S_{A B C} = \frac{21.8}{2} = 84\) (cm\(^{2}\)).
Xét \(\Delta A B C\) có \(A B = 10\) cm, \(A C = 17\) cm, \(B C = 21\) cm.
Gọi \(A H\) là đường cao của tam giác.

Vì \(B C\) là cạnh lớn nhất của tam giác nên \(\hat{B} , \hat{C} < 9 0^{\circ}\), do đó \(H\) nằm giữa \(B\) và \(C\).
Đặt \(H C = x , H B = y\), ta có : \(x + y = 21\) (1)
Mặt khác \(\left(A H\right)^{2} = 1 0^{2} - y^{2} , \left(A H\right)^{2} = 1 7^{2} - x^{2}\) nên \(x^{2} - y^{2} = 1 7^{2} - 1 0^{2} = 289 - 100 = 189\) (2)
Từ (1) và (2) suy ra \(x + y = 21\), \(x - y = 9\).
Do đó \(x = 15\), \(y = 6\).
Ta có \(\left(A H\right)^{2} = 1 0^{2} - 6^{2} = 64\) nên \(A H = 8\).
Vậy \(S_{A B C} = \frac{21.8}{2} = 84\) (cm\(^{2}\)).
Chiều cao của mỗi hình chóp tứ giác đều là:
\(30 : 2 = 15\) (m).
Thể tích của lồng đèn quả trám là:
\(V = 2. \left(\right. \frac{1}{3} . 20.20.15 \left.\right) = 4 000\) (cm\(^{3}\)).
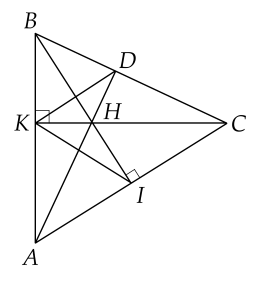
a) Vì tam giác \(K B C\) vuông tại \(K\) suy ra \(\hat{K B H} = 9 0^{\circ}\)
Vì \(C I \bot B I\) (gt) suy ra \(\hat{C l H} = 9 0^{\circ}\)
Xét \(\triangle K B H\) và \(\triangle C H I\) có:
\(\hat{K B H} = \hat{C I H} = 9 0^{\circ}\);
\(\hat{B H K} = \hat{C H I}\) (đối đỉnh)
Suy ra \(\Delta B H K \sim \Delta C H I\) (g.g)
b) Ta có \(\Delta B H K \sim \Delta C H I\) suy ra \(\hat{H B K} = \hat{H C I}\) (hai góc tương ứng)
Mà \(B H\) là tia phân giác của \(\hat{A B C}\) nên \(\hat{H B K} = \hat{H B C}\).
Do đó \(\hat{H B C} = \hat{H C I}\).
Xét \(\triangle C I B\) và \(\triangle H I C\) có:
\(\hat{C I B}\) chung;
\(\hat{I B C} = \hat{H C I}\) (cmt)
Vậy \(\Delta C I B \approx \Delta H I C\) (g.g) suy ra \(\frac{C I}{H I} = \frac{I B}{I C}\)
Hay \(\left(C I\right)^{2} = H I . I B\)
c) Xét \(\triangle A B C\) có \(B I \bot A C\); \(C K \bot A B\); \(B I \cap C K = \left{\right. H \left.\right}\)
Nên \(H\) là trực tâm \(\triangle A B C\) suy ra \(A H \bot B C\) tại \(D\).
Từ đó ta có \(\triangle B K C \sim \triangle H D C\) (g.g) nên \(\frac{C B}{C H} = \frac{C K}{C D}\)
Suy ra \(\frac{C B}{C K} = \frac{C H}{C D}\) nên \(\triangle B H C \sim \triangle K D C\) (c.g.c)
Khi đó \(\hat{H B C} = \hat{D K C}\) (hai góc tương ứng)
Chứng minh tương tự \(\hat{H A C} = \hat{I K C}\)
Mà \(\hat{H A C} = \hat{H B C}\) (cùng phụ \(\hat{A C B}\) )
Suy ra \(\&\text{nbsp}; \hat{D K C} = \hat{I K C}\).
Vậy \(K C\) là tia phân giác của \(\hat{I K D}\).
Có \(19\) kết quả cho hành động trên.
Có \(8\) kết quả thuận lợi cho biến cố đã cho nên xác suất cho biến cố là: \(\frac{8}{19}\).
Bài 1. (1 điểm) Giải các phương trình sau:
a) \(2 x = 7 + x\).
b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\).
Hướng dẫn giải:
a) \(2 x = 7 + x\)
\(2 x - x = 7\)
\(x = 7\).
Phương trình đã cho có nghiệm \(x = 7\).
b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\)
\(\frac{3 \left(\right. x - 3 \left.\right)}{15} + \frac{5. \left(\right. 1 + 2 x \left.\right)}{15} = 6\)
\(3 x - 9 + 5 + 10 x = 90\)
\(13 x = 94\)
\(x = \frac{94}{13}\).
Phương trình đã cho có nghiệm \(x = \frac{94}{13}\).
(x2+y2)24x2y2−1+y2x2+x2y2−2≥0
\(\frac{4 x^{2} y^{2} - \left(\right. x^{2} + y^{2} \left.\right)^{2}}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} + \frac{x^{4} + y^{4} - 2 x^{2} y^{2}}{x^{2} y^{2}} \geq 0\)
\(\frac{- \left(\right. x^{2} - y^{2} \left.\right)^{2}}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} + \frac{\left(\right. x^{2} - y^{2} \left.\right)^{2}}{x^{2} y^{2}} \geq 0\)
\(\left(\right. x^{2} - y^{2} \left.\right)^{2} . \left[\right. \frac{1}{x^{2} y^{2}} - \frac{1}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} \&\text{nbsp}; \left]\right. \geq 0\)
\(\left(\right. x^{2} - y^{2} \left.\right)^{2} . \frac{\left(\right. x^{2} + y^{2} \left.\right)^{2} - x^{2} y^{2}}{x^{2} y^{2} \left(\right. x^{2} + y^{2} \left.\right)^{2}} \geq 0\)
\(\left(\right. x^{2} - y^{2} \left.\right)^{2} . \frac{x^{4} + y^{4} + x^{2} y^{2}}{x^{2} y^{2} \left(\right. x^{2} + y^{2} \left.\right)^{2}} \geq 0\).
Dấu bằng xảy ra khi và chỉ khi \(x = y\) hoặc \(x = - y\).
Chứng minh được: \(\Delta ABC\sim\Delta HBA\) (g.g)
Từ đó suy ra \(A B^{2} = B C . B H\)
\(\hat{A E D} = \hat{A D E}\) (Cùng phụ với \(\hat{A B D} = \hat{C B D}\))
Suy ra \(\Delta A E D\) cân tại \(A\) suy ra \(A I\) vuông góc với \(D E\) tại \(I\).
Chứng minh \(\Delta E H B\) và \(\Delta E I A\) đồng dạng (g.g).
Từ đó suy ra \(\frac{E I}{E H} = \frac{E A}{E B}\) nên \(E I . E B = E H . E A\).
Gọi \(x\) (km) là quãng đường \(A B\).
Điều kiện: \(x > 0\).
Thời gian người đó đi xe đạp từ \(A\) đến \(B\) là: \(\frac{x}{15}\) (h);
Thời gian lúc về của người đó là: \(\frac{x}{12}\) (h).
Vì thời gian về nhiều hơn thời gian đi \(45\) phút \(= \frac{3}{4}\) (h), nên ta có phương trình:
\(\frac{x}{12} - \frac{x}{15} = \frac{3}{4}\)
\(\frac{5 x}{60} - \frac{4 x}{60} = \frac{45}{60}\)
\(5 x - 4 x = 45\)
\(x = 45\) (TMĐK)
Vậy quãng đường \(A B\) dài \(45\) (km).
a) \(A = \frac{3 x + 15}{x^{2} - 9} + \frac{1}{x + 3} - \frac{2}{x - 3}\) (với \(x \neq 3\), \(x \neq - 3\))
\(A = \frac{3 x + 15}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)} + \frac{1}{x + 3} - \frac{2}{x - 3}\)
\(A = \frac{3 x + 15 + x - 3 - 2 x - 6}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)
\(A = \frac{2 x + 6}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)
\(A = \frac{2}{x - 3}\).
b) Để \(A = \frac{2}{3}\) thì \(\frac{2}{x - 3} = \frac{2}{3}\)
\(x - 3 = 3\)
\(x = 6\) (thỏa mãn điều kiện).
Vậy \(x = 6\) thì \(A = \frac{2}{3}\).