

Lê Minh Phúc
Giới thiệu về bản thân



































2(10+17+21)=24(cm)
Diện tích tam giác:
\(� = \sqrt{24. \left(\right. 24 - 10 \left.\right) . \left(\right. 24 - 17 \left.\right) . \left(\right. 24 - 21 \left.\right)} = 84 \left(\right. � �^{2} \left.\right)\)
Chiều cao của mỗi hình chóp tứ giác đều là:
30:2=1530:2=15 (m).
Thể tích của lồng đèn quả trám là:
𝑉=2.(13.20.20.15)=4000V=2.(31.20.20.15)=4000 (cm33).

a) Xét hai tam giác vuông: \(\Delta � � �\) và \(\Delta � � �\) có:
\(\hat{� � �} = \hat{� � �}\) (đối đỉnh)
\(\Rightarrow \Delta � � �\) ∽ \(\Delta � � � \left(\right. � - � \left.\right)\)
b) Do \(� �\) là tia phân giác của \(\hat{� � �}\) (gt)
\(\Rightarrow \hat{� � �} = \hat{� � �}\)
\(\Rightarrow \hat{� � �} = \hat{� � �}\) (1)
Do \(\Delta � � �\) ∽ \(\Delta � � � \left(\right. � � � \left.\right)\)
\(\Rightarrow \hat{� � �} = \hat{� � �}\) (2)
Từ (1) và (2) \(\Rightarrow \hat{� � �} = \hat{� � �}\)
Xét hai tam giác vuông: \(\Delta � � �\) và \(\Delta � � �\) có:
\(\hat{� � �} = \hat{� � �} \left(\right. � � � \left.\right)\)
\(\Rightarrow \Delta � � �\) ∽ \(\Delta � � � \left(\right. � - � \left.\right)\)
\(\Rightarrow \frac{� �}{� �} = \frac{� �}{� �}\)
\(\Rightarrow � �^{2} = � � . � �\)
c) Do \(� � \bot � �\) tại \(�\) (gt)
\(\Rightarrow � � \bot � �\)
\(\Rightarrow � �\) là đường cao của \(\Delta � � �\)
Lại có:
\(� � \bot � � \left(\right. � � \left.\right)\)
\(\Rightarrow � � \bot � �\)
\(\Rightarrow � �\) là đường cao thứ hai của \(\Delta � � �\)
Mà H là giao điểm của \(� �\) và \(� �\) (gt)
\(\Rightarrow � �\) là đường cao thứ ba của \(\Delta � � �\)
\(\Rightarrow � � \bot � �\)
Xét hai tam giác vuông: \(\Delta � � �\) và \(\Delta � � �\) có:
\(� �\) là cạnh chung
\(\hat{� � �} = \hat{� � �}\) (do BH là tia phân giác của \(\hat{�}\))
\(\Rightarrow \Delta � � � = \Delta � � �\) (cạnh huyền - góc nhọn)
\(\Rightarrow � � = � �\) (hai cạnh tương ứng)
\(\Rightarrow �\) nằm trên đường trung trực của DK (3)
Do \(\Delta � � � = \Delta � � � \left(\right. � � � \left.\right)\)
\(\Rightarrow � � = � �\) (hai cạnh tương ứng)
\(\Rightarrow �\) nằm trên đường trung trực của DK (4)
Từ (3) và (4) \(\Rightarrow � �\) là đường trung trực của DK
\(\Rightarrow \hat{� � �} + \hat{� � �} = 9 0^{0}\)
Mà \(\hat{� � �} = \hat{� � �}\) (cmt)
\(\Rightarrow \hat{� � �} + \hat{� � �} = 9 0^{0}\) (*)
\(\Delta � � �\) có:
\(� �\) là đường phân giác (cmt)
\(� �\) cũng là đường cao (cmt)
\(\Rightarrow \Delta � � �\) cân tại B
\(\Rightarrow � �\) là đường trung trực của \(\Delta � � �\)
\(\Rightarrow �\) là trung điểm của AC
\(\Rightarrow � �\) là đường trung tuyến của \(\Delta � � �\)
\(\Delta � � �\) vuông tại K có KI là đường trung tuyến ứng với cạnh huyền AC
\(\Rightarrow � � = � � = � � = \frac{� �}{2}\)
\(\Rightarrow \Delta � � �\) cân tại \(�\)
\(\Rightarrow \hat{� � �} = \hat{� � �}\)
\(\Rightarrow \hat{� � �} = \hat{� � �}\)
Mà \(\hat{� � �} + \hat{� � �} = 9 0^{0}\)
\(\Rightarrow \hat{� � �} + \hat{� � �} = 9 0^{0}\) (**)
Từ (*) và (**) \(\Rightarrow \hat{� � �} = \hat{� � �}\)
\(\Rightarrow � �\) là tia phân giác của \(\hat{� � �}\)
Hay \(� �\) là tia phân giác của \(\hat{� � �}\)
Đúng(1) PM Phan Minh Ngọc 21 tháng 5 2024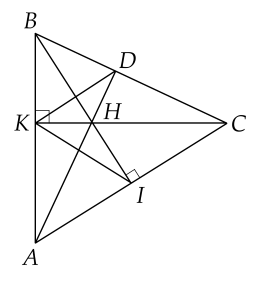
a) Vì tam giác 𝐾𝐵𝐶KBC vuông tại 𝐾K suy ra 𝐾𝐵𝐻^=90∘KBH=90∘
Vì 𝐶𝐼⊥𝐵𝐼CI⊥BI (gt) suy ra 𝐶𝑙𝐻^=90∘ClH=90∘
Xét △𝐾𝐵𝐻△KBH và △𝐶𝐻𝐼△CHI có:
𝐾𝐵𝐻^=𝐶𝐼𝐻^=90∘KBH=CIH=90∘;
𝐵𝐻𝐾^=𝐶𝐻𝐼^BHK=CHI (đối đỉnh)
Suy ra Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI (g.g)
b) Ta có Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI suy ra 𝐻𝐵𝐾^=𝐻𝐶𝐼^HBK=HCI (hai góc tương ứng)
Mà 𝐵𝐻BH là tia phân giác của 𝐴𝐵𝐶^ABC nên 𝐻𝐵𝐾^=𝐻𝐵𝐶^HBK=HBC.
Do đó 𝐻𝐵𝐶^=𝐻𝐶𝐼^HBC=HCI.
Xét △𝐶𝐼𝐵△CIB và △𝐻𝐼𝐶△HIC có:
𝐶𝐼𝐵^CIB chung;
𝐼𝐵𝐶^=𝐻𝐶𝐼^IBC=HCI (cmt)
Vậy Δ𝐶𝐼𝐵≈Δ𝐻𝐼𝐶ΔCIB≈ΔHIC (g.g) suy ra 𝐶𝐼𝐻𝐼=𝐼𝐵𝐼𝐶HICI=ICIB
Hay 𝐶𝐼2=𝐻𝐼.𝐼𝐵CI2=HI.IB
c) Xét △𝐴𝐵𝐶△ABC có 𝐵𝐼⊥𝐴𝐶BI⊥AC; 𝐶𝐾⊥𝐴𝐵CK⊥AB; 𝐵𝐼∩𝐶𝐾={𝐻}BI∩CK={H}
Nên 𝐻H là trực tâm △𝐴𝐵𝐶△ABC suy ra 𝐴𝐻⊥𝐵𝐶AH⊥BC tại 𝐷D.
Từ đó ta có △𝐵𝐾𝐶∽△𝐻𝐷𝐶△BKC∽△HDC (g.g) nên 𝐶𝐵𝐶𝐻=𝐶𝐾𝐶𝐷CHCB=CDCK
Suy ra 𝐶𝐵𝐶𝐾=𝐶𝐻𝐶𝐷CKCB=CDCH nên △𝐵𝐻𝐶∽△𝐾𝐷𝐶△BHC∽△KDC (c.g.c)
Khi đó 𝐻𝐵𝐶^=𝐷𝐾𝐶^HBC=DKC (hai góc tương ứng)
Chứng minh tương tự 𝐻𝐴𝐶^=𝐼𝐾𝐶^HAC=IKC
Mà 𝐻𝐴𝐶^=𝐻𝐵𝐶^HAC=HBC (cùng phụ 𝐴𝐶𝐵^ACB )
Suy ra 𝐷𝐾𝐶^=𝐼𝐾𝐶^ DKC=IKC.
Vậy 𝐾𝐶KC là tia phân giác của 𝐼𝐾𝐷^IKD.
Đúng(0) Xem thêm câu trả lời Các câu hỏi dưới đây có thể giống với câu hỏi trên HK huy khổng 15 tháng 6 2017 - olm cho tam giác ABC vuông tại C (AC<BC). vẽ tia phân giác Ax của góc BAC cắt cạnh BC tại I. qua B vẽ đường vuông góc với tia Ax và cắt tia Ax tại H.a) chứng minh tam giác AIC đồng dạng với tam giác BHI.b) cho AC=15cm,AB=25cm. tính độ dài các cạnh CB, Ci ?c) chứng minh HB^2 =Hi.HAd) gọi k là trung điểm của cạnh AB. qua i vẽ đường thẳng vuông góc với iK và cắt hai cạnh AC và BH lần lượt tại M và N chứng minh... Đọc tiếp #Hỏi cộng đồng OLM#Toán lớp 8 0 LM ND Nguyễn Đức Tuyên 12 tháng 2 2022 #Hỏi cộng đồng OLM#Toán lớp 8 0 LM NH nguyễn Hữu Bẩy 5 tháng 1 2018 - olm Bài 3: (3,5 điểm) Cho ΔABC vuông tại C (AC < BC). Vẽ tia phân giác Ax của cắt cạnh BC tại I. Qua B vẽ đường thẳng vuông góc với tia Ax và cắt tia Ax tại H.a. Chứng minh: ΔAIC đồng dạng với ΔBHI.b. Cho AC = 15cm, AB = 25cm. Tính độ dài các cạnh CB, CI?c. Chứng minh: HB2 = HI.HA.d. Gọi K là trung điểm của cạnh AB.Qua I vẽ đường thẳng vuông góc với IK và cắt hai cạnh AC và BH lần lượt tại M và N.... Đọc tiếp #Hỏi cộng đồng OLM#Toán lớp 8 3 LM CB Come Back Jack 7 tháng 5 2020eo biet vi lop 5
Đúng(0) UL Uyên Linh cute 7 tháng 5 2020mik ko biết
Đúng(0) Xem thêm câu trả lời HD HOÀNG ĐỨC VIỆT 4 tháng 4 2018 - olm #Hỏi cộng đồng OLM#Toán lớp 8 0 LM PT Phan thị cẩm nhung 6 tháng 7 2019 - olm Cho tam giác ABC vuông tại A (AB<AC). Vẽ đường cao AH (H thuộc BC). Gọi D là điểm đối xứng với B qua Ha) chứng minh tam giác ABC đồng dạng vs tam giác HBAb) từ C kẻ đường thẳng vuông góc vs tia AD, cắt AD tại E. Chứng minh AH.CD=CE.ADc) chứng minh tam giác ABC đồng dạng vs tam giác EDC và tính diện tích tam giác EDC bt AB=6cm, AC=8cmd) bt AH cắt CE tại E, tia FD cắt AC tại K. Chứng minh KD là tia phân giác góc... Đọc tiếp #Hỏi cộng đồng OLM#Toán lớp 8 0 LM D dũng 16 tháng 4 2023 Cho tam giác ABC vuông tại A( AB<AC), đường cao AH. Lấy điểm I thuộc cạnh AH. Kẻ đường thẳng đi qua B và vuông góc CI tại K. a) Chứng minh rằng CH.CB=CI.CK b) Tia BK cắt tia HA tại D. Chứng minh rằng góc BHK= góc BDC. c) Trên tia đối của tia KC lấy điểm M sao cho BM=BA. Chứng minh rằng góc BMD= 90 độ d) Vẽ đường phân giác AN của tam giác ABC ( N thuộc BC ) ; đường phân giác NE ( E thuộc BC ) ; đường phân... Đọc tiếp #Hỏi cộng đồng OLM#Toán lớp 8 1 LM NL Nguyễn Lê Phước Thịnh 16 tháng 4 2023a: Xét ΔCKB vuông tại K và ΔCHI vuông tại H có
góc KCB chung
=>ΔCKB đồng dạng với ΔCHI
=>CK/CH=CB/CI
=>CK*CI=CH*CB=CA^2
b: Xét ΔBHD vuông tại H và ΔBKC vuông tại K có
góc KBC chung
=>ΔBHD đồng dạng với ΔBKC
=>BH/BK=BD/BC
=>BD*BK=BH*BC=BA^2
c: BA^2=BD*BK
BA=BM
=>BM^2=BD*BK
=>ΔBMD vuông tại M
=>góc BMD=90 độ
d: SỬa đề: EA/EB*NB/NC*FC/FA
=NA/NB*NB/NC*NC/NA
=1
Đúng(0) NL Ngọc Lan 14 tháng 7 2017 - olm #Hỏi cộng đồng OLM#Toán lớp 8 0 LM BT bảo trân lê 8 tháng 5 2019 - olma) Tam Giác AKH đồng dạng với tam giác AMB và tam giác ABH đồng dạng với tam giác AMK.
Mình cần câu c thôi ạ, gấp. Cảm ơn!
#Hỏi cộng đồng OLM#Toán lớp 8 0 LM TL Tạ Liên Hoa 28 tháng 4 2022giúp mình với, mình cần ngay bây giờ
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABC\(sim\)ΔHBA
b: Xét ΔCAI vuông tại A và ΔCHK vuông tại H có
\(\hat{� � �} = \hat{� � �}\)
Do đó: ΔCAI\(sim\)ΔCHK
SUy ra: CA/CH=CI/CK
hay \(� � \cdot � � = � � \cdot � �\)
Đúng(0) LQ Lê Quang Hiếu 25 tháng 3 2018 - olma) Tam Giác AKH đồng dạng với tam giác AMB và tam giác ABH đồng dạng với tam giác AMK.
#Hỏi cộng đồng OLM#Toán lớp 8 0 LM Xếp hạng- Tuần
- Tháng
- Năm
- DH Đỗ Hoàn VIP 40 GP
- GN GV Nguyễn Trần Thành Đạt 4 GP
- PK Phạm Khánh Linh 2 GP
- NH Nguyễn Hữu Minh Hiếu 2 GP
- BH Bui Hanh Nguyen VIP 2 GP
- CL Chau Le To Minh 2 GP
- VM Vũ Minh Hoàng VIP 2 GP
- TT Trần Thị Hồng Giang 0 GP
- NV Nguyễn Vũ Thu Hương 0 GP
- HA Hải Anh ^_^ 0 GP
Gọi A là biến cố "Lấy được viên bi màu đỏ"
Trong túi có 8 viên màu đỏ nên n(A)=8
=>\(P\left(A\right.\left.\right)=\frac{8}{19}\)
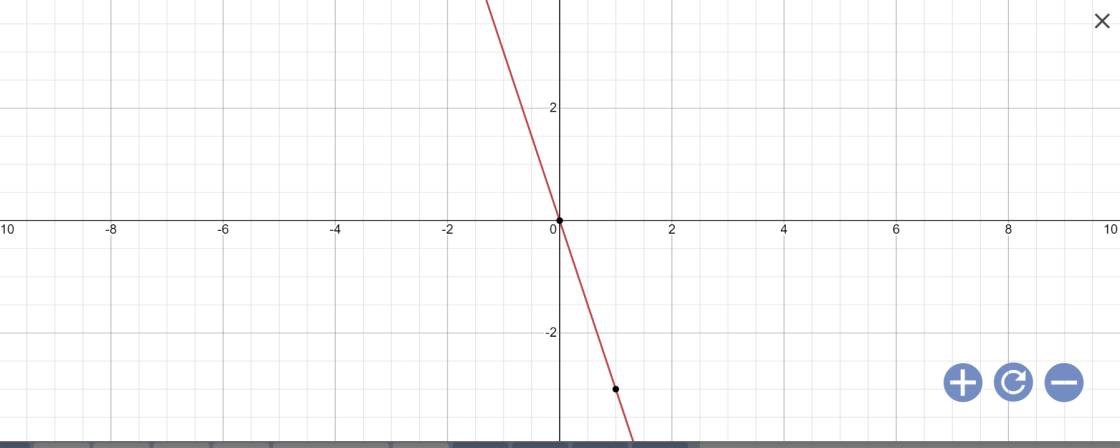 b: Vì (d3)//(d2) nên \(\left{\right. � = 1 \\ � \neq 2\)
b: Vì (d3)//(d2) nên \(\left{\right. � = 1 \\ � \neq 2\)
Vậy: (d3): y=x+b
Thay x=-1 và y=3 vào (d3), ta được:
b-1=3
=>b=4
Vậy: (d3): y=x+4
Bài 2:
Gọi số sản phẩm tổ 1 phải sản xuất theo kế hoạch là x(sản phẩm)
(ĐIều kiện: \(� \in �^{+}\))
Số sản phẩm tổ 2 phải sản xuất theo kế hoạch là:
900-x(sản phẩm)
Số sản phẩm thực tế tổ 1 làm được là:
\(� \left(\right. 1 + 20 \% \left.\right) = 1 , 2 � \left(\right. � ả � � ℎ ẩ � \left.\right)\)
Số sản phẩm thực tế tổ 2 làm được là:
\(\left(\right. 900 - � \left.\right) \left(\right. 1 + 15 \% \left.\right) = 1 , 15 \left(\right. 900 - � \left.\right) \left(\right. � ả � � ℎ ẩ � \left.\right)\)
Tổng số sản phẩm là 1055 sản phẩm nên ta có:
1,2x+1,15(900-x)=1055
=>0,05x+1035=1055
=>0,05x=20
=>x=400(nhận)
Vậy: số sản phẩm tổ 1 phải sản xuất theo kế hoạch là 400 sản phẩm
số sản phẩm tổ 2 phải sản xuất theo kế hoạch là 900-400=500 sản phẩm

Ta có: 𝑥−𝑎𝑏𝑐+𝑥−𝑏𝑐𝑎+𝑥−𝑐𝑎𝑏=2𝑎+2𝑏+2𝑐bcx−a+cax−b+abx−c=a2+b2+c2
(𝑥−𝑎𝑏𝑐−2𝑎)+(𝑥−𝑏𝑐𝑎−2𝑏)+(𝑥−𝑐𝑎𝑏−2𝑐)=0(bcx−a−a2)+(cax−b−b2)+(abx−c−c2)=0
𝑎(𝑥−𝑎)−2𝑏𝑐+𝑏(𝑥−𝑏)−2𝑐𝑎+𝑐(𝑥−𝑐)−2𝑎𝑏𝑎𝑏𝑐=0abca(x−a)−2bc+b(x−b)−2ca+c(x−c)−2ab=0
Điều kiện xác định: 𝑎,𝑏,𝑐≠0a,b,c=0
Khi đó: (𝑎+𝑏+𝑐)𝑥−𝑎2−2𝑏𝑐−𝑏2−2𝑐𝑎−𝑐2−2𝑎𝑏𝑎𝑏𝑐=0abc(a+b+c)x−a2−2bc−b2−2ca−c2−2ab=0
(𝑎+𝑏+𝑐)𝑥=(𝑎+𝑏+𝑐)2(a+b+c)x=(a+b+c)2
+ Nếu 𝑎+𝑏+𝑐=0a+b+c=0 thì phương trình có vô số nghiệm.
+ Nếu 𝑎+𝑏+𝑐≠0a+b+c=0 thì phương trình có nghiệm duy nhất 𝑥=𝑎+𝑏+𝑐x=a+b+c.



\(\) \(\)

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)
20 phút = 1/3 h
Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)
Quãng đường đi từ thành phố về quê: 30x (km)
Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)
Theo đề bài, ta có phương trình:
30x = 25(x + 1/3)
30x = 25x + 25/3
30x - 25x = 25/3
5x = 25/3
x = 25/3 : 5
x = 5/3 (nhận)
Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km