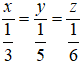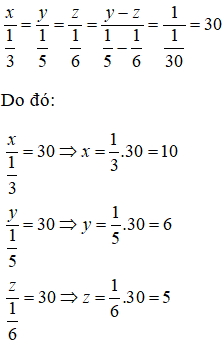Trần Đức Hải
Giới thiệu về bản thân



































Tam giác ABC cân tại A nên B^B = C^C
⇒ ABM^ABM = ACN^ACN (1)
AB = AC (2)
BAM^BAM = CAN^CAN = 900 (3)
Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)
b, BM = CN ( Δ BAM = ΔCAN)
BM = BN + MN = MN + MC
⇒ BN = CM
c, BAN^BAN + NAC^NAC = BAC^BAC =1200
⇒⇒ BAN^BAN = 1200 - NAC^NAC = 1200 - 900 = 300
ABN^ABN = (1800 - 1200) : 2 = 300
⇒ BAN^BAN = ABN^ABN = 300 ⇒ △ANB cân tại N
Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của các đội 1, 2, 3 (điều kiện x, y, z ∈ N*)
Vì diện tích các cánh đồng là như nhau nên số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, suy ra 3x = 5y = 6z.
Đội thứ hai nhiều hơn đội thứ ba 1 máy nên y – z = 1.
Từ 3x = 5y = 6z, suy ra
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Vậy đội 1 có 10 máy cày, đội hai có 6 máy và đội 3 có 5 máy
Ta có P(x)−Q(x)=(x3−3x2+x+1)−(2x3−x2+3x−4)P(x)−Q(x)=(x3−3x2+x+1)−(2x3−x2+3x−4)
=x3−3x2+x+1−2x3+x2−3x+4=x3−3x2+x+1−2x3+x2−3x+4
=−x3−2x2−2x+5=−x3−2x2−2x+5.
b) Thay x=1x=1 vào hai đa thức ta có:
P(1)= 13−3.12+1+1=0P(1)= 13−3.12+1+1=0
Q(1)= 2.13−12+3.1−4=0Q(1)= 2.13−12+3.1−4=0
Vậy x=1x=1 là nghiệm của cả hai đa thức P(x)P(x) và Q(x)Q(x).
a) x=-22. b)x1=0. x2=16