

Lương Hoàng Phúc
Giới thiệu về bản thân



































Tại x=9x=9 thì:
C=x14−10x13+10x12−10x11+...+10x2−10x+10C=x14−10x13+10x12−10x11+...+10x2−10x+10
C=x14−(x+1)x13+(x+1)x12−(x+1)x11+...+(x+1)x2−(x+1)x+x+1C=x14−(x+1)x13+(x+1)x12−(x+1)x11+...+(x+1)x2−(x+1)x+x+1
C=x14−x14−x13+x13+x12−x12−x11+...+x3+x2−x2−x+x+1C=x14−x14−x13+x13+x12−x12−x11+...+x3+x2−x2−x+x+1
C=1C=1.
Vậy tại x=9x=9 thì giá trị của CC bằng 11.
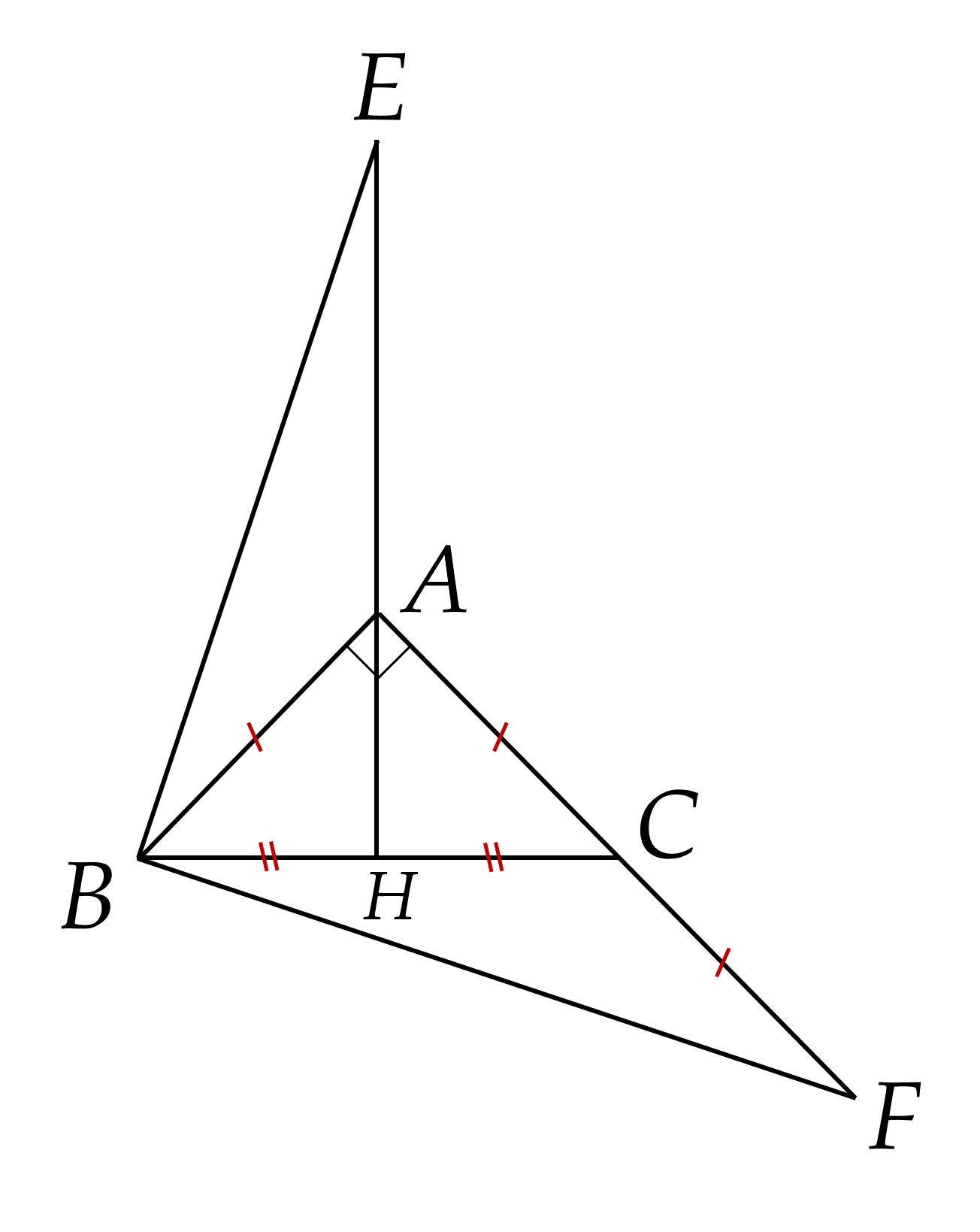
a) Xét ΔAHBΔAHB và ΔAHCΔAHC có:
AB=ACAB=AC (gt);
AHAH chung;
HB=HCHB=HC (HH là trung điểm của BCBC);
Suy ra ΔAHB=ΔAHCΔAHB=ΔAHC (c.c.c).
b) Vì ΔAHB=ΔAHCΔAHB=ΔAHC (cmt) suy ra AHB^=AHC^AHB=AHC (cặp góc tương ứng).
Mà AHB^+AHC^=180∘AHB+AHC=180∘ (hai góc kề bù).
Suy ra AHB^=AHC^=90∘AHB=AHC=90∘.
Vậy AH⊥BCAH⊥BC.
c) Vi ΔAHB=ΔAHCΔAHB=ΔAHC (cmt) suy ra HAB^=HAC^=45∘HAB=HAC=45∘;
HCA^=HBA^=180∘−BAC^2=45∘HCA=HBA=2180∘−BAC=45∘ (cặp góc tương ứng).
Xét ΔEBAΔEBA và ΔBFCΔBFC có:
AB=CFAB=CF (gt);
BAE^=BCF^BAE=BCF (cùng bù với HAB^=HCA^=45∘HAB=HCA=45∘);
EA=BCEA=BC (gt);
Suy ra ΔEBA=ΔBFCΔEBA=ΔBFC (c.g.c).
Vậy BE=BFBE=BF (cặp cạnh tương ứng).
1) Số tiền bác Mai phải trả khi mua 55 chai dung dịch sát khuẩn là:
5.80000=4000005.80000=400000 (đồng)
Số tiền bác Mai phải trả khi mua 33 hộp khẩu trang là: 3.x3.x (đồng)
Đa thức F(x)F(x) biểu thị tổng số tiền bác Mai phải thanh toán là: 400000+3x400000+3x (đồng)
2)
a) Ta có: A(x)=2x2−3x+5+4x−2x2=(2x2−2x2)+(−3x+4x)+5=x+5A(x)=2x2−3x+5+4x−2x2=(2x2−2x2)+(−3x+4x)+5=x+5
Bậc: 11; hệ số cao nhất: 11; hệ số tự do: 55.
b) Ta có: C(x)=(x−1).A(x)+B(x)=(x−1)(x+5)+(x2−2x+5)=x2+4x−5+x2−2x+5C(x)=(x−1).A(x)+B(x)=(x−1)(x+5)+(x2−2x+5)=x2+4x−5+x2−2x+5 =(x2+x2)+(4x−2x)+(−5+5)=2x2+2x=(x2+x2)+(4x−2x)+(−5+5)=2x2+2x.