Lữ Đức Anh
Giới thiệu về bản thân



































One natural disaster that often happens in Vietnam is flooding. Due to its long coastline and tropical monsoon climate, Vietnam frequently experiences heavy rains and typhoons, especially from June to November. These floods can cause serious damage to homes, crops, and roads, particularly in central and southern regions. Many people lose their belongings, and some even lose their lives. Every year, the government and local communities work together to prepare for the rainy season by strengthening flood defenses and raising awareness. Despite these efforts, flooding remains a major challenge for the country.
Question 1:
He asked the villagers how often earthquakes occurred in that region.
Question 2:
They told me that I could find a wide range of beauty products in their store.
1. I think robots can't replace the role of teachers in education
2. People will still send letters to each other in 2050
pt đã cho \(\Leftrightarrow \frac{2 x - 50}{50} - 1 + \frac{2 x - 51}{49} - 1 + \frac{2 x - 52}{48} - 1 + \frac{2 x - 53}{47} - 1 + \frac{2 x - 200}{25} + 4 = 0\)
\(\Leftrightarrow \frac{2 x - 50 - 50}{50} + \frac{2 x - 51 - 49}{49} + \frac{2 x - 52 - 48}{48} + \frac{2 x - 53 - 47}{47} + \frac{2 x - 200 + 100}{25} = 0\)
\(\Leftrightarrow \frac{2 x - 100}{50} + \frac{2 x - 100}{49} + \frac{2 x - 100}{48} + \frac{2 x - 100}{47} + \frac{2 x - 100}{25} = 0\)
\(\Leftrightarrow \left(\right. 2 x - 100 \left.\right) \left(\right. \frac{1}{50} + \frac{1}{49} + \frac{1}{48} + \frac{1}{47} + \frac{1}{25} \left.\right) = 0\)
\(\Leftrightarrow 2 x - 100 = 0\) (vì \(\frac{1}{50} + \frac{1}{49} + \frac{1}{48} + \frac{1}{47} + \frac{1}{25} > 0\))
\(\Leftrightarrow x = 50\)
Vậy pt đã cho có tập nghiệm \(S={\left\lbrace50\right\rbrace\left.\right.}\)
Do AB // DE (gt)
Theo hệ quả của định lý Thalès, ta có:
AB/DE = BC/CD
x = BC = AB.CD : DE
x = BC = 5.7,2 : 15 = 2,4
Do AB // DE (gt)
Theo hệ quả của định lý Thalès, ta có:
AB/DE = AC/CE
y = CE = AC.DE : AB
= 3.15 : 7,2
= 6,25
=> (x+1) . 5 = (2x + 5) . 3
5x + 5 = 6x + 15
5x + 6x = 15-5
11x =10
x = 10/11
câu a,
\(\left(\right. \frac{2 x}{3 x + 1} - 1 \left.\right) : \left(\right. 1 - \frac{8 x^{2}}{9 x^{2} - 1} \left.\right) = \left(\right. \frac{2 x}{3 x + 1} - \frac{3 x + 1}{3 x + 1} \left.\right) : \left(\right. \frac{9 x^{2} - 1}{9 x^{2} - 1} - \frac{8 x^{2}}{9 x^{2} - 1} \left.\right) = \left(\right. \frac{2 x}{3 x + 1} - \frac{3 x + 1}{3 x + 1} \left.\right) : \left(\right. \frac{9 x^{2} - 1}{\left(\right. 3 x - 1 \left.\right) \left(\right. 3 x + 1 \left.\right)} - \frac{8 x^{2}}{\left(\right. 3 x - 1 \left.\right) \left(\right. 3 x + 1 \left.\right)} \left.\right) = \left(\right. \frac{2 x - 3 x - 1}{3 x + 1} \left.\right) : \left(\right. \frac{9 x^{2} - 1 - 8 x^{2}}{\left(\right. 3 x - 1 \left.\right) \left(\right. 3 x + 1 \left.\right)} \left.\right)\)
\(= \left(\right. \frac{- x - 1}{3 x + 1} \left.\right) : \left(\right. \frac{x^{2} - 1}{\left(\right. 3 x - 1 \left.\right) \left(\right. 3 x + 1 \left.\right)} \left.\right) = \frac{- x - 1}{3 x + 1} \cdot \frac{\left(\right. 3 x - 1 \left.\right) \left(\right. 3 x + 1 \left.\right)}{x^{2} - 1}\)
\(= \frac{- \left(\right. x + 1 \left.\right) \cdot \left(\right. 3 x - 1 \left.\right) \cdot \left(\right. 3 x + 1 \left.\right)}{\left(\right. 3 x + 1 \left.\right) \cdot \left(\right. x - 1 \left.\right) \cdot \left(\right. x + 1 \left.\right)} = \frac{- 3 x + 1}{x - 1}\)
câu b,
thay \(x = 2\) vào P ta được
\(\frac{- 3 \cdot 2 + 1}{2 - 1} = \frac{- 6 + 1}{1} = - 5\)
vậy \(P = 5\) khi \(x = 2\)
câu a)
\(\frac{2 y - 1}{y}-\frac{2 x + 1}{x}=\frac{2 x y - x}{x y}-\frac{2 x y + y}{x y}=\frac{2 x y - x - 2 x y - y}{x y}=\frac{- x - y}{x y}.\)
câu b)
\(\frac{2 x}{3} : \frac{5}{6 x^{2}} = \frac{2 x}{3} \cdot \frac{6 x^{2}}{5} = \frac{2 x \cdot 6 x^{2}}{3 \cdot 5} = \frac{12 x^{3}}{15} = \frac{4 x^{3}}{5}\).
Sự thiếu hiểu biết về kiến thức pháp luật là nguyên nhân chính khiến hành vi sử dụng các ấn phẩm số không quan tâm đến vấn đề bản quyền.
Yếu tố phụ góp phần là nguyên nhân của hành vi như tăng tính tò mò cho người đọc khi muốn thu hút mọi người tập trung theo dõi một sự kiện nào đó,…
Một số tác hại phổ biến như: lầm tưởng tính sự thật của sản phẩm,…
Ví dụ, sử dụng hình ảnh có bản quyền nhưng trả phí hoặc chưa xin phép tác giả.
Câu 1:
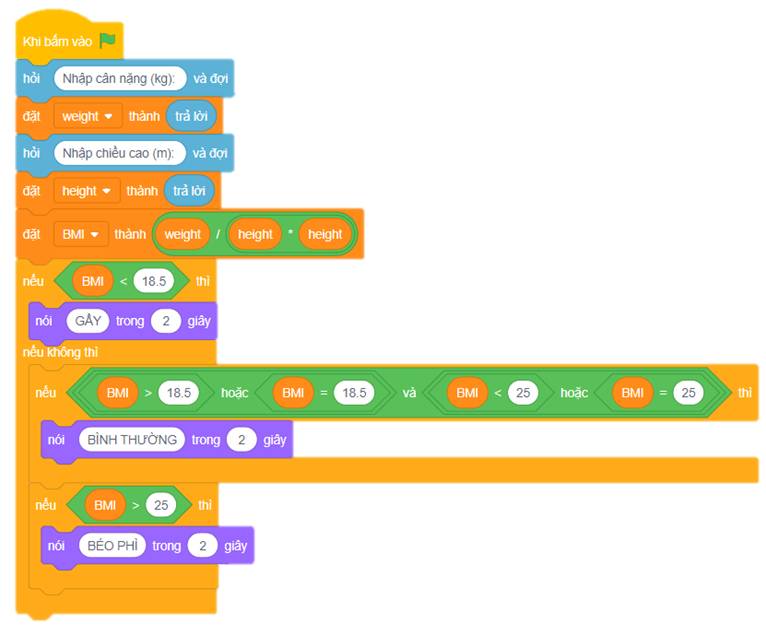
a. Mô tả chương trình dưới dạng kịch bản bằng sơ đồ hoặc bước thuật toán.
Bước 1. Nhập cân nặng. Gán giá trị nhập vào biến weight.
Bước 2. Nhập chiều cao. Gán giá trị nhập vào biến height.
Bước 3. Tính chỉ số theo công thức BMI. Gán giá trị cho biến BMI.
Bước 4. Nếu BMI < 18.5 thì hiển thị “GẦY”. Ngược lại thực hiện bước 5.
Bước 5. Nếu BMI ≥ 18.5 và BMI ≤ 25 thì hiển thị “BÌNH THƯỜNG”. Ngược lại thực hiện bước 6.
Bước 6. Nếu BMI > 25 thì hiển thị “BÉO PHÌ”.
Bước 7. Kết thúc chương trình.
b,