a) Gọi $I$ là trung điểm $HC$.

$HF\perp AC$ (gt) suy ra HFC^=90∘HFC=90∘

Xét tam giác $HFC$ vuông tại $F$, $FI$ là trung tuyến ứng với cạnh huyền nên FI=HI=CI=12HCFI=HI=CI=21​HC (1)

$HE\perp BC$ (gt) suy ra HEC^=90∘HEC=90∘

Xét tam giác $HEC$ vuông tại $E$, $EI$ là trung tuyến ứng với cạnh huyền nên EI=HI=CI=12HCEI=HI=CI=21​HC (2)

gọi chiều rộng của mảnh vườn là x (m)              (đk :x>0)

Khi đó chiều dài của mảnh vườn  là : 3x (m)

Vì người ta làm 1 lối đi xung quanh vườn và có diện tích đất để trồng trọt là 4329m² nên ta có pt 

(x-3).(3x-3)=4329

3x²-3x-9x+9=4329

3x²-12x-4320=0

X²-4x-1440=0

Δ=(-4)²-4.(-1440)=5776>0 nên tao có 2 nghiệm phân biệt là:

X=(4+76)/2=40 (tm)                                      x=(4-76)/2=-36(ktm)

Vậy chiều rộng mảnh vườn là 40m , chiều dài mảnh vườn là 120m

Gọi chiều rộng mảnh đất là $x$ (m) (ĐK: $x>0$)

$\Rightarrow$ Chiều dài mảnh đất là $x+7$ (m).

Vì độ dài đường chéo của mảnh đất hình chữ nhật là $13$ m nên ta có phương trình:

x2+(x+7)2=132x²+(x+7)²=13²
 

x2+x2+14x+49=169x
²+x²
+14x+49=169

2x2+14x−120=02x²
+14x−120=0

x2+7x−60=0x
²+7x−60=0

Δ=7²-4*(-60)=289>0 nên pt có 2 nghiệm phân biệt là :
Δ=72−4.(−60)=289=

x=−7+172=5x=
​(-7+17)/2=5 (tm); x=−7−172=−12x=

​(-7-17)/2=−12 (ktm)

$\Rightarrow$ Chiều rộng của mảnh đất là $5$ m, chiều dài của mảnh đất là $5+7=12$ m.

Vậy diện tích mảnh đất hình chữ nhật là $S=5.12=60$ (m22).

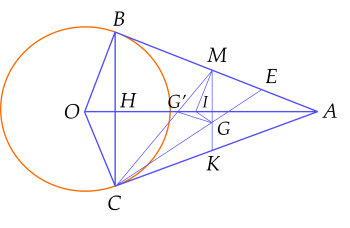
a) Do $AB,AC$ là hai tiếp tuyến cắt nhau của đường tròn $(O)$ nên ABO^=ACO^=90∘ABO=ACO=90∘.

Gọi $I$ là trung điểm $OA$.

Xét tam giác $OAB$ vuông tại $B$ có $BI$ là trung tuyến ứng với cạnh huyền nên IB=IA=IO=12AOIB=IA=IO=21​AO (1)

Xét tam giác $OAC$ vuông tại $C$ có $CI$ là trung tuyến ứng với cạnh huyền nên IC =IA=IO=12AOIC =IA=IO=21​AO (2)

Từ (1) và (2) suy ra $IB=IC=IA=IO$.

Suy ra $B,C$ thuộc đường tròn tâm $I$ đường kính $OA$.

b) Ta có AM.AO=AB2.2AI=AB.AIAM.AO=2AB​.2AI=AB.AI.

c) Gọi $E$ là trung điểm $MA$, do $G$ là trọng tâm $\Delta CMA$ nên $G\in CE$ và GECE=13CEGE​=31​.

Mặt khác MEBE=13BEME​=31​ $($vì ME=MA2=MB2ME=2MA​=2MB​ nên ME=BE3)ME=3BE​)

Suy ra GECE=MEBECEGE​=BEME​, theo định lí Thalès đảo ta có:

$MG$ // $BC$.

d) Gọi G′G′ là giao điểm của $OA$ và $CM$ suy ra G′G′ là trọng tâm $\Delta ABC$.

Nên G′MCM=13=GECE′CMG′M​=31​=CE′GE​

Theo định lý Thalès đảo ta có GG′GG′ // $ME$ (1)

$MI$ là đường trung bình trong $\Delta OAB$ suy ra $MI$ // $OB$, mà $AB\perp OB$ (cmt) nên $MI\perp AB$, nghĩa là $MI\perp ME$ (2).

Từ (1) và (2) suy ra MI⊥GG′MI⊥GG′,

Lại có GI′⊥MKGI′⊥MK (vì $OA\perp MK$) nên $I$ là trực tâm ΔMGG′ΔMGG′

Suy ra GI⊥G′MGI⊥G′M tức là $GI\perp CM$.

a) Tứ giác $BCED$ nội tiếp, $C$ thuộc đường tròn đường kính $AB$ suy ra \widehat{ACB}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Suy ra ECB^=90∘ECB=90∘.

Mặt khác $ED\perp AB$ tại $D$ (gt) suy ra EDB^=90∘EDB=90∘.

Gọi $I$ là trung điểm của $BE$.

Xét tam giác $BCE$ có BCE^=90∘BCE=90∘ và $CI$ là đường trung tuyến ứng với cạnh huyền nên IC=IE=IB=12BEIC=IE=IB=21​BE.

Xét tam giác $BED$ có BDE^=90∘BDE=90∘ và $DI$ là đường trung tuyến ứng với cạnh huyền nên ID=IE=IB=12BEID=IE=IB=21​BE.

Suy ra $BCED$ là tứ giác nội tiếp đường tròn tâm $I$, đường kính $BE$.

b) Xét $\Delta AED$ và $\Delta ABC$ có:

BAC^BAC chung

ADE^=ACB^=90∘ADE=ACB=90∘

Suy ra $\Delta AED\backsim \Delta ABC$ (g.g)

Suy ra AEAB=ADACABAE​=ACAD​ (cặp cạnh tương ứng tỉ lệ) hay $AC.AE=AD.AB$.

Mà $D$ là trung điểm của $AO$ (gt) suy ra AD=12AOAD=21​AO

$O$ là tâm đường tròn đường kính $AB$ (gt) nên AO=12ABAO=21​AB

Suy ra AD=12AO=12.12AB=14ABAD=21​AO=21​.21​AB=41​AB

Do đó, AC.AE=14AB.AB=AB24AC.AE=41​AB.AB=4AB2​ (đpcm)

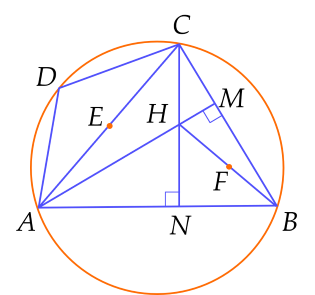
a) Chứng minh ABC^=CHM^ABC=CHM.

Vì $AM,CN$ là các đường cao của $\Delta ABC$ nên $AM\perp BC$ và $CN\perp AB$

Suy ra BMH^=BNH^=90∘BMH=BNH=90∘.

Gọi $F$ là trung điểm của $HB$.

Xét tam giác $HNB$ có HNB^=90∘HNB=90∘ và $NF$ là đường trung tuyến ứng với cạnh huyền nên FN=FH=FB=12BHFN=FH=FB=21​BH (1)

Xét tam giác $HMB$ có HMB^=90∘HMB=90∘ và $MF$ là đường trung tuyến ứng với cạnh huyền nên FM=FH=FB=12BHFM=FH=FB=21​BH (2)

Suy ra $BNHM$ là tứ giác nội tiếp đường tròn tâm $F$, đường kính $HB$.

Do đó MBN^+NHM^=180∘MBN+NHM=180∘ (tổng hai góc đối bằng 180∘180∘.

hay CBA^+NHM^=180∘CBA+NHM=180∘.

Mà MBN^+NHM^=180∘MBN+NHM=180∘ (hai góc kề bù) do đó CBA^=MBN^CBA=MBN.

b) Chứng minh ADC^=AHC^ADC=AHC.

Tứ giác $BNHM$ nội tiếp nên MBN^+NHM^=180∘MBN+NHM=180∘

Mà AHC^=NHM^AHC=NHM (đối đỉnh) nên MBN^+AHC^=180∘MBN+AHC=180∘ hay ABC^+AHC^=180∘ABC+AHC=180∘

Mặt khác tứ giác $BNHM$ nội tiếp đường tròn tâm $(O)$ nên ADC^+ABC^=180∘ADC+ABC=180∘.

Do đó ADC^=AHC^ADC=AHC.

c) Chứng minh MAC^=MNC^MAC=MNC.

Ta chứng minh $ACMN$ là tứ giác nội tiếp.

Gọi $E$ là trung điểm $AC$.

Xét tam giác $AMC$ có AMC^=90∘AMC=90∘ và $ME$ là đường trung tuyến nên EM=EC=EA=12ACEM=EC=EA=21​AC (3) 

Xét tam giác $ANC$ có ANC^=90∘ANC=90∘ và $NE$ là đường trung tuyến nên EN=EC=EA=12ACEN=EC=EA=21​AC (4)

Từ (3) và (4) suy ra $EM=EN=EC=EA$.

Vậy tứ giác $ACMN$ nội tiếp được đường tròn có tâm $E$ đường kính $AC$.

Suy ra MAC^=MNC^MAC=MNC (hai góc nội tiếp cùng chắn cung $MC$ của đường tròn tâm $E$).

d) Chứng minh MAC^+90∘=ANM^MAC+90∘=ANM.

Ta có MAC^+ACM^=90∘MAC+ACM=90∘ (hai góc phụ nhau)

Hay ACM^=90∘−MAC^ACM=90∘−MAC

Mà ACM^+ANM^=180∘ACM+ANM=180∘ (tứ giác $ACMN$ nội tiếp được đường tròn) nên 90∘−MAC^+ANM^=180∘90∘−MAC+ANM=180∘

Suy ra MAC^+90∘=ANM^MAC+90∘=ANM.

) Chứng minh tứ giác $BFHD$ nội tiếp.

Xét đường tròn $(I)$ có CFB^=90∘CFB=90∘ (góc nội tiếp chắn nửa đường tròn)

Suy ra $CF\perp AB$.

CFB^=90∘CFB=90∘ (góc nội tiếp chắn nửa đường tròn)

Suy ra $BE\perp AC$

Mà $CF$ cắt $BE$ tại $H$ nên $H$ là trực tâm của tam giác $ABC$

Hay $AH\perp BC$, suy ra HDB^=90∘HDB=90∘

Gọi $K$ là trung điểm $BH$.

Xét tam giác $HDB$ có HDB^=90∘HDB=90∘ và $DK$ là đường trung tuyến ứng với cạnh huyền nên KD=KH=KB=12BHKD=KH=KB=21​BH (1)

Xét tam giác $HFB$ có HFB^=90∘HFB=90∘ và $EK$ là đường trung tuyến ứng với cạnh huyền nên KE=KH=KB=12HBKE=KH=KB=21​HB (2)

Từ (1) và (2) suy ra $KB=KH=KF=KD$.

Vậy tứ giác $BFHD$ nội tiếp được đường tròn có tâm $K$ đường kính $BH$.

b) Chứng minh tứ giác $ABDE$ nội tiếp.

Gọi $O$ là trung điểm $AB$.

Xét tam giác $ADB$ có ADB^=90∘ADB=90∘ và $DO$ là đường trung tuyến ứng với cạnh huyền nên OD=OA=OB=12ABOD=OA=OB=21​AB (3)

Xét tam giác $AEB$ có AEB^=90∘AEB=90∘ và $EO$ là đường trung tuyến ứng với cạnh huyền nên OE=OA=OB=12ABOE=OA=OB=21​AB (4)

Từ (3) và (4) suy ra $OD=OE=OA=OB$.

Vậy tứ giác $ABDE$ nội tiếp được đường tròn có tâm $O$ đường kính $AB$.

gọi O là trung điểm của BC

xét tam giác BEC vuông tại E , EO là trung tuyến ứng với cạnh huyền BC nên 

EO = BC/2 suy ra B,E,C thuộc đường tròn (O) đường kính BC            (1)

+) xét tam giác BDC vuông tại D , DO là trung tuyến ứng cạnh huyền BC nên

DO = BC/2 suy ra B,D,C thuộc đường tròn (O) đường kính BC               (2)

+) Từ 1 và 2 suy ra B,E,D,C thuộc đường tròn (o) đường kính BC 

Suy ra BCDE là tứ giác nội tiếp

b,

Gọi i là trung điểm của AH

+) xét tam giác ADH vuông tại D , DI là trung tuyến ứng cạnh huyền AH nên

DI = AH/2 suy ra A,D,H thuộc đường tròn (i) đường kính AH                (3)

+) xét tam giác AEH vuông tại E , EI là trung tuyến ứng cạnh huyền AH nên

EI = AH/2 suy ra A,E,H thuộc đường tròn (i) đường kính AH                 (4)

+) Từ 1 và 2 suy ra A,E,H,D thuộc đường tròn (i) đường kính AH

Suy ra ADHE là tứ giác nội tiếp