Tiêu dùng thông mình là vc biết chị Tiêu có kế hoạch ,tiết kiệm ,hậu quả phù hợp với đặt điểm của bản thân

a) Dấu hiệu và hành vi vi phạm pháp luật của anh T: -Dấu hiệu vi phạm pháp luật: Anh T điều khiển xe mô tô đi ngược chiều trên đường cao tốc, vi phạm quy định về giao thông. -Hành vi vi phạm: Anh T không tuân thủ quy định về làn đường, gây nguy hiểm cho bản thân và người tham gia giao thông khác

. b) Trách nhiệm pháp lý của anh T: -Anh T bị phạt tiền và tước quyền sử dụng Giấy phép lái xe 3 tháng theo quy định của pháp luật về giao thông đường bộ.

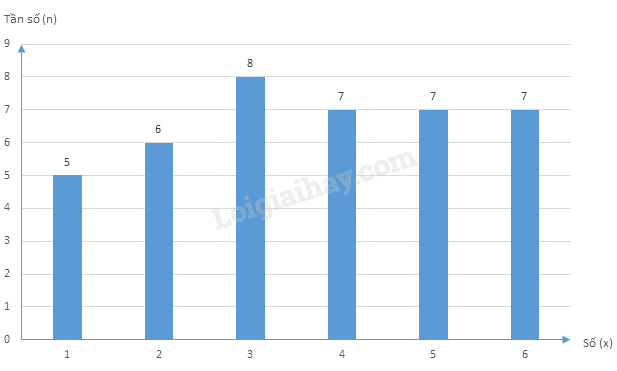
Có 6 giá trị khác nhau là: 1, 2, 3, 4, 5, 6.

b)   n1=5,n2=6,n3=8,n4=7,n5=7,n6=7n1=5,n2=6,n3=8,n4=7,n5=7,n6=7

Biểu đồ cột:

c)      f1=12,5%,f2=15%,f3=20%,f4=17,5%,f5=17,5%,f6=17,5%f1=12,5%,f2=15%,f3=20%,f4=17,5%,f5=17,5%,f6=17,5%

Cỡ mẫu là: 24 + 26 + 6 + 4 = 50 Tần số tương đối của 24 là 24 50 .100 % = 48 % Tần số tương đối của 16 là 16 50 .100 % = 32 % Tần số tương đối của 6 là 6 50 .100 % = 12 % Tần số tương đối của 4 là 4 50 .100 % = 8 % Vậy số liệu sai ở đây là tần số tương đối của 6 phải là 12%.

Xác định cỡ mẫu bằng cách lấy cột dọc nhân cột ngang,

-  Lập bảng tần số theo: Bảng tần số biểu diễn tần số của mỗi giá trị trong mẫu dữ liệu gồm hai dòng, dòng trên ghi các giá trị khác nhau của mẫu dữ liệu, dòng dưới ghi các tần số tương ứng với mỗi giá trị đó.

-  Tần số tương đối của một giá trị x trong mẫu dữ liệu được tính theo công thức f=mN.100%f=mN.100%, trong đó m là tần số của x và N là cỡ mẫu.

-  Vẽ biểu đồ tần số tương đối dạng hình quạt tròn:  hình quạt tròn biểu thị tần số tương đối a% có số đo cung tương ứng a% . 360^o = 3,6a^o

Xác định cỡ mẫu bằng cách lấy cột dọc nhân cột ngang, - Lập bảng tần số theo: Bảng tần số biểu diễn tần số của mỗi giá trị trong mẫu dữ liệu gồm hai dòng, dòng trên ghi các giá trị khác nhau của mẫu dữ liệu, dòng dưới ghi các tần số tương ứng với mỗi giá trị đó. - Tần số tương đối của một giá trị x trong mẫu dữ liệu được tính theo công thức f = m N .100 % , trong đó m là tần số của x và N là cỡ mẫu. - Biểu đồ tần số tương đối ghép nhóm dạng cột gồm các cột kề nhau, mỗi cột tương ứng với một nhóm. Cột biểu diễn nhóm [a;b) có đầu mút trái là a, đầu mút phải là b và có chiều cao tương ứng với tần số tương đối của nhóm. -

a: Xét (O) có

 

ΔACB nội tiếp

 

AB là đường kính

 

Do đó: ΔACB vuông tại C

 

Xét tứ giác BCED có 

B

C

E

^

+

B

D

E

^

=

9

0

0

+

9

0

0

=

18

0

0

BCE

 + 

BDE

 =90 

0

 +90 

0

 =180 

0

Do tam giác ABC có hai đường cao AM, CN nên 

ˆ

H

M

B

=

90

∘

,

ˆ

B

N

H

=

90

∘

 

Xét tứ giác HMBN có:

 

ˆ

N

H

M

+

ˆ

H

M

B

+

ˆ

M

B

N

+

ˆ

B

N

H

=

360

∘

ˆ

N

H

M

+

ˆ

M

B

N

=

360

∘

−

ˆ

H

M

B

−

ˆ

B

N

H

ˆ

N

H

M

+

ˆ

M

B

N

=

360

∘

−

90

∘

−

90

∘

=

180

∘

.

 

Hay 

ˆ

M

H

N

+

ˆ

A

B

C

=

180

∘

.

 

b) Vì ABCD nội tiếp đường tròn nên  

ˆ

C

D

A

+

ˆ

A

B

C

=

180

∘

.

 

mà 

ˆ

M

H

N

+

ˆ

A

B

C

=

180

∘

 (câu a)

 

suy ra 

ˆ

C

D

A

=

ˆ

M

H

N

, hơn nữa 

ˆ

C

H

A

=

ˆ

M

H

N

 (đối đỉnh)

 

vậy 

ˆ

C

H

A

=

ˆ

C

D

A

.

 

c) Xét tam giác AMB vuông tại M có:

ˆ

B

A

M

+

ˆ

A

M

B

=

ˆ

B

A

M

+

90

∘

=

180

∘

−

ˆ

M

B

A

.

 

Mà 

180

∘

−

ˆ

M

B

A

=

ˆ

A

D

C

 (do ABCD nội tiếp)

 

Vậy 

ˆ

A

D

C

=

ˆ

B

A

M

+

90

∘

.

a: Xét tứ giác ABOC có 

O

B

A

^

+

O

C

A

^

=

9

0

0

+

9

0

0

=

18

0

0

OBA

 + 

OCA

 =90 

0

 +90 

0

 =180 

0

 

 

nên ABOC là tứ giác nội tiếp đường tròn đường kính AO

 

Tâm I là trung điểm của AO

 

b: Xét ΔABO có I,M lần lượt là trung điểm của AO,AB

 

=>MI là đường trung bình của ΔABO

 

=>MI//BO

 

Xét ΔAMI và ΔABO có 

A

M

A

B

=

A

I

A

O

(

=

1

2

)

AB

AM

​

 = 

AO

AI

​

 (= 

2

1

​

 ) và góc MAI chung

 

nên ΔAMI~ΔABO

 

=>

A

M

A

B

=

A

I

A

O

AB

AM

​

 = 

AO

AI

​

 

 

=>

A

M

⋅

A

O

=

A

B

⋅

A

I

AM⋅AO=AB⋅AI

 

c: Gọi H là trung điểm của AM

 

Xét ΔCMA có

 

G là trọng tâm

 

H là trung điểm của AM

 

Do đó: C,G,H thẳng hàng và 

C

G

=

2

3

C

H

CG= 

3

2

​

 CH

 

Ta có: CG+GH=CH

 

=>

G

H

=

H

C

−

2

3

H

C

=

1

3

H

C

GH=HC− 

3

2

​

 HC= 

3

1

​

 HC

 

Ta có: H là trung điểm của AM

 

=>

H

A

=

H

M

=

A

M

2

=

B

M

2

HA=HM= 

2

AM

​

 = 

2

BM

​

 

 

Ta có: HM+MB=HB

 

=>

H

B

=

1

2

M

B

+

M

B

=

3

2

M

B

HB= 

2

1

​

 MB+MB= 

2

3

​

 MB

 

=>

H

M

H

B

=

1

2

M

A

3

2

M

A

=

1

3

HB

HM

​

 = 

2

3

​

 MA

2

1

​

 MA

​

 = 

3

1

​

 

 

Xét ΔHCB có 

H

M

H

B

=

H

G

H

C

(

=

1

3

)

HB

HM

​

 = 

HC

HG

​

 (= 

3

1

​

 )

 

nên MG//BC

a: Xét (I) có

 

ΔBFC nội tiếp

 

BC là đường kính

 

Do đó: ΔBFC vuông tại F

 

=>CF

⊥

⊥AB tại F

 

Xét (I) có

 

ΔBEC nội tiếp

 

BC là đường kính

 

Do đó: ΔBEC vuông tại E

 

=>BE

⊥

⊥AC tại E

 

Xét ΔABC có

 

CF,BE là các đường cao

 

CF cắt BE tại H

 

Do đó: H là trực tâm của ΔABC

 

=>AH

⊥

⊥BC tại D

 

Xét tứ giác BFHD có 

B

F

H

^

+

B

D

H

^

=

9

0

0

+

9

0

0

=

18

0

0

BFH

 + 

BDH

 =90 

0

 +90 

0

 =180 

0

 

 

nên BFHD là tứ giác nội tiếp

 

b: Xét tứ giác ABDE có 

A

E

B

^

=

A

D

B

^

=

9

0

0

AEB

 = 

ADB

 =90 

0

 

 

nên ABDE là tứ giác nội tiếp