

Nguyễn Đức Long
Giới thiệu về bản thân



































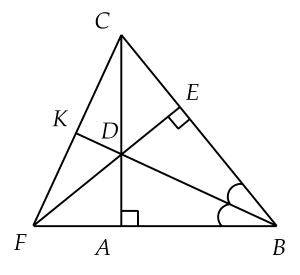
GT | \(\Delta A B C : A = 9 0^{\circ}\) \(B D\) là phân giác của góc \(B\) \(D E \bot B C \left(\right. E \in A C \left.\right)\) \(B A \cap E D = \left{\right. F \left.\right}\) \(B D \cap F C = \left{\right. K \left.\right}\) |
KL | a) \(\Delta B A D = \Delta B E D\). b) \(\Delta B C F\) cân tại \(B\). c) \(B D\) là đường trung tuyesn của \(\Delta B C F\). |
a) Xét \(\Delta B A D\) và \(\Delta B E D\) lần lượt vuông tại \(A\) và \(E\).
\(B D\) chung.
\(\hat{A B D} = \hat{E B D}\) (\(B D\) là tia phân giác).
Suy ra \(\Delta B A D = \Delta B E D\) (cạnh huyền - góc nhọn).
b) Vì \(\Delta B A D = \Delta B E D \left(\right. c / m\) phần a) nên \(A D = E D ; B A = B E\) (2)
Xét \(\Delta A F D\) vuông tại \(A\) và \(\Delta E C D\) vuông tại \(E\) có:
\(A D = E D \left(\right. c m t \left.\right)\)
\(\hat{A D F} = \hat{E D C}\) (đối đỉnh)
Suy ra \(\Delta A F D = \Delta E C D\) (cạnh góc vuông - góc nhọn)
Nên \(A F = E C\) (2).
Từ (1) và (2) suy ra \(A F + B A = B E + E C\)
Hay \(B F = B C\)
Vậy \(\Delta B C F\) cân tại \(B\).
c) Giả sử \(B D\) kéo dài cắt \(F C\) tại \(K\)
Xét \(\Delta B K F\) và \(\Delta B K C\) có:
\(B K\) là cạnh chung
\(\hat{K B F} = \hat{K B C}\) (Vì \(B D\) là phân giác của \(\hat{A B C}\) )
\(B F = B C\) ( chứng minh phần \(b \left.\right)\)
Suy ra \(\Delta B K F = \Delta B K C \left(\right.\) c.g.c \(\left.\right)\)
Suy ra \(K F = K C\) (hai cạnh tương ứng)
Vậy \(B K\) hay \(B D\) là đường trung tuyến của \(\Delta B C F\).
GT | \(\Delta A B C : A = 9 0^{\circ}\) \(B D\) là phân giác của góc \(B\) \(D E \bot B C \left(\right. E \in A C \left.\right)\) |
KL | a) \(\Delta B A D = \Delta B E D\). b) \(\Delta B C F\) cân tại \(B\). c) \(B D\) là đường trung tuyesn của \(\Delta B C F\). |

a) Xét \(\Delta B A D\) và \(\Delta B E D\) lần lượt vuông tại \(A\) và \(E\).
\(B D\) chung.
\(\hat{A B D} = \hat{E B D}\) (\(B D\) là tia phân giác).
Suy ra \(\Delta B A D = \Delta B E D\) (cạnh huyền - góc nhọn).
b) Vì \(\Delta B A D = \Delta B E D \left(\right. c / m\) phần a) nên \(A D = E D ; B A = B E\) (2)
Xét \(\Delta A F D\) vuông tại \(A\) và \(\Delta E C D\) vuông tại \(E\) có:
\(A D = E D \left(\right. c m t \left.\right)\)
\(\hat{A D F} = \hat{E D C}\) (đối đỉnh)
Suy ra \(\Delta A F D = \Delta E C D\) (cạnh góc vuông - góc nhọn)
Nên \(A F = E C\) (2).
Từ (1) và (2) suy ra \(A F + B A = B E + E C\)
Hay \(B F = B C\)
Vậy \(\Delta B C F\) cân tại \(B\).
c) Giả sử \(B D\) kéo dài cắt \(F C\) tại \(K\)
Xét \(\Delta B K F\) và \(\Delta B K C\) có:
\(B K\) là cạnh chung
\(\hat{K B F} = \hat{K B C}\) (Vì \(B D\) là phân giác của \(\hat{A B C}\) )
\(B F = B C\) ( chứng minh phần \(b \left.\right)\)
Suy ra \(\Delta B K F = \Delta B K C \left(\right.\) c.g.c \(\left.\right)\)
Suy ra \(K F = K C\) (hai cạnh tương ứng)
Vậy \(B K\) hay \(B D\) là đường trung tuyến của \(\Delta B C F\).
GT | \(\Delta A B C : A = 9 0^{\circ}\) \(B D\) là phân giác của góc \(B\) \(D E \bot B C \left(\right. E \in A C \left.\right)\) \(B A \cap E D = \left{\right. F \left.\right}\) \(B D \cap F C = \left{\right. K \left.\right}\) |
KL | a) \(\Delta B A D = \Delta B E D\). b) \(\Delta B C F\) cân tại \(B\). c) \(B D\) là đường trung tuyesn của \(\Delta B C F\). |

a) Xét \(\Delta B A D\) và \(\Delta B E D\) lần lượt vuông tại \(A\) và \(E\).
\(B D\) chung.
\(\hat{A B D} = \hat{E B D}\) (\(B D\) là tia phân giác).
Suy ra \(\Delta B A D = \Delta B E D\) (cạnh huyền - góc nhọn).
b) Vì \(\Delta B A D = \Delta B E D \left(\right. c / m\) phần a) nên \(A D = E D ; B A = B E\) (2)
Xét \(\Delta A F D\) vuông tại \(A\) và \(\Delta E C D\) vuông tại \(E\) có:
\(A D = E D \left(\right. c m t \left.\right)\)
\(\hat{A D F} = \hat{E D C}\) (đối đỉnh)
Suy ra \(\Delta A F D = \Delta E C D\) (cạnh góc vuông - góc nhọn)
Nên \(A F = E C\) (2).
Từ (1) và (2) suy ra \(A F + B A = B E + E C\)
Hay \(B F = B C\)
Vậy \(\Delta B C F\) cân tại \(B\).
c) Giả sử \(B D\) kéo dài cắt \(F C\) tại \(K\)
Xét \(\Delta B K F\) và \(\Delta B K C\) có:
\(B K\) là cạnh chung
\(\hat{K B F} = \hat{K B C}\) (Vì \(B D\) là phân giác của \(\hat{A B C}\) )
\(B F = B C\) ( chứng minh phần \(b \left.\right)\)
Suy ra \(\Delta B K F = \Delta B K C \left(\right.\) c.g.c \(\left.\right)\)
Suy ra \(K F = K C\) (hai cạnh tương ứng)
Vậy \(B K\) hay \(B D\) là đường trung tuyến của \(\Delta B C F\).
GT | \(\Delta A B C : A = 9 0^{\circ}\) \(B D\) là phân giác của góc \(B\) \(D E \bot B C \left(\right. E \in A C \left.\right)\) \(B A \cap E D = \left{\right. F \left.\right}\) \(B D \cap F C = \left{\right. K \left.\right}\) |
KL | a) \(\Delta B A D = \Delta B E D\). b) \(\Delta B C F\) cân tại \(B\). c) \(B D\) là đường trung tuyesn của \(\Delta B C F\). |

a) Xét \(\Delta B A D\) và \(\Delta B E D\) lần lượt vuông tại \(A\) và \(E\).
\(B D\) chung.
\(\hat{A B D} = \hat{E B D}\) (\(B D\) là tia phân giác).
Suy ra \(\Delta B A D = \Delta B E D\) (cạnh huyền - góc nhọn).
b) Vì \(\Delta B A D = \Delta B E D \left(\right. c / m\) phần a) nên \(A D = E D ; B A = B E\) (2)
Xét \(\Delta A F D\) vuông tại \(A\) và \(\Delta E C D\) vuông tại \(E\) có:
\(A D = E D \left(\right. c m t \left.\right)\)
\(\hat{A D F} = \hat{E D C}\) (đối đỉnh)
Suy ra \(\Delta A F D = \Delta E C D\) (cạnh góc vuông - góc nhọn)
Nên \(A F = E C\) (2).
Từ (1) và (2) suy ra \(A F + B A = B E + E C\)
Hay \(B F = B C\)
Vậy \(\Delta B C F\) cân tại \(B\).
c) Giả sử \(B D\) kéo dài cắt \(F C\) tại \(K\)
Xét \(\Delta B K F\) và \(\Delta B K C\) có:
\(B K\) là cạnh chung
\(\hat{K B F} = \hat{K B C}\) (Vì \(B D\) là phân giác của \(\hat{A B C}\) )
\(B F = B C\) ( chứng minh phần \(b \left.\right)\)
Suy ra \(\Delta B K F = \Delta B K C \left(\right.\) c.g.c \(\left.\right)\)
Suy ra \(K F = K C\) (hai cạnh tương ứng)
Vậy \(B K\) hay \(B D\) là đường trung tuyến của \(\Delta B C F\).