

Phan Minh Nhật
Giới thiệu về bản thân



































a) Đường thẳng (d):(d):
| xx | 00 | 44 |
| y=−12x+2y=−21x+2 | 22 | 00 |
Parabol (P)(P):
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=14x2y=41x2 | 11 | 1441 | 00 | 1441 | 11 |
Vẽ đồ thị:
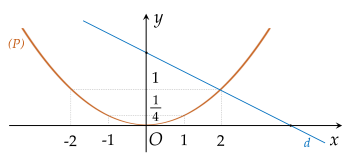
b) Tìm tọa độ giao điểm của (P)(P) và (d)(d)
Hoành độ giao điểm của (P)(P) và (d)(d) là nghiệm của phương trình
14x2=−12x+241x2=−21x+2
x2+2x−8=0x2+2x−8=0
Δ′=12−(−8)=9>0Δ′=12−(−8)=9>0
Do Δ′>0Δ′>0 nên phương trình đã cho có hai nghiệm phân biệt là x=−4x=−4 và x=2x=2
+ Với x=−4x=−4 thì y=4y=4
+ Với x=2x=2 thì y=1y=1.
Bảng giá trị hàm số y=2x2y=2x2:
| xx | −2−2 | −1−1 | 00 | 11 | 22 |
| y=2x2y=2x2 | 88 | 22 | 00 | 22 | 88 |
Đồ thị hàm số y=2x2y=2x2 là đường cong Parabol đi qua điểm OO, nhận OyOy làm trục đối xứng, bề lõm hướng lên trên.
Đồ thị hàm số y=x+1y=x+1 là đường thẳng đi qua điểm (0;1)(0;1) và (−1;0)(−1;0)
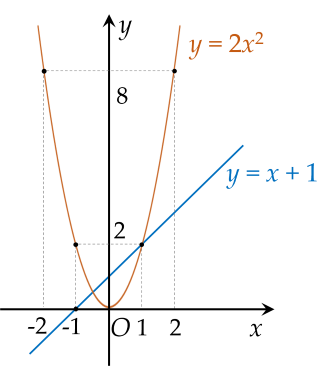
b) Tìm tọa độ giao điểm của (P)(P) và (d)(d) bằng phép tính.
Hoành độ giao điểm của (P)(P) và (d)(d) là nghiệm của phương trình
2x2=x+12x2=x+1
2x2−x−1=02x2−x−1=0.
Ta có a+b+c=2−1−1=0a+b+c=2−1−1=0 nên phương trình có hai nghiệm phân biệt x=1x=1 và x=ca=−12x=ac=−21.
+ Với x=1x=1 thì y=1+1=2y=1+1=2
+ Với x=−12x=−21 thì y=−12+1=12y=−21+1=21.
Vậy tọa độ giao điểm của (P)(P) và (d)(d) là (1;2)(1;2) và (−12;12)(−21;21).