Gọi vận tốc riêng của ca nô là \(x\) (km/h, \(x > 3\)).

Vận tốc ca nô khi đi xuôi khúc sông từ \(A\) đến \(B\) là: \(x + 3\) (km/h);

Vận tốc ca nô khi đi ngược khúc sông từ \(B\) về \(A\) là: \(x - 3\) (km/h);

Khúc sông \(A B\) có chiều dài không đổi nên ta có phương trình: \(\frac{3}{2} \left(\right. x + 3 \left.\right) = 2 \left(\right. x - 3 \left.\right)\).

Giải phương trình trên ta nhận được \(x = 21\) (thỏa mãn)

Do đó vận tốc riêng của ca nô là \(21\) km/h.

Chiều dài khúc sông là: \(2 \left(\right. 21 - 3 \left.\right) = 36\) (km).

Vậy vận tốc riêng của cano là \(21\) km/h, chiều dài khúc sông là \(36\) km .

a. Ta có: \(3 x - 4 = 5 + x\)

\(3 x - x = 5 + 4\)

\(2 x = 9\)

\(x = \frac{9}{2}\).

Vậy phương trình đã cho có nghiệm \(x = \frac{9}{2}\).

b. Ta có: \(3 \left(\right. x - 1 \left.\right) - 7 = 5 \left(\right. x + 2 \left.\right)\)

\(3 x - 3 - 7 = 5 x + 10\)

\(5 x - 3 x = - 3 - 7 - 10\)

\(2 x = - 20\)

\(x = - 10\).

Vậy phương trình có nghiệm \(x = - 10\).

a) \(\Delta A I E \sim \Delta A C I\) (g.g) suy ra \(\frac{A I}{A C} = \frac{A E}{A I}\) hay \(A I^{2} = A E . A C\) (1)

Chứng minh tương tự:

\(\Delta A I K \sim \Delta A K B\) (g.g) suy ra \(\frac{A K}{A B} = \frac{A F}{A K}\) hay \(A K^{2} = A B . A F\) (2)

Mà \(\Delta A B E \sim \Delta A C F\) (g.g) suy ra \(\frac{A B}{A C} = \frac{A E}{A F}\) hay \(A B . A F = A C . A E\) (3)

Từ (1), (2) và (3) ta có \(A I^{2} = A K^{2}\) suy ra \(A I = A K\).

b) Vì \(\hat{A} = 60^{\circ}\) suy ra \(\hat{B_{1}} = 30^{\circ}\)

Trong tam giác \(A B E\) vuông tại \(E\) nên \(A E = \frac{1}{2} A B ,\)

Trong tam giác \(A F C\) vuông tại \(F\) có \(\hat{C_{1}} = 30^{\circ}\) suy ra \(A F = \frac{1}{2} A C\).

Do đó, \(\Delta A E F \sim \Delta A B C\) (c.g.c).

suy ra \(\frac{S_{A E F}}{S_{A B C}} = \left(\left(\right. \frac{A E}{A B} \left.\right)\right)^{2} = \frac{1}{4}\).

Vậy \(S_{A E F} = \frac{1}{4} . 120 = 30\) cm\(^{2}\).

Gọi \(B F\) cắt \(D C\) tại \(K\), \(B E\) cắt \(D C\) tại \(I\), và \(E F\) cắt \(A B\) tại \(G\).

\(\Delta F A B\) có \(D K\) // \(A B\) suy ra \(\frac{D K}{A B} = \frac{F D}{F A}\) (1)

\(\Delta F A G\) có \(D H\) // \(A G\) suy ra \(\frac{D H}{A G} = \frac{F D}{F A}\) (2)

Từ (1) và (2) suy ra \(\frac{D K}{A B} = \frac{D H}{A G}\) hay \(\frac{D K}{D H} = \frac{A B}{A G}\) (*)

Tương tự \(\Delta E I C\) có \(A B\) // \(I C\) suy ra \(\frac{I C}{A B} = \frac{E C}{E A}\) (3)

\(\Delta E H C\) có \(H C\) // \(A B\) suy ra \(\frac{H C}{A G} = \frac{E C}{E A}\) (4)

Từ (3) và (4) ta có \(\frac{I C}{A B} = \frac{H C}{A G}\) hay \(\frac{I C}{H C} = \frac{A B}{A G}\) (**)

Từ (*) và (**) ta có \(\frac{D K}{D H} = \frac{I C}{H C}\).

Mà \(D H = H C\) (gt) suy ra \(D K = I C\)

Mặt khác \(B D = B C\) (gt) nên \(\Delta B D C\) cân

Suy ra \(\hat{B D K} = \hat{B C I}\)

Vậy \(\Delta B D K = \Delta B C I\) (c.g.c)

Suy ra \(\hat{D B K} = \hat{C B I}\).

a) \(\Delta A B E\) có \(A M\) // \(D G\) suy ra \(\frac{A E}{E G} = \frac{E B}{E D}\) (1)

\(\Delta A D E\) có \(A D\) // \(B K\) suy ra \(\frac{E B}{E D} = \frac{E K}{E A}\) (2)

Từ (1) và (2) ta có \(\frac{A E}{E G} = \frac{E K}{E A}\) nên \(A E^{2} = E K . E G\).

b) Từ \(\frac{1}{A E} = \frac{1}{A K} + \frac{1}{A G}\) suy ra \(\frac{A E}{A K} + \frac{A E}{A G} = 1\)

\(\Delta A D E\) có \(A D\) // \(B C\) suy ra \(\frac{A E}{E K} = \frac{E D}{E B}\)

     \(\frac{A E}{A E + E K} = \frac{E D}{E D + E B}\)

     \(\frac{A E}{A K} = \frac{E D}{D B}\) (3)

Tương tự \(\Delta A E B\) có \(A B\) // \(D G\) suy ra \(\frac{A E}{E G} = \frac{B E}{E D}\)

     \(\frac{A E}{A E + E G} = \frac{B E}{B E + E D}\)

     \(\frac{A E}{A G} = \frac{B E}{B D}\) (4)

Khi đó \(\frac{A E}{A K} + \frac{A E}{A G} = \frac{E D}{B D} + \frac{B E}{B D} = 1\).

c) Ta có \(\frac{B K}{K C} = \frac{A B}{C G}\) suy ra \(B K = \frac{K C . A B}{C G}\) và \(\frac{K C}{A D} = \frac{C G}{D G}\).

Suy ra \(D G = \frac{A D . C G}{K C}\)

Nhân theo vế ta được \(B K . D G = A B . A D\) không đổi.

a) \(\Delta A B E\) có \(A M\) // \(D G\) suy ra \(\frac{A E}{E G} = \frac{E B}{E D}\) (1)

\(\Delta A D E\) có \(A D\) // \(B K\) suy ra \(\frac{E B}{E D} = \frac{E K}{E A}\) (2)

Từ (1) và (2) ta có \(\frac{A E}{E G} = \frac{E K}{E A}\) nên \(A E^{2} = E K . E G\).

b) Từ \(\frac{1}{A E} = \frac{1}{A K} + \frac{1}{A G}\) suy ra \(\frac{A E}{A K} + \frac{A E}{A G} = 1\)

\(\Delta A D E\) có \(A D\) // \(B C\) suy ra \(\frac{A E}{E K} = \frac{E D}{E B}\)

     \(\frac{A E}{A E + E K} = \frac{E D}{E D + E B}\)

     \(\frac{A E}{A K} = \frac{E D}{D B}\) (3)

Tương tự \(\Delta A E B\) có \(A B\) // \(D G\) suy ra \(\frac{A E}{E G} = \frac{B E}{E D}\)

     \(\frac{A E}{A E + E G} = \frac{B E}{B E + E D}\)

     \(\frac{A E}{A G} = \frac{B E}{B D}\) (4)

Khi đó \(\frac{A E}{A K} + \frac{A E}{A G} = \frac{E D}{B D} + \frac{B E}{B D} = 1\).

c) Ta có \(\frac{B K}{K C} = \frac{A B}{C G}\) suy ra \(B K = \frac{K C . A B}{C G}\) và \(\frac{K C}{A D} = \frac{C G}{D G}\).

Suy ra \(D G = \frac{A D . C G}{K C}\)

Nhân theo vế ta được \(B K . D G = A B . A D\) không đổi.

Bài 1

Cho \(A^{'}\), \(B^{'}\), \(C^{'}\) nằm trên các cạnh \(B C\), \(A C\), \(A B\) của \(\Delta\)ABC, biết \(A A^{'}\), \(B B^{'}\), \(C C^{'}\) đồng quy tại \(M\). Chứng minh rằng \(\frac{A M}{A^{'} M} = \frac{A B^{'}}{C B^{'}} + \frac{A C^{'}}{B C^{'}}\).

Hướng dẫn giải:

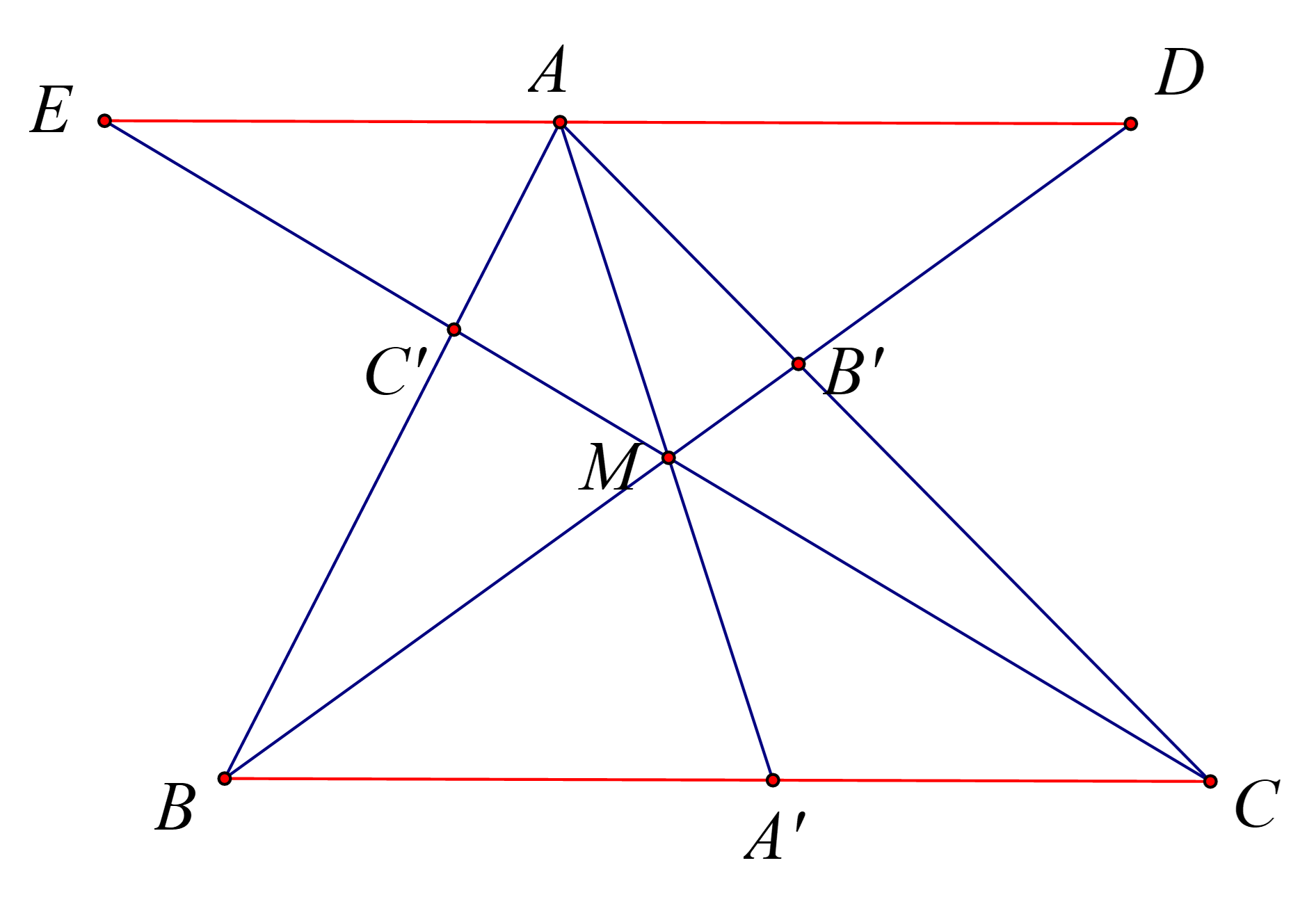
Qua \(A\) vẽ đường thẳng song song với \(B C\) cắt \(B B^{'}\) tại \(D\) và cắt \(C C^{'}\) tại \(E\).

Khi đó 

\(\Delta A M E\) có \(A E\) // \(A^{'} C\) suy ra \(\frac{A M}{A^{'} M} = \frac{A E}{A^{'} C}\) (1)

\(\Delta A M D\) có \(A D\) // \(A^{'} B\) suy ra \(\frac{A M}{A^{'} M} = \frac{A D}{A^{'} B}\) (2)

Từ (1) và (2) ta có \(\frac{A M}{A^{'} M} = \frac{A E}{A^{'} C} = \frac{A D}{A^{'} B} = \frac{A D + A E}{A^{'} C + A^{'} B} = \frac{D E}{B C}\) (*)

Chứng minh tương tự ta cũng có:

\(\Delta A B^{'} D\) có \(A D\) // \(B C\) suy ra \(\frac{A B^{'}}{B^{'} C} = \frac{A D}{B C}\) (3)

\(\Delta A C^{'} E\) có \(A E\) // \(B C\) suy ra \(\frac{A C^{'}}{C^{'} B} = \frac{A E}{B C}\) (4)

Từ (3) và (4) ta có \(\frac{A B^{'}}{B^{'} C} + \frac{A C^{'}}{B C^{'}} = \frac{A D}{B C} + \frac{A E}{B C} = \frac{D E}{B C}\) (**)

Từ (*) và (**) ta có \(\frac{A M}{A^{'} M} = \frac{D E}{B C} = \frac{A B^{'}}{B^{'} C} + \frac{A C^{'}}{B C^{'}}\) (đpcm).

 Môi trường trên cạn: nấm linh chi, xương rồng, hươu cao cổ, chim bồ câu.

- Môi trường dưới nước: cá đuối, bạch tuộc.

- Môi trường trong đất: giun đất, dế trũi.

- Môi trường sinh vật: sâu đục thân, vi khuẩn E. coli​

Biện pháp để hệ sinh thái không bị ô nhiễm nặng hơn: đánh bắt bớt tôm và cá nhỏ hoặc thả thêm vào đầm một số cá dữ để ăn tôm và cá nhỏ → tạo điều kiện cho động vật phù du phát triển mạnh hơn để ăn vi khuẩn lam và tảo → ngăn chặn sự phát triển quá mức của tảo, vi khuẩn lam trong đầm.

Ngoài ra có thể hạn chế nguồn thức ăn của vi khuẩn lam và tảo bằng cách tháo nước, nạo vét bùn ở đáy đầm để loại bỏ bớt các chất gây ô nhiễm.

- Quần thể A: số lượng cá thể thuộc nhóm tuổi trước sinh sản nhỏ hơn so với nhóm tuổi sinh sản → tháp suy thoái.

- Quần thể B: số lượng cá thể thuộc nhóm tuổi trước sinh sản tương đương so với nhóm tuổi sinh sản → tháp ổn định.

- Quần thể C: số lượng cá thể thuộc nhóm tuổi trước sinh sản lớn hơn nhiều so với nhóm tuổi sinh sản → tháp phát triển.

* Vẽ cấu trúc thành phần nhóm tuổi của các quần thể A, B, C