Trong mặt phẳng với hệ trục tọa độ Oth, quỹ đạo của quả bóng là một cung Parabol được xác định bởi hàm số bậc hai:  h=at2+bt+c;(a≠0)h=at2+bt+c;(a=0)  

Từ giả thiết ta có:

{ h(0)=1 h(1)=8,5 h(2)=6⎩⎨⎧​   ​h(0)=1h(1)=8,5h(2)=6​

⇔{ c=1 a+b+c=8,5 4a+2b+c=6⇔⎩⎨⎧​   ​c=1a+b+c=8,54a+2b+c=6​

⇔{ a=−5 b=12,5 c=1⇔⎩⎨⎧​   ​a=−5b=12,5c=1​

Từ đó suy ra h=−5t2+12,5t+1h=−5t2+12,5t+1

Parabol có tọa độ đỉnh là  $I\left(1,25;8,8125\right)$

Độ cao cao nhất của quả bóng đạt được tại đỉnh của cung Parabol.

Vậy $Maxh=8,8125$

Xét f(x)=x2−2x−1f(x)=x2−2x−1

Có a=1>0;Δ′=2>0a=1>0;Δ′=2>0

Suy ra $f\left(x\right)=0$ có hai nghiệm phân biệt x1=1−2;x1​=1−2​; x2=1+2x2​=1+2​.

$f\left(x\right)<0$

⇔x∈(1−2;1+2)⇔x∈(1−2​;1+2​) 

Vậy tập nghiệm là : S=(1−2;1+2)S=(1−2​;1+2​). 

R=d(I,△)=4

vậy pt  đg tròn là (x-7)²+(y-2)²=16

a) −2x2+18x+20≥0−2x2+18x+20≥0

Phương trình: −2x2+18x+20=0−2x2+18x+20=0 có $2$ nghiệm  x1=−1,x2=10x1​=−1,x2​=10

Lập bảng xét dấu f(x)=−2x2+18x+20f(x)=−2x2+18x+20

Vậy $S=[-1,10]$.

b) 2x2−8x+4=x−22x2−8x+4​=x−2

Bình phương hai vế được phương trình: 2x2–8x+4=(x–2)22x2–8x+4=(x–2)2

Rút gọn được phương trình: x2–4x=0x2–4x=0 có hai nghiệm x1=0,x2=4x1​=0,x2​=4.

Thử lại nghiệm được $x=4$ thỏa mãn phương trình. Vậy $S=4$.

Gọi chiều dài đoạn dây điện kéo từ $A$ đến $B$ là $AB=x$ (km).

Khi đó chiều dài dây điện kéo từ $B$ đến $C$ là BC=1+(5−x)2=x2−10x+26BC=1+(5−x)2​=x2−10x+26​ (km)

Tổng tiền công là 3x2−10x+26+2x=133x2−10x+26​+2x=13
⇔3x2−10x+26=13−2x⇔3x2−10x+26​=13−2x

⇔{ 13−2x≥0  9(x2−10x+26)=169−52x+4x2⇔{   ​13−2x≥09(x2−10x+26)=169−52x+4x2​

⇔{ x≤132  5x2−38x+65=0⇔⎩⎨⎧​   ​x≤213​5x2−38x+65=0​

⇔{ x≤132  [ x=5  x=135⇔⎩⎨⎧​   ​x≤213​​   ​x=5x=513​​​

⇔x=135⇔x=513​.

Khi đó AB=x=135⇒BC=135AB=x=513​⇒BC=513​(km).

Khi đó tổng chiều dài dây điện đã kéo từ $A$ đến $C$ là:AB+BC=265AB+BC=526​ (km).

a)

VTPT △=(3;4)

VTPT △1=(5,-12) 

cosa=33/65

b) 

(C) có tâm I(3,-2),R=6 

đg thẳng d có dạng 4x−3y+m=0(m≠7)

d tiếp xúc (C) khi và chỉ khi d(I,d)=R⇔12+6+m/5=6

                                                          ⇒$m=-48$(TM), $m=12$ (TM)

Vậy có hai đường thẳng $d$ thỏa mãn là $4x-3y-48=0$ và $4x-3y+12=0$

2 bên viền là: 2x

chiều dài cả khung ảnh là 17+2x

chiều rộng cả khung ảnh là 25+2x

S cả khung ảnh là:(17+2x).(25+2x)=4x²
+84x+425

Để diện tích của cả khung ảnh lớn nhất là $513$ cm2 thì  S=4x2+84x+425≤513S=4x2+84x+425≤513

                                              ⇒4x
²+84x−88≤0⇔−22≤x≤1. Vì $x>0$ nên $x\in (0;1]$

Ta có f(x)=x2+2(m−1)x+m+5f(x)=x2+2(m−1)x+m+5 có Δ′=(m−1)2−(m+5)=m2−3m−4Δ′=(m−1)2−(m+5)=m2−3m−4

Lại có hệ số $a=1>0$.

Để $f(x)$ luôn dương (cùng dấu hệ số $a$) với mọi $x\in \mathbb{R}$ thì Δ′<0Δ′<0 ⇔m2−3m−4<0⇔m2−3m−4<0.

Xét tam thức h(m)=m2−3m−4h(m)=m2−3m−4 có Δm=9−4.(−4)=25>0Δm​=9−4.(−4)=25>0 nên $h(m)$ có hai nghiệm là m1=−1m1​=−1 và m2=4m2​=4.

Ta có bảng xét dấu của $h(m)$:

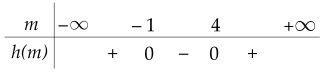
Do đó $h(m)<0$ với mọi $x\in (-1;4)$

Hay Δ′<0Δ′<0 với mọi $x\in (-1;4)$

Vậy $x\in (-1;4)$ thì tam thức bậc hai f(x)=x2+(m−1)x+m+5f(x)=x2+(m−1)x+m+5 dương với mọi $x\in \mathbb{R}$.

b) Bình phương hai vế ta được: 2x2−8x+4=x2−4x+42x2−8x+4=x2−4x+4

⇔x2−4x=0⇔x2−4x=0

Suy ra $x=0$ hoặc $x=4$

Thử lại nghiệm được $x=4$ thỏa mãn phương trình.

Vậy tập nghiệm $S=4$.