a) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 4 chấm" là \(\frac{22}{40}=\frac{11}{20}\)
b) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 6 chấm" là \(\frac{18}{40}=\frac{9}{20}\).

c) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 1 chấm" là \(\frac{14}{40}=\frac{7}{20}\).

d) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 3 chấm" là \(\frac{14}{20}=\frac{7}{10}\).

D(x)=2(x2−x)+(3y2−2y)+(4z2−2z)+2

\(= 2 \left(\right. x^{2} - x + \frac{1}{4} \left.\right) + 3 \left(\right. y^{2} - \frac{2}{3} y + \frac{1}{9} \left.\right) + \left[\right. \left(\right. 2 z \left.\right)^{2} - 2 z + \frac{1}{4} \left]\right. + 2 - \frac{1}{2} - \frac{1}{3} - \frac{1}{4}\)

\(= 2 \left(\left(\right. x - \frac{1}{2} \left.\right)\right)^{2} + 3 \left(\left(\right. y - \frac{1}{3} \left.\right)\right)^{2} + \left(\left(\right. 2 z - \frac{1}{2} \left.\right)\right)^{2} + \frac{11}{2} \geq \frac{11}{2}\)

Vậy giá trị nhỏ nhất của \(D\) là: \(\frac{11}{2}\) tại \(\left(\right. x , y , z \left.\right) = \left(\right. \frac{1}{2} ; \frac{1}{3} ; \frac{1}{4} \left.\right)\).

a) Qua \(D\) vẽ một đường thẳng song song với \(B M\) cắt \(A C\) tại \(N\).

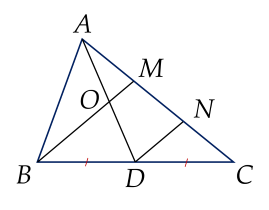
Xét \(\Delta M B C\) có \(D B = D C\) và \(D N\) // \(B M\) nên \(M N = N C = \frac{1}{2} M C\) (định lí đường trung bình của tam giác).

Mặt khác \(A M = \frac{1}{2} M C\), do đó \(A M = M N = \frac{1}{2} M C\).

Xét \(\Delta A N D\) có \(A M = M N\) và \(B M\) // \(D N\) nên \(O A = O D\) hay \(O\) là trung điểm của \(A D\).

b) Xét \(\Delta A N D\) có \(O M\) là đường trung bình nên \(O M = \frac{1}{2} D N\) (1) 

Xét \(\Delta M B C\) có \(D N\) là đường trung bình nên \(D N = \frac{1}{2} B M\). (2)

Từ (1) và (2) ta có \(O M = \frac{1}{4} B M\).

a) Tổng số học sinh của lớp là: 40.

Số học sinh Tốt chiếm số phần trăm là:

     16 : 40 . 100% = 40%

Số học sinh Khá chiếm số phần trăm là:

     11 : 40 . 100% = 27,5%

b) Số học sinh xếp loại Chưa đạt chiếm số phần trăm là:

     3 : 40 . 100% = 7,5%

Cô giáo thông báo tỉ lệ học sinh xếp loại Chưa đạt của lớp chiếm trên 7% là đúng.

Ta có: \(\frac{x - a}{b c} + \frac{x - b}{c a} + \frac{x - c}{a b} = \frac{2}{a} + \frac{2}{b} + \frac{2}{c}\)

\(\left(\right. \frac{x - a}{b c} - \frac{2}{a} \left.\right) + \left(\right. \frac{x - b}{c a} - \frac{2}{b} \left.\right) + \left(\right. \frac{x - c}{a b} - \frac{2}{c} \left.\right) = 0\)

\(\frac{a \left(\right. x - a \left.\right) - 2 b c + b \left(\right. x - b \left.\right) - 2 c a + c \left(\right. x - c \left.\right) - 2 a b}{a b c} = 0\)

Điều kiện xác định: \(a , b , c \neq 0\)

Khi đó: \(\frac{\left(\right. a + b + c \left.\right) x - a^{2} - 2 b c - b^{2} - 2 c a - c^{2} - 2 a b}{a b c} = 0\)

\(\left(\right. a + b + c \left.\right) x = \left(\left(\right. a + b + c \left.\right)\right)^{2}\) 

+ Nếu \(a + b + c = 0\) thì phương trình có vô số nghiệm.

+ Nếu \(a + b + c \neq 0\) thì phương trình có nghiệm duy nhất \(x = a + b + c\).

a) Xét \(\Delta A B E\) và \(\Delta A C F\) có:

\(\hat{B A C}\) chung;

\(\hat{A E B} = \hat{A F C} = 90^{\circ}\);

Do đó \(\Delta A B E \sim \Delta A C F\) (g.g).

Suy ra \(\frac{A B}{A C} = \frac{A E}{A F}\) nên \(A B . A F = A C . A E\).

b) Từ \(A B . A F = A C . A E\) suy ra \(\frac{A E}{A F} = \frac{A B}{A C}\).

Xét \(\Delta A E F\) và \(\Delta A B C\) có:

\(\frac{A E}{A F} = \frac{A B}{A C}\) (cmt);

\(\hat{B A C}\) chung;

Do đó \(\Delta A E F \sim \Delta A B C\) (c.g.c)

Suy ra \(\hat{A F E} = \hat{A C B}\) (cặp góc tương ứng).

c) Xét \(\Delta C E B\) và \(\Delta C D A\) có:

\(\hat{A C B}\) chung;

\(\hat{C E B} = \hat{C D A} = 90^{\circ}\)

Do đó \(\Delta C E B \sim \Delta C D A\) (g.g)

Suy ra \(\frac{C B}{C E} = \frac{C A}{C D}\) (cặp cạnh tương ứng).

Xét \(\Delta C B A\) và \(\Delta C E D\) có:

\(\frac{C B}{C E} = \frac{C A}{C D}\) (cmt);

\(\hat{A C B}\) chung;

Do đó \(\Delta C B A \sim \Delta C E D\) (c.g.c)

Suy ra \(\hat{C D E} = \hat{C A B}\) (cặp góc tương ứng) (1)

Tương tự: \(\hat{B D F} = \hat{C A B}\) (2).

Từ (1) và (2) suy ra \(\hat{C D E} = \hat{B D F}\).

Mà \(\hat{C D E} + \hat{E D A} = \hat{B D F} + \hat{F D A}\) suy ra \(\hat{E D A} = \hat{F D A}\).

Suy ra \(D A\) là phân giác của góc \(E D F\).

Mặt khác \(A D \bot K D\) nên \(D K\) là phân giác ngoài của \(\Delta D E F\).

Ta có \(D I\) là phân giác trong của \(\Delta \&\text{nbsp}; D E F\) suy ra \(\frac{I F}{I E} = \frac{D F}{D E}\) (3)

Ta có \(D K\) là phân giác ngoài của \(\Delta D E F\) suy ra \(\frac{K F}{K E} = \frac{D F}{D E}\) (4)

Từ (3) và (4) suy ra \(\frac{I F}{I E} = \frac{K F}{K E}\).

a) Xét \(\Delta A B E\) và \(\Delta A C F\) có:

\(\hat{B A C}\) chung;

\(\hat{A E B} = \hat{A F C} = 90^{\circ}\);

Do đó \(\Delta A B E \sim \Delta A C F\) (g.g).

Suy ra \(\frac{A B}{A C} = \frac{A E}{A F}\) nên \(A B . A F = A C . A E\).

b) Từ \(A B . A F = A C . A E\) suy ra \(\frac{A E}{A F} = \frac{A B}{A C}\).

Xét \(\Delta A E F\) và \(\Delta A B C\) có:

\(\frac{A E}{A F} = \frac{A B}{A C}\) (cmt);

\(\hat{B A C}\) chung;

Do đó \(\Delta A E F \sim \Delta A B C\) (c.g.c)

Suy ra \(\hat{A F E} = \hat{A C B}\) (cặp góc tương ứng).

c) Xét \(\Delta C E B\) và \(\Delta C D A\) có:

\(\hat{A C B}\) chung;

\(\hat{C E B} = \hat{C D A} = 90^{\circ}\)

Do đó \(\Delta C E B \sim \Delta C D A\) (g.g)

Suy ra \(\frac{C B}{C E} = \frac{C A}{C D}\) (cặp cạnh tương ứng).

Xét \(\Delta C B A\) và \(\Delta C E D\) có:

\(\frac{C B}{C E} = \frac{C A}{C D}\) (cmt);

\(\hat{A C B}\) chung;

Do đó \(\Delta C B A \sim \Delta C E D\) (c.g.c)

Suy ra \(\hat{C D E} = \hat{C A B}\) (cặp góc tương ứng) (1)

Tương tự: \(\hat{B D F} = \hat{C A B}\) (2).

Từ (1) và (2) suy ra \(\hat{C D E} = \hat{B D F}\).

Mà \(\hat{C D E} + \hat{E D A} = \hat{B D F} + \hat{F D A}\) suy ra \(\hat{E D A} = \hat{F D A}\).

Suy ra \(D A\) là phân giác của góc \(E D F\).

Mặt khác \(A D \bot K D\) nên \(D K\) là phân giác ngoài của \(\Delta D E F\).

Ta có \(D I\) là phân giác trong của \(\Delta \&\text{nbsp}; D E F\) suy ra \(\frac{I F}{I E} = \frac{D F}{D E}\) (3)

Ta có \(D K\) là phân giác ngoài của \(\Delta D E F\) suy ra \(\frac{K F}{K E} = \frac{D F}{D E}\) (4)

Từ (3) và (4) suy ra \(\frac{I F}{I E} = \frac{K F}{K E}\).

a) Với �=−1m=−1, hàm số trở thành �=−2�+1y=−2x+1.

Xét hàm số �=−2�+1y=−2x+1 :

Thay �=0x=0 thì �=1y=1.

Suy ra đồ thị hàm số �=−2�+1y=−2x+1 đi qua điểm có tọa độ (0;1)(0;1).

Thay �=1x=1 thì �=−1y=−1.

 Vì đường thẳng (�):�=��+�(d):y=ax+b song song với đường thẳng (�′ ):�=−3�+9(d′ ):y=−3x+9 nên: �≠−3;�≠9a=−3;b=9.

Khi đó ta có: (�):�=−3�+�(d):y=−3x+b và �≠9b
 khác 9.

Vì đường thẳng (�):�=��+�(d):y=ax+b đi qua �(1;−8)A(1;−8) nên: −8=−3.1+�−8=−3.1+b

Suy ra �=−5b=−5 (thoả mãn)

Vậy đường thẳng cần tìm là (�):�=−3�−5(d):y=−3x−5.

Suy ra đồ thị hàm số �=−2�+1y=−2x+1 đi qua điểm có tọa độ (1;−1)(1;−1).

Vẽ đồ thị:

 Vì đường thẳng (�):�=��+�(d):y=ax+b song song với đường thẳng (�′ ):�=−3�+9(d′ ):y=−3x+9 nên: �≠−3;�≠9a
 khác−3;b
 khác 9.

Khi đó ta có: (�):�=−3�+�(d):y=−3x+b và �≠9b
 khác 9.

Vì đường thẳng (�):�=��+�(d):y=ax+b đi qua �(1;−8)A(1;−8) nên: −8=−3.1+�−8=−3.1+b

Suy ra �=−5b=−5 (thoả mãn)

Vậy đường thẳng cần tìm là (�):�=−3�−5(d):y=−3x−5.

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)

20 phút = 1/3 h

Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)

Quãng đường đi từ thành phố về quê: 30x (km)

Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)

Theo đề bài, ta có phương trình:

30x = 25(x + 1/3)

30x = 25x + 25/3

30x - 25x = 25/3

5x = 25/3

x = 25/3 : 5

x = 5/3 (nhận)

Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a)3x=9

x=3

vậy pt có nghiệm x=3

b)\(\frac{\left(2x\right)*2}{6}\) +\(\frac{3X-1}{6}\) =\(\frac{3x}{6}\)

=)4X+3x-1=3x

=)4x+3x-3x=1

=)4x=1

=)x=\(\frac14\)

Vậy pt có nghiệm x=\(\frac14\)