Xét \(\Delta A B C\) vuông tại \(B\), ta có:

\(tan ⁡ \hat{B A C} = \frac{B C}{A B} = \frac{2}{2 , 5} = 0 , 8\) (tỉ số lượng giác của góc nhọn)

Suy ra \(\hat{B A C} \approx 38 , 7^{\circ}\)

Ta có: \(\hat{B A D} = \hat{B A C} + \hat{C A D} = 38 , 7^{\circ} + 2 0^{\circ} = 58 , 7^{\circ}\)

Xét \(\Delta A B D\) vuông tại \(B\), ta có:

\(tan ⁡ \hat{B A D} = \frac{B D}{A B}\) (tỉ số lượng giác của góc nhọn)

Suy ra \(B D = A B . tan ⁡ \hat{B A D} = 2 , 5. tan ⁡ 58 , 7^{\circ} \approx 4 , 1\) m.

\(C D = B D - B C = 4 , 1 - 2 = 2 , 1\) m.

Vậy độ dài vùng được chiếu sáng trên mặt đất là \(2 , 1\) m.

1)  \(sin ⁡ 3 5^{\circ} = cos ⁡ \left(\right. 9 0^{\circ} - 3 5^{\circ} \left.\right) = cos ⁡ \&\text{nbsp}; 5 5^{\circ}\);

\(tan ⁡ 2 8^{\circ} = cot ⁡ \left(\right. 9 0^{\circ} - 2 8^{\circ} \left.\right) = cot ⁡ 6 2^{\circ}\).

2) Xét \(\Delta A B C\) vuông tại \(A\), ta có:

\(B C = 20\)

\(cos ⁡ \hat{B} = \frac{A B}{B C} = \frac{A B}{20} = cos ⁡ 3 6^{\circ}\)

Suy ra \(A B = B C . cos ⁡ 3 6^{\circ} \approx 16 , 18\) cm.

1)  \(sin ⁡ 3 5^{\circ} = cos ⁡ \left(\right. 9 0^{\circ} - 3 5^{\circ} \left.\right) = cos ⁡ \&\text{nbsp}; 5 5^{\circ}\);

\(tan ⁡ 2 8^{\circ} = cot ⁡ \left(\right. 9 0^{\circ} - 2 8^{\circ} \left.\right) = cot ⁡ 6 2^{\circ}\).

2) Xét \(\Delta A B C\) vuông tại \(A\), ta có:

\(B C = 20\)

\(cos ⁡ \hat{B} = \frac{A B}{B C} = \frac{A B}{20} = cos ⁡ 3 6^{\circ}\)

Suy ra \(A B = B C . cos ⁡ 3 6^{\circ} \approx 16 , 18\) cm.

1)  \(sin ⁡ 3 5^{\circ} = cos ⁡ \left(\right. 9 0^{\circ} - 3 5^{\circ} \left.\right) = cos ⁡ \&\text{nbsp}; 5 5^{\circ}\);

\(tan ⁡ 2 8^{\circ} = cot ⁡ \left(\right. 9 0^{\circ} - 2 8^{\circ} \left.\right) = cot ⁡ 6 2^{\circ}\).

2) Xét \(\Delta A B C\) vuông tại \(A\), ta có:

\(B C = 20\)

\(cos ⁡ \hat{B} = \frac{A B}{B C} = \frac{A B}{20} = cos ⁡ 3 6^{\circ}\)

Suy ra \(A B = B C . cos ⁡ 3 6^{\circ} \approx 16 , 18\) cm.

1)  \(sin ⁡ 3 5^{\circ} = cos ⁡ \left(\right. 9 0^{\circ} - 3 5^{\circ} \left.\right) = cos ⁡ \&\text{nbsp}; 5 5^{\circ}\);

\(tan ⁡ 2 8^{\circ} = cot ⁡ \left(\right. 9 0^{\circ} - 2 8^{\circ} \left.\right) = cot ⁡ 6 2^{\circ}\).

2) Xét \(\Delta A B C\) vuông tại \(A\), ta có:

\(B C = 20\)

\(cos ⁡ \hat{B} = \frac{A B}{B C} = \frac{A B}{20} = cos ⁡ 3 6^{\circ}\)

Suy ra \(A B = B C . cos ⁡ 3 6^{\circ} \approx 16 , 18\) cm.

a) Tính giá trị của biểu thức $A$ khi $x=4.$

Thay $x=4$ (thỏa mãn điều kiện) vào biểu thức $A$ ta được:

A=24−1=2.A=4​−12​=2.

b) Với $x\ge 0,x\ne 1$ ta có P=B−A=xx+1+4x−1−2x−1P=B−A=x​+1x​​+x−14​−x​−12​

=x(x−1)+4−2(x+1)(x−1)(x+1)=(x​−1)(x​+1)x​(x​−1)+4−2(x​+1)​

=x−3x+2(x−1)(x+1)=(x​−1)(x​+1)x−3x​+2​

=(x−1)(x−2)(x−1)(x+1)=(x​−1)(x​+1)(x​−1)(x​−2)​

=x−2x+1.=x​+1x​−2​.

c) Với $x\ge 0,x\ne 1$ ta có P=x−2x+1=1−3x+1.P=x​+1x​−2​=1−x​+13​.

x+1≥1x​+1≥1 với mọi $x$ thỏa mãn điều kiện nên 3x+1≤3x​+13​≤3 suy ra $P\ge -2.$

Dấu bằng xảy ra khi và chỉ khi $x=0$ (thỏa mãn điều kiện).

Vậy giá trị nhỏ nhất của biểu thức $P=-2$ khi $x=0.$

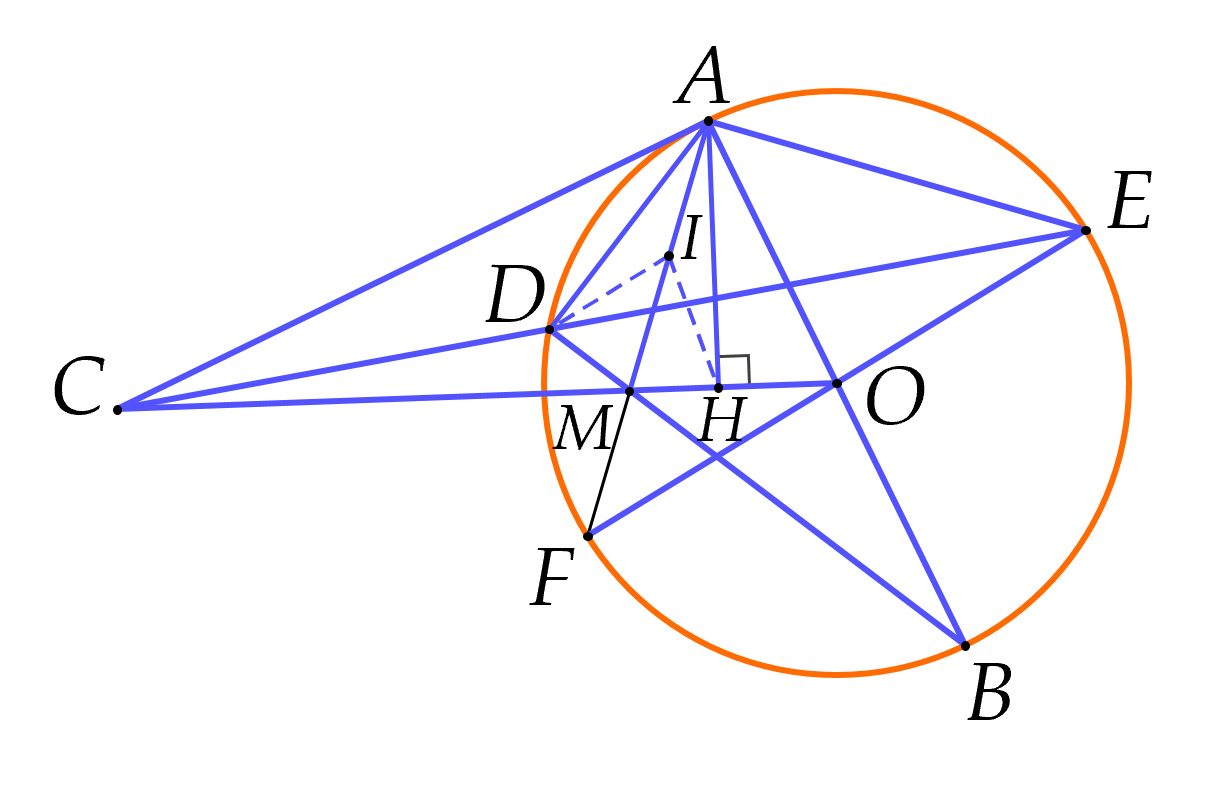
a) Gọi $I$ là trung điểm của $AM$.

Ta có ADB^=90∘ADB=90∘ (góc nội tiếp chắn nửa đường tròn) hay ADM^=90∘ADM=90∘

Suy ra $\Delta ADM$ là tam giác vuông tại $D$ có $DI$ là đường trung tuyến nên AI=DI=MI=AM2AI=DI=MI=2AM​ (1)

Do $H$ là hình chiếu vuông góc của điểm $A$ trên $CO$ nên $AH\perp CO$

Suy ra $\Delta AHM$ là tam giác vuông tại $H$ có $HI$ là đường trung tuyến nên: AI=HI=MI=AM2AI=HI=MI=2AM​ (2)

Từ (1) và (2) suy ra $AI=DI=MI=HI$,

Do đó bốn điểm $A;D;M;H$ cùng thuộc một đường tròn.

Vậy $ADMH$ là tứ giác nội tiếp.

b) Ta có CAD^+DAO^=90∘CAD+DAO=90∘

CEA^+CEB^=AEB^=90∘CEA+CEB=AEB=90∘ (góc nội tiếp chắn nửa đường tròn).

Mà DAO^=CEB^DAO=CEB (cùng chắn DB⌢DB⌢)

Do đó CAD^=CEA^CAD=CEA

Do đó $\Delta CAD\backsim \Delta CEA$ (g.g)

Suy ra CACE=CDCACECA​=CACD​ hay CA2=CD.CECA2=CD.CE (1)

 Mặt khác $\Delta ACO\backsim \Delta HCA$ (g.g)

Suy ra CA2=CH.COCA2=CH.CO (2)

Từ (1) và (2) suy ra: $CD.CE=CH.CO$.

Gọi giao điểm hai đường chéo của hình chữ nhật là $O$.

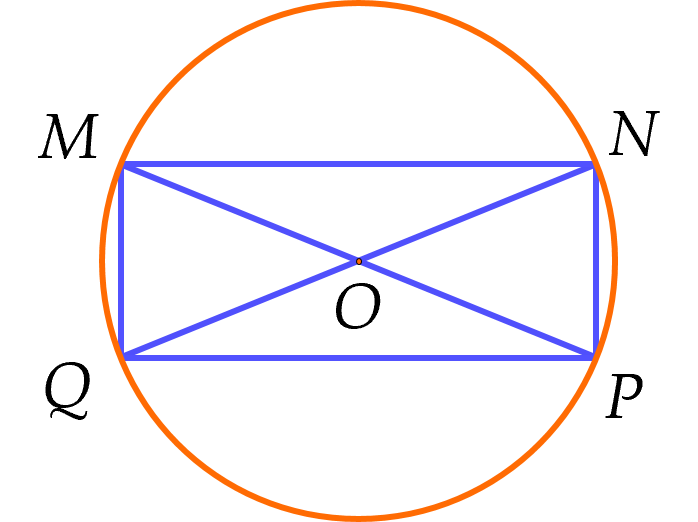
Gọi $x,y$ (m) lần lượt là hai kích thước của mảnh vườn $(x>0,y>0)$ và $R$ (m) là bán kính đường tròn ngoại tiếp mảnh vườn.

Áp dụng định lí Pythagore trong tam giác vuông $MNP$, ta có:

x2+y2=MP2x2+y2=MP2

Suy ra R2=OM2=x2+y24R2=OM2=4x2+y2​

Theo đề bài $xy=640$ m2

Diện tích $4$ phần đất mở rộng là: S=St−SMNPQ=πR2−xy=π.(x2+y24)−xy≥π.2xy4−xyS=St​−SMNPQ​=πR2−xy=π.(4x2+y2​)−xy≥π.42xy​−xy (theo bất đẳng thức Cauchy)

Do đó $S\ge 320\pi -640\approx 365,31$ m2.

Dấu "=" xảy ra khi x=y=810x=y=810​ (thoả mãn).

Vậy diện tích nhỏ nhất của $4$ phần đất được trồng thêm hoa khoảng $365,31$ m2.

Vì các điểm phân biệt nằm trên một đường tròn nên ba điểm bất kì luôn tạo thành một tam giác.

Có 21 điểm được tô bằng 4 màu, do đó có ít nhất 6 điểm có cùng màu.

Giả sử có 6 điểm cùng màu đỏ là $A,B,C,D,E,F$

Nối 5 đoạn $AB,AC,AD,AE,AF$ và tô bằng hai màu nâu, đen khi đó có ít nhất 3 đoạn cùng màu, giả sử $AB,AC,AD$ được tô cùng màu đen

Xét $\Delta BCD$, xảy ra hai khả năng:

TH1: Nếu 3 cạnh $BC,BD,DC$ được tô cùng màu nâu thì tam giác $BCD$ có ba đỉnh cùng màu đỏ, ba cạnh cùng màu nâu (thỏa mãn)

TH2: Nếu ba cạnh $BC,BD,DC$ có ít nhất một cạnh màu đen, giả sử $BC$ đen, khi đó tam giác $ABC$ có ba đỉnh cùng màu đỏ, ba cạnh cùng màu đen (thỏa mãn)

Vậy luôn có một tam giác có ba đỉnh cùng màu và ba cạnh cùng màu.

4536