

ĐẶNG XUÂN MINH
Giới thiệu về bản thân




































Lấy D là trung điểm của cạnh BC.
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có AGAD=23ADAG=32 hay AG=23ADAG=32AD
Vì MG // AB, theo định lí Thalès, ta suy ra: AGAD=BMBD=23ADAG=BDBM=32
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên BMBC=BM2BD=22.3=13BCBM=2BDBM=2.32=31
Do đó BM=13BCBM=31BC (đpcm).
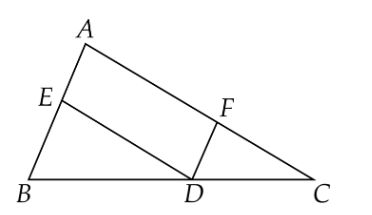
xét △ABC△ABC có:
@ED////AC=>[AE]/[AB]=[DC]/[BC]ED////AC=>AE/AB=DC/BC
@DF////AB=>[AF]/[AC]=[BD]/[BC]DF////AB=>AF/AC]=BD/BC
=>[AE]/[AB]+[AF]/[AC]=[DC+BD]/[BC]=[BC]/[BC]=1=>AE/AB+AF/AC=DC+BD/BC=BC/BC=1 (đpcm)(đpcm).
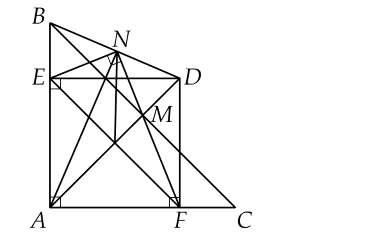
a) Chứng minh AEDF là hình vuông:
- Ta có: ΔABC vuông cân tại A (gt) => ∠BAC = 90 độ, AB = AC
- AE ⊥ AB, AF ⊥ AC (gt) => ∠AED = ∠AFD = 90 độ
- Tứ giác AEDF có 3 góc vuông nên AEDF là hình chữ nhật.
- Mà AD là đường chéo của hình chữ nhật AEDF (vì AD là đường trung trực của BC) => AEDF là hình vuông (hình chữ nhật có hai đường chéo bằng nhau).
b) Chứng minh EF // BC:
- Ta có: AEDF là hình vuông (cmt) => EF // AD (tính chất hình vuông)
- Mà AD // BC (do AM là đường trung bình của ΔABC) => EF // BC.
c) Chứng minh góc AND = 90 độ:
- Kẻ đường thẳng qua M vuông góc với EF cắt EF tại H.
- Ta có: MH ⊥ EF, AD ⊥ EF (vì AEDF là hình vuông) => MH // AD
- Mà M là trung điểm của BC => H là trung điểm của EF (đường trung bình của tam giác)
- Xét ΔMEF có:
- MH là đường trung trực của EF (vì MH ⊥ EF tại trung điểm H)
- EN ⊥ MF (gt) => AN là đường trung trực của MF (tính chất ba đường vuông góc) => AN ⊥ MF
- Mà MH // AD => AN ⊥ AD => Góc AND = 90 độ.
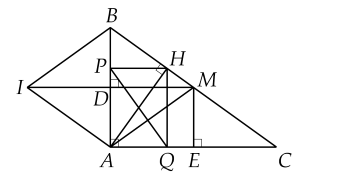 a) Chứng minh ADME là hình chữ nhật:
a) Chứng minh ADME là hình chữ nhật:
- Ta có: MD vuông góc AB, ME vuông góc AC (gt)
- Suy ra: Góc ADM = góc AEM = 90 độ
- Tứ giác ADME có ba góc vuông nên ADME là hình chữ nhật.
- Vì D là trung điểm của IM nên AD = DM.
- Mà AD = ME (ADME là hình chữ nhật)
- Suy ra: DM = ME
- Tứ giác AMBE có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường nên AMBE là hình thoi.
- Để hình thoi AMBE là hình vuông thì AM phải vuông góc với BE.
- Mà AM là đường trung tuyến của tam giác vuông ABC nên AM cũng là đường cao.
- Vậy để AMBI là hình vuông thì tam giác ABC phải là tam giác vuông cân tại A.
- Ta có: HP vuông góc AB, HQ vuông góc AC (gt)
- Suy ra: HP // ME (cùng vuông góc AB), HQ // MD (cùng vuông góc AC)
- Tứ giác PHEQ là hình bình hành (hai cặp cạnh đối song song)
- Mà ADME là hình chữ nhật nên AE = DM
- Suy ra: PE = QM (do PHEQ là hình bình hành)
- Tứ giác PQME có PE = QM và PQ // ME nên PQME là hình bình hành.
- Mà ADME là hình chữ nhật nên AM vuông góc DE.
- Suy ra: AM vuông góc PQ (do PQME là hình bình hành).
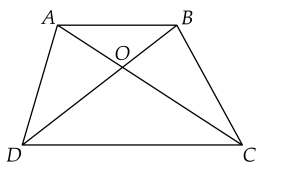
a) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Ta có ; // suy ra .
Tứ giác có ba góc vuông nên là hình chữ nhật.
Khi đó hai đường chéo cắt nhau tại trung điểm của mỗi đường, mà nên là trung điểm của .
Suy ra thẳng hàng.
c) Để tứ giác là hình vuông thì ta cần hay vuông cân tại
a) Chứng minh MCDN là hình thoi: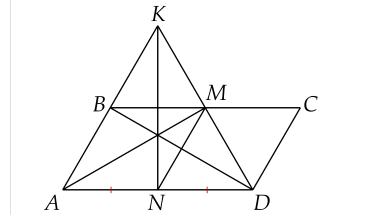
- Xét tứ giác ABCD:
- ABCD là hình bình hành (gt)
- Góc BAD = 60 độ (gt)
- AD = 2AB (gt)
- Suy ra: ABCD là hình thoi (hình bình hành có hai cạnh kề bằng nhau)
- Xét tam giác ABD:
- AB = BD (ABCD là hình thoi)
- AN = ND (N là trung điểm AD)
- Suy ra: BN là đường trung trực của AD
- Tương tự, CM là đường trung trực của BD
- Gọi O là giao điểm của BN và CM:
- O là trung điểm của AD và BD
- Suy ra: O là tâm đối xứng của hình thoi ABCD
- Xét tứ giác MCDN:
- MD // NC (MN là đường trung bình của hình thang ABCD)
- MD = NC (MN là đường trung bình của hình thang ABCD)
- Suy ra: MCDN là hình bình hành (hai cạnh đối song song và bằng nhau)
- Mà O là trung điểm của MN (O là tâm đối xứng của ABCD)
- Suy ra: MCDN là hình thoi (hình bình hành có hai đường chéo vuông góc)
b) Chứng minh ABMD là hình thang cân và AM = BD:
- Xét tam giác ABD:
- AB = BD (ABCD là hình thoi)
- Góc BAD = 60 độ (gt)
- Suy ra: Tam giác ABD đều
- Xét tứ giác ABMD:
- AB // MD (ABCD là hình bình hành)
- AB ≠ MD (AD = 2AB)
- Suy ra: ABMD là hình thang
- Mà góc DAB = 60 độ (gt)
- Suy ra: ABMD là hình thang cân
- Ta có:
- AM là đường trung tuyến của tam giác đều ABD
- Suy ra: AM cũng là đường cao của tam giác ABD
- Suy ra: AM vuông góc với BD
- Mà BD = AB (ABCD là hình thoi)
- Suy ra: AM = BD (đường vuông góc kẻ từ một điểm đến một đường thẳng cho đoạn thẳng ngắn nhất)
c) Chứng minh AM, DB, KN đồng quy:
- Gọi I là giao điểm của AM và BD:
- I là trung điểm của BD (AM là đường trung trực của BD)
- Xét tam giác AKD:
- N là trung điểm của AD
- I là trung điểm của BD
- Suy ra: NI là đường trung bình của tam giác AKD
- Suy ra: NI // AK
- Mà NI cũng đi qua O (O là tâm đối xứng của ABCD)
- Suy ra: K, O, N thẳng hàng
- Vậy AM, DB, KN đồng quy tại O.
a) Chứng minh ΔAOP = ΔBOR:
- Xét ΔAOP và ΔBOR, ta có:
- OA = OB (tính chất hình vuông)
- ∠AOP = ∠BOR (đối đỉnh)
- ∠OAP = ∠OBR = 90° (do m vuông góc với AB và BC)
- Theo trường hợp góc - cạnh - góc, ta có ΔAOP = ΔBOR.
b) Chứng minh OP = OR = OS = OQ:
- Từ ΔAOP = ΔBOR, suy ra OP = OR.
- Tương tự, ta chứng minh được ΔAOS = ΔDOQ (g-c-g), suy ra OS = OQ.
- Mà OP = OR và OS = OQ, nên OP = OR = OS = OQ.
c) Chứng minh PRQS là hình vuông:
- Ta có:
- PQ // SR (cùng vuông góc với m)
- PS // QR (cùng vuông góc với n)
- PQ = SR (do ΔAOP = ΔBOR và ΔAOS = ΔDOQ)
- PS = QR (do ΔAOP = ΔBOR và ΔAOS = ΔDOQ)
- Từ các điều kiện trên, suy ra tứ giác PRQS là hình bình hành.
- Mà OP = OR = OS = OQ (chứng minh ở câu b), nên PRQS là hình thoi.
- Hình thoi có một góc vuông (∠PQR = 90°) nên PRQS là hình vuông.
a) Tứ giác DKMN có 3 góc D=K=N= 90 độ
=> Tg DKMN là hình chữ nhật
Vậy tg DKMN là hình chữ nhật
b) Vì DKMN là hình chữ nhật nên DF//MH
Xét 2 tam giác KFM và NME có:
góc K= góc N = 90 độ
FM=ME(gt)
góc KMF = góc E( đồng vị)
=> Tam giác KFM = tam giác NME (cạnh huyền-góc nhọn)
=>KF=MN( hai cạnh tương ứng) mà MN=DK nên DF=2DK và MH=2MN
Do đó DF=MH
Tứ gáic DFMH có DF//MH, DF=MH nên là hình bình hành
Do đó hai đường chéo DM,FH cắt nhau tại trung điểm O của mỗi đường hay F,O,H thẳng hàng
Vậy 3 điểm F,O,H thẳng hàng
c) Để hình chữ nhật DKMN là hình vuông thì DK=DN(1)
Mà DK=1/2DF và DN=KM=NE nên DN=1/2DE(2)
Từ (1),(2) suy ra DF=DE
Vậy tam giác DFE cần thêm điều kiện cân tại D
a) Vì suy ra BC= AB/2=AD
ABCD là hình chữ nhật nên AB=DC suy ra 1/2AB=1/2DC do đó AI=DK=AD
Tứ giác AIKD có AI//DK, AI=DK nên tứ giác AIKD là hình bình hành
Lại có AD=AI nên AIKD là hình thoi
Mà góc IAD= 90 độ do đó AIKD là hình vuông
Vậy tứ giác AIKD là hình vuông
Chứng minh tương tự cho tứ giác BIKC
Vậy tứ gáic BIKC là hình vuông
b) VÌ AIKD là hình vuông nên DI là tia phân giác góc ADK nên góc IDK = 45 độ
Tương tự góc ICK = 45 độ
Tam giác IDC cân có góc DIC = 90 độ nên là tam gaic vuông cân
Vậy tam giác IDC là tam gáic vuông cân
c) Vì AIKD, BCKI là các hình vuông nên hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên SI=SK=DI/2 và IR=RK=IC/2
=>ISKR là hình thoi
Lại có góc DIC= 90 độ nên ISKR là hình vuông
Vậy ISKR là hình vuông