ĐẶNG XUÂN MINH
Giới thiệu về bản thân



































Trong tình huống bạn H (15 tuổi) bị bố ép làm việc quá 8 tiếng/ngày ở quán ăn để kiếm tiền gửi cho bố, đây là hành vi bóc lột sức lao động trẻ em và bạo lực gia đình. Để ứng phó với tình huống này, bạn H có thể thực hiện các cách sau:
Tìm kiếm sự giúp đỡ từ người thân, bạn bè đáng tin cậy:
Chia sẻ tình trạng với ông bà, cô, chú hoặc những người thân có thể giúp đỡ.
Nhờ bạn bè giúp đỡ thông báo với giáo viên hoặc người lớn.
Báo với thầy cô hoặc ban giám hiệu nhà trường:
Trình bày rõ sự việc để thầy cô có thể can thiệp, bảo vệ quyền lợi.
Nhà trường sẽ có biện pháp hỗ trợ hoặc thông báo với cơ quan chức năng.
Liên hệ với các tổ chức bảo vệ trẻ em:
Gọi đến tổng đài bảo vệ trẻ em 111 (miễn phí 24/7) để được tư vấn và hỗ trợ.
Nhờ sự giúp đỡ từ các trung tâm bảo trợ xã hội hoặc Hội Bảo vệ Quyền Trẻ em Việt Nam.
Mặc dù lương của bạn H tương đối ổn định, nhưng bạn ấy thường xuyên tiêu xài quá tay vào cuối tháng và phải mượn tiền bạn bè để trang trải. Bạn H đã cố gắng tiết kiệm, nhưng dường như không thể duy trì thói quen chi tiêu hợp lý.
ChatGPT đã nói:
Vấn đề của bạn H là thói quen chi tiêu không hợp lý, đặc biệt vào cuối tháng, dẫn đến việc phải mượn tiền bạn bè dù lương ổn định. Để giúp bạn H cải thiện tình trạng này, có thể đưa ra một số giải pháp sau:
Lập kế hoạch chi tiêu chi tiết:
Phân chia thu nhập theo các khoản cố định (tiền nhà, điện nước, ăn uống) và khoản tiết kiệm.
Giới hạn số tiền cho các nhu cầu giải trí, mua sắm.
Theo dõi chi tiêu hàng ngày:
Ghi lại các khoản chi tiêu nhỏ để nhận biết những khoản không cần thiết.
Sử dụng ứng dụng quản lý tài chính như Money Lover hoặc Sổ Thu Chi.
Thiết lập quỹ khẩn cấp:
Tự động trích một phần lương vào tài khoản tiết kiệm ngay khi nhận lương.
Không sử dụng quỹ này trừ trường hợp thực sự cần thiết.
Hạn chế chi tiêu không cần thiết:
Chỉ mua những món đồ thực sự cần, tránh mua sắm theo cảm xúc.
Lên danh sách trước khi đi mua sắm.
Tìm bạn đồng hành:
Chia sẻ kế hoạch tiết kiệm với bạn bè để được động viên và kiểm soát thói quen chi tiêu.
Bằng cách áp dụng các giải pháp này, bạn H có thể dần thay đổi thói quen chi tiêu và duy trì cuộc sống tài chính lành mạnh hơn.
Xét tam giác ABCABC, áo dụng tính chất tia phân giác trong tam giác, ta có:
AMMB=ACCB=ABCB=ANNC(=ba)MBAM=CBAC=CBAB=NCAN(=ab)
Vậy MNMN // BCBC (Định lí đảo của định lí Thalès)
Suy ra MNBC=AMAB=bb+aBCMN=ABAM=b+ab (Định lí Thalès)
Vậy nên MN=aba+b.MN=a+bab.
Tam giác ABCABC cân tại AA nên AB=AC=12AB=AC=12 cm.
a) Xét tam giác ABCABC, áp dụng tính chất tia phân giác ta có:
ADDB=ACCB=126=2DBAD=CBAC=612=2
Suy ra ADAB=23ABAD=32 suy ra AD=23.12=8AD=32.12=8 (cm)
Do đó, DB=12−8=4DB=12−8=4 (cm).
b) Do CECE vuông góc với phân giác CDCD nên CECE là phân giác ngoài tại đỉnh CC của tam giác ABCABC.
Vậy EBEA=BCACEAEB=ACBC hay EBEB+BA=BCACEB+BAEB=ACBC
Gọi độ dài EBEB là xx thì xx+12=612x+12x=126.
Vậy x=12x=12 (cm).
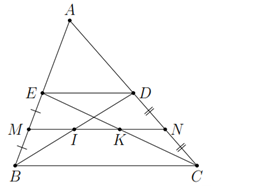
Do BD là đường trung tuyến của ∆ABC (gt)
⇒ D là trung điểm của AC
Do CE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AB
⇒ DE là đường trung bình của ∆ABC
⇒ DE // BC và DE = BC : 2
⇒ BC = 2DE
Do DE // BC (cmt)
⇒ BCDE là hình thang
Do M là trung điểm của BE (gt)
N là trung điểm của CD (gt)
⇒ MN là đường trung bình của hình thang BCDE
⇒ MN // DE // BC và MN = (DE + BC) : 2
Do MN // DE (cmt)
⇒ MI // DE và NK // DE
∆BDE có:
MI // DE (cmt)
M là trung điểm của BE (gt)
⇒ I là trung điểm của BD
⇒ MI là đường trung bình của ∆BDE
⇒ MI = DE : 2 (1)
∆CDE có:
NK // DE (cmt)
N là trung điểm của CD (gt)
⇒ K là trung điểm của CE
⇒ NK là đường trung bình của ∆CDE
⇒ NK = DE : 2 (2)
Mà MI = DE : 2
⇒ MI = NK = DE : 2
⇒ MI + NK = DE
Ta có:
MN = (DE + BC) : 2
Mà BC = 2DE (cmt)
⇒ MN = (DE + 2DE) : 2
= DE + DE : 2
Lại có:
MN = MI + IK + NK
= (MI + NK) + IK
= DE + IK
⇒ DE + IK = DE + DE : 2
⇒ IK = DE : 2 (3)
Từ (1), (2) và (3) ⇒ MI = IK = KN
a/
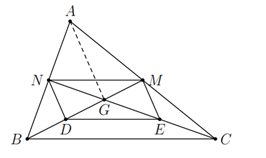
Xét tg ABC có
NA=NB; MA=MC => MN là đường trung bình của tg ABC => MN//BC
Xét tg GBC có
DG=DB; EG=EC => DE là đường trung bình của tg GBC => DE//BC
=> MN//DE (cùng // BC)
b/
Xét tg ABG có
NA=NB; DG=DB => ND là đường trung bình của tg ABG => ND//AG
Xét tg ACG có
MA=MC; EG=EC => ME là đường trung bình của tg ACG => ME//AG
=> ND//ME (cùng // với AG)
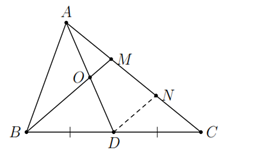
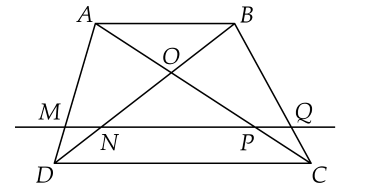
a/ Goi E là trung điểm của MC
Từ gt AM=12MC⇒AM=ME=ECAM=21MC⇒AM=ME=EC
Xét tg BCM có
ME=EC (cmt); DB=DC (gt) => DE là đường trung bình của tg BCM
=> DE//BM
Xét tg ADE có
AM=ME (cmt)
BM//DE (cmt) =>OM//DE
=> OA=OD (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
b/
Ta có DE là đường trung bình của tg BCM ⇒DE=12BM⇒DE=21BM
Xét tg ADE có
OA=OD (cmt); AM=ME (cmt) => OM là đường trung bình của tg ADE
⇒OM=12DE=12.12BM=14BM⇒OM=21DE=21.21BM=41BM
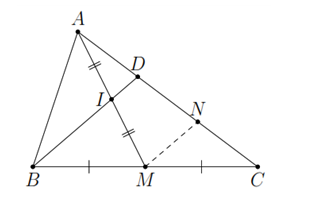
Gọi K là trung điểm của CD
a: Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của CD
Do đó: MK là đường trung bình
=>MK//BD
hay ID//MK
Xét ΔAMK có
I là trung điểm của AM
ID//MK
Do đó: D là trung điểm của AK
=>AD=DK=KC
=>AD=1/2DC
b: Xét ΔAMK có
I là trung điểm của AM
D là trung điểm của AK
Do đó: ID là đường trung bình
=>ID=MK/2
hay MK=2ID
Ta có: MK là đường trung bình của ΔBDC
nên MK=BD/2
=>BD/2=2ID
hay BD=4ID