Xét tam giác ABC , áp dụng tính chất phân giác trong tam giác , ta có:

\(\dfrac{AM}{MB}=\dfrac{AC}{CB}=\dfrac{AB}{CB}=\dfrac{AN}{NC}\left(=\dfrac{b}{a}\right)\)

Vậy MN // BC ( Định lí đảo của Thalès)

=> \(\dfrac{MN}{BC}=\dfrac{AM}{AB}=\dfrac{b}{b+a}\)( Định lý Thalès )

Vậy nên MN = \(\dfrac{ab}{a+b}\)

a) Xét tam giác ABC , áp dụng tính chất tia phân giác , ta có:

\(\dfrac{AD}{DB}\)= \(\dfrac{AC}{CB}\)=\(\dfrac{12}{6}\)=2

=> \(\dfrac{AD}{AB}\)= \(\dfrac{2}{3}\) =>AD=\(\dfrac{2}{3}\).12=8 (cm)

Do đó DB=12-8=4 (cm)

b) Do CE vuông góc với phân giác CD nên CE là phân giác ngoài tại đỉnh C của tam giác ABC

Vậy\(\dfrac{EB}{EA}\)=\(\dfrac{BC}{AC}\) hay \(\dfrac{EB}{EB+BA}\)=\(\dfrac{BC}{AC}\)

Gọi độ dài EB là x thì \(\dfrac{x}{x+12}\)=\(\dfrac{6}{12}\)

Vậy x = 12 (cm)

Xét $\Delta BED$ có {��//����=��{​MI//EDME=BM​ suy ra $ID=IB$.

Xét $\Delta CED$ có $\{$​NK//EDNC=ND​ suy ra $KE=KC$.

Suy ra ��=12��MI=\(\dfrac{1}{2}\)
​ED; ��=12��NK=\(\dfrac{1}{2}\)

​ED; ��=12��ED=\(\dfrac{1}{2}\)

​BC.

��=��−��=12��−12��=��−12��=12��IK=MK−MI=\(\dfrac{1}{2}\)
​BC−\(\dfrac{1}{2}\)
​DE=DE−\(\dfrac{1}{2}\)

​DE=\(\dfrac{1}{2}\)
​DE.

Vậy $MI=IK=KN$.

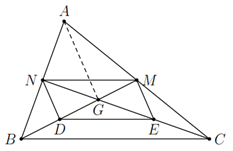
a) Vì $BM$, $CN$ là các đường trung tuyến của $\Delta ABC$ nên $MA=MC$, $NA=NB$.

Do đó $MN$ là đường trung bình của $\Delta ABC$, suy ra $MN$ // $BC$. (1)

Ta có $DE$ là đường trung bình của $\Delta GBC$ nên $DE$ // $BC$.  (2)

Từ (1) và (2) suy ra $MN$ // $DE$.

b) Xét $\Delta ABG$, ta có $ND$ là đường trung bình.

Xét $\Delta ACG$, ta có $ME$ là đường trung bình.

Do đó $ND$ // $AG$, $ME$ // $AG$.

Suy ra $ND$ // $ME$.

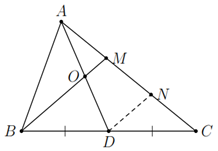
a) Qua $D$ vẽ một đường thẳng song song với $BM$ cắt $AC$ tại $N$.

Xét $\Delta MBC$ có $DB=DC$ và $DN$ // $BM$ nên ��=��=12��MN=NC=\(\dfrac{1}{2}\)

​MC (định lí đường trung bình của tam giác).

Mặt khác ��=12��AM=\(\dfrac{1}{2}\)
​MC, do đó ��=��=12��AM=\(\dfrac{1}{2}\)MN=
​MC.

Xét $\Delta AND$ có $AM=MN$ và $BM$ // $DN$ nên $OA=OD$ hay $O$ là trung điểm của $AD$.

b) Xét $\Delta AND$ có $OM$ là đường trung bình nên ��=12��OM=\(\dfrac{1}{2}\)

​DN. (1)

Xét $\Delta MBC$ có $DN$ là đường trung bình nên ��=12��DN=\(\dfrac{1}{2}\)​BM. (2)

Từ (1) và (2) suy ra ��=14��OM=\(\dfrac{1}{4}\)BM

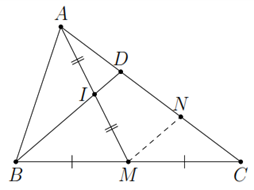
a) Kẻ MN // BD, N ∈ AC

MN là đường trung bình trong △ CBD

=> N là trung điểm của CD (1)

IN là đường trung bình trong △ AMN

=> D là trung điểm của AN (2)

Từ (1) và (2) => AD = \(\dfrac{1}{2}\)DC

b) Có ID = \(\dfrac{1}{2}\)MN ; MN = \(\dfrac{1}{2}\)BD , nên BD =ID 

Xét tam giác ABC có BC \(\perp\) AB' và B'C' \(\perp\) AB' nên BC // B'C'

Theo định lí Thalès, ta có \(\dfrac{AB}{AB'}=\dfrac{BC}{BC'}\)

=> \(\dfrac{x}{x+h}=\dfrac{a}{a'}\)

a'.x= a.(x+h)

a'.x - a.x= ah

x.(a'-a)= ah

x=\(\dfrac{ah}{a'-a}\)

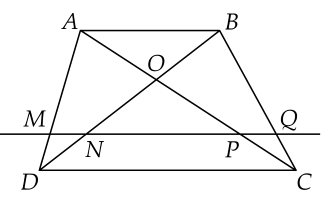
Trong tam giác ADB, ta có: MN // AB(gt)

=> \(\dfrac{DN}{DB}\)=\(\dfrac{MN}{AB}\)( hệ quả định lí thalès) (1)

Trong tam giác ACB , ta có PQ // AB(gt)

=> \(\dfrac{CQ}{CB}=\dfrac{PQ}{AB}\)(hệ quả của định  lý Thalès) (2)

Lại có : NQ // AB (gt); AB // CD (gt)

=> NQ // CD

Trong tam giác BDC , ta có NQ // CD (cmt)

=>\(\dfrac{DN}{DB}=\dfrac{CQ}{CB}\) ( định lí Thalès) (3)

Từ (1),(2),(3)=> \(\dfrac{MN}{AB}=\dfrac{PQ}{AB}\) hay MN= PQ(đpcm)

 Lấy D là trung điểm của BC

Khi đó AD là đường trung tuyến của tam giác ABC

Vì G là trọng tâm của tam giác ABC nên G nằm trên cạnh AD

Ta có :\(\dfrac{AG}{AD}\)=\(\dfrac{2}{3}\) hay AG= \(\dfrac{2}{3}\)AD

Vì MG // AB , theo định lí Thalès , ta có : \(\dfrac{AG}{AD}\)=\(\dfrac{BM}{BD}\)=\(\dfrac{2}{3}\)

Ta có : BD=CD(vì D là trung điểm của cạnh BC)nên \(\dfrac{DM}{BC}\)=\(\dfrac{DM}{2BD}\)=\(\dfrac{2}{2.3}\)=\(\dfrac{1}{3}\)

Do đó : BM=\(\dfrac{1}{3}\)BC(đpcm)

ABCD là hình thang =>AB // CD

Áp dụng hệ quả định lí Thalès, ta có:

\(\dfrac{OA}{OC}\)=\(\dfrac{OB}{OD}\)

=> OA.OD = OB.OC(đpcm)