a)

MAB

Vì điểm \(M\) là trung điểm của đoạn thẳng \(A B\).

Suy ra AM=MB=AB/2=42=2 (cm).

b) 

 Trường hợp 1.

MABxy

\(\hat{x M y} = 6 0^{\circ}\).

 Trường hợp 2.

MABxy

\(\hat{x M y} = 16 0^{\circ}\)

Số học sinh giỏi của lớp 6A là:

     \(\frac{7}{20} \cdot 40 = 14\) (học sinh) 

Số học sinh trung bình của lớp 6A là:

     \(\frac{1}{8} \cdot 40 = 5\) (học sinh) 

Số học sinh khá của lớp 6A là:

     \(14 + 5 = 19\) (học sinh) 

Số học sinh yếu của lớp 6A là:

     \(40 - \left(\right. 14 + 5 + 19 \left.\right) = 2\) (học sinh) .

a) \(\frac{1}{2} \cdot \frac{4}{3} - \frac{20}{3} \cdot \frac{4}{5}\)

\(= \frac{2}{3} - \frac{16}{3}\)

\(= - \frac{14}{3}\) ;

b) \(\frac{3}{7} + \frac{- 6}{19} + \frac{4}{7} + \frac{- 13}{19}\)

\(= \left(\right. \frac{3}{7} + \frac{4}{7} \left.\right) + \left(\right. \frac{- 6}{19} + \frac{- 13}{19} \left.\right)\)

\(= \frac{7}{7} + \frac{- 19}{19}\)

\(= 1 + \left(\right. - 1 \left.\right) = 0\) ;

c) \(\frac{3}{5} \cdot \frac{8}{9} - \frac{7}{9} \cdot \frac{3}{5} + \frac{3}{5} \cdot \frac{26}{9}\)

\(= \frac{3}{5} \cdot \left(\right. \frac{8}{9} - \frac{7}{9} + \frac{26}{9} \left.\right)\)

\(= \frac{3}{5} \cdot \frac{27}{9}\)

\(= \frac{3}{5} \cdot 3\)

\(= \frac{9}{5}\).

1)

a) Có \(3\) kết quả khác nhau trong mỗi lần lấy bóng là:

- Hòa lấy ra quả bóng đỏ (kí hiệu: Đ).

- Hòa lấy ra quả bóng xanh (kí hiệu: X).

- Hòa lấy ra quả bóng vàng (kí hiệu: V).

b) Hai điều chú ý của mô hình xác suất là:

- Hòa lấy ra ngẫu nhiên một quả bóng trong hộp.

- Tập hợp các kết quả có thể xảy ra là: {Đ, X, V}. Các kí hiệu được giải thích ở phần trên.

c) Trong \(9\) lần lấy ngẫu nhiên, có \(4\) lần bạn Hòa lấy ra quả bóng màu Xanh.

Xác suất thực nghiệm của kết quả bạn Hòa lấy ra quả bóng màu Xanh là:

\(4 : 9 = \frac{4}{9}\)

1)

a) Tập hợp các điểm thuộc đoạn thẳng \(B D\) là \(B ; C ; D\), tập hợp các điểm thuộc không đoạn thẳng \(B D\) là \(A ; E\).

b) Cặp đường thẳng song song là \(A B\) // \(D E\).

c) Gợi ý: Liệt kê theo các giao điểm, có 5 giao điểm nên có 5 cặp đường thẳng cắt nhau.

Các cặp đường thẳng cắt nhau là

\(A B\) và \(A E\) cắt nhau tại \(A\).

\(B A\) và \(B D\) cắt nhau tại \(B\).

\(A E\) và \(B D\) cắt nhau tại \(C\).

\(D E\) và \(D B\) cắt nhau tại \(D\).

\(E A\) và \(E D\) cắt nhau tại \(E\).

2) 

a) 

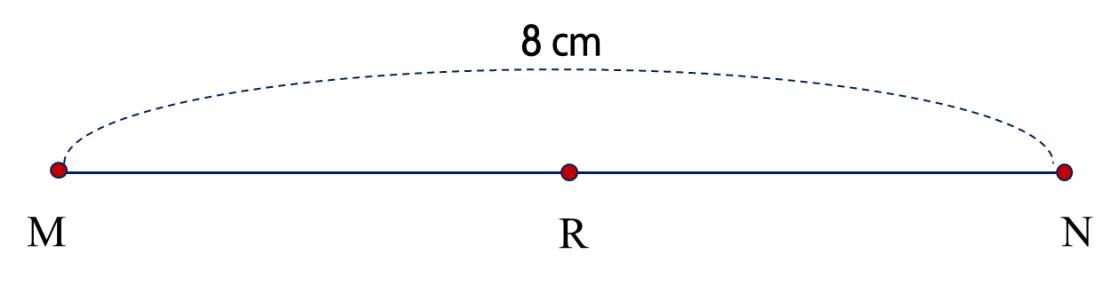
Vì \(R\) là trung điểm của đoạn thẳng \(M N\), nên ta có \(M R = R N = M N : 2\).

Độ dài của đoạn thẳng \(M R\) hay \(R N\) là:

\(8 : 2 = 4\) (cm)

b)

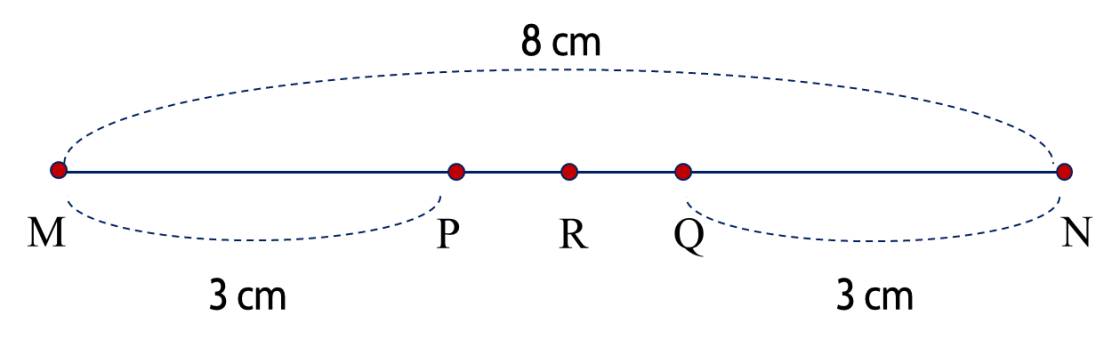
Nhìn hình vẽ, ta thấy \(R\) nằm giữa \(P\) và \(Q\); \(M N = M P + P Q + Q N\); \(M R = M P + P R\).

Độ dài của đoạn thẳng \(P Q\) là

\(8 - 3 - 3 = 2\) (cm).

Độ dài của đoạn thẳng \(P R\) là

\(4 - 3 = 1\) (cm).

Từ đây, ta thấy \(P R : P Q = \frac{1}{2}\),

Vậy \(R\) là trung điểm \(P Q\).

3)

Chọn 1 điểm nối với \(11\) điểm còn lại ta được \(11\) đường thẳng, làm như thế với \(12\) điểm ta được \(12. \left(\right. 12 - 1 \left.\right) = 132\) đường thẳng. Nhưng mỗi đường thẳng lặp lại \(2\) lần nên số đường thẳng vẽ được là \(132 : 2 = 66\) đường thẳng.

Qua \(4\) điểm không thẳng hàng sẽ vẽ được \(6\) đường thẳng.

Qua \(4\) điểm thẳng hàng vẽ được \(1\) đường thẳng nên số đường thẳng giảm đi \(5\) đường thẳng

Vậy số đường thẳng vẽ được là \(66 - 5 = 61\) đường thẳng vậy ta vẽ được 61 đường thẳng.

+ \(S = \frac{1}{31} + \frac{1}{32} + \frac{1}{33} + \ldots + \frac{1}{60}\)

\(S < \left(\right. \frac{1}{30} + \frac{1}{30} + \ldots + \frac{1}{30} \left.\right) + \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right)\)

\(S < \frac{10}{30} + \frac{10}{40} + \frac{10}{50} < \frac{48}{60} = \frac{4}{5} ;\)

+ \(S > \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right) + \left(\right. \frac{1}{60} + \frac{1}{60} + \ldots + \frac{1}{60} \left.\right)\)

\(S > \frac{10}{40} + \frac{10}{50} + \frac{10}{60} > \frac{3}{5} .\)

a) Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

\(15\) quả; \(20\) quả; \(10\) quả.

b) Cả ba tháng cửa hàng bán được:

\(15 + 20 + 10 = 45\) (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

\(20 – 10 = 10\) (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

\(3 : 4 = \frac{3}{4}\)

1. a) \(O\) thuộc các đoạn thẳng: \(AB;CD;OA;OB;OC;OD.\)

b) Ta có \(O\) nằm giữa hai điểm \(A\) và \(B\) và \(OA=OB=3\) cm nên \(O\) là trung điểm của đoạn thẳng \(A B .\)

2. a) Số đo góc \(x O y\) bằng \(3 0^{\circ}\).

b)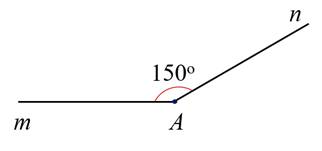 

a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)

\(= 1 + \left(\right. - 1 \left.\right)\)

= 0

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)

\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)

\(= \frac{17}{8} : \frac{49}{8}\)

\(= \frac{17}{49}\).

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)

\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)

\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)

\(= \frac{1}{5} + \frac{4}{5} = 1.\)

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)

1.a) lập bảng

2.a

2.b) đối tượng thống kê là số điểm từ 5 đến 8

Tiêu chí thông kê là số người có được điểm đó