tam giác ABC cân tại A nên

 \(\widehat{B}\) = \(\widehat{C}\) 

=> \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)

AB = AC (2)

\(\widehat{BAM}\) = \(\widehat{CAN}\) = 90⁰ (3)

Kết hợp (1); (2); (3)  ta có : Δ BAM = Δ CAN ( g-c-g)

=> BM = CN 

BM = BN + MN = MN + CM

⇒ BN = CM

\(\widehat{BAN}\)  + \(\widehat{NAC}\) = \(\widehat{BAC}\) = 120⁰

⇒ \(\widehat{BAN}\) = 120⁰ - \(\overline{NAC}\) = 120⁰ - 90⁰ = 30⁰

\(\widehat{ABN}\) =  ( 180⁰ - 120 ⁰ ) : 2 = 30⁰  = \(\widehat{BAN}\) ⇒Δ ANB cân tại N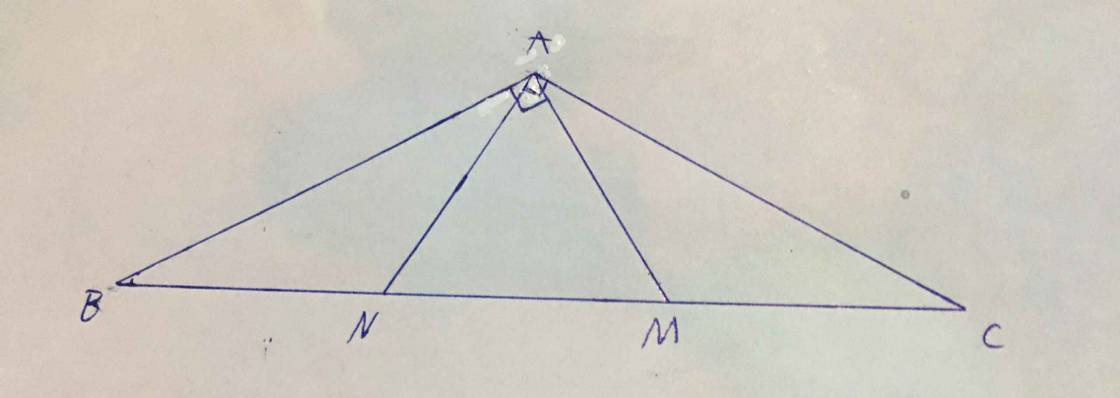 

a, \(\dfrac{x}{-3}\)= \(\dfrac{7}{4}\) ⇒ x = \(\dfrac{7}{4}\)x (-3) ⇒ x = - \(\dfrac{21}{4}\)

b, \(\dfrac{x+9}{15-x}\) = \(\dfrac{2}{3}\)  ⇒ 3(x+9)  = 2( 15-x) ⇒ 3x + 27 = 30 - 2x

⇒ 3x + 2x = 30 - 27 ⇒

 5x = 3 ⇒ x = 3 : 5 ⇒ x = \(\dfrac{3}{5}\)

                    x³  - 3x² +  x + 1

              ^-   2x³ -   x² + 3x - 4

              _________________

               -x³  -  2x² - 2x + 5 

P(x) - Q(x) = -x³ - 2x² - 2x + 5

b, Thay x = 1 vào P(x); Q(x) ta có : 

P(1) = 1³ - 3.1² + 1 + 1 = 0  

Q(1) = 2.1³ - 1² + 3.1 - 4 = 0

Vậy 1 là nghiệm của cả hai đa thức P(x) và Q(x)

a, Thể tích bể : 1,5 x 1 x 0,9 = 1,35 (m³)

b, Thể tích nước trong bể : 1,5 x 1 x 0,5 = 0,75 (m³)

c, Thể tích nước trong bể sau khi thả hòn đá :

1,5 x 1 x ( 0,5 + 0,2) = 1,05 (m³)

Thể tích hòn đá :

1,05 - 0,75 = 0,3 (m³)

Đs...

1, Cạnh hình vuông : 24 : 4 = 6 (cm)

Diện tích : 6 x 6 = 36 (cm²)

2, vì 16 = 4 x 4 

Cạnh hình vuông 4 cm

Chu vi hình vuông 4 x 4 = 16 (cm)

3, Nửa chu vi : 40 : 2 = 20 (cm)

Chiều dài : 20 - 8 = 12 (cm)

Diện tích : 12 x 8 = 96 (cm²)

4, Chiều rộng 36 : 9 = 4 (cm)

Chu vi : ( 9 + 4) x 2 = 26 (cm)

5,Nửa  Chu vi hình vuông 8 x 2 = 16 (cm)

Nửa Chu vi hình chữ nhật là 16 cm

Chiều rộng 16 - 10 = 6 (cm)

Diện tích hình chữ nhật : 10 x 6 = 60 (cm²)

Gọi chiều dài là x, chiều rộng là y ( x,y > 0)

Nửa chu vi hình chữ nhật là 60 : 2 = 30 (cm)

Theo bài ra ta có: \(\dfrac{x}{y}\) = \(\dfrac{2}{3}\) ⇒ \(\dfrac{x}{2}\) = \(\dfrac{y}{3}\) 

Áp dụng tính chất dãy tỉ số bằng nhau ta có : 

\(\dfrac{x}{2}\) = \(\dfrac{y}{3}\) = \(\dfrac{x+y}{2+3}\) = \(\dfrac{30}{5}\) = 6

x = 6.2 = 12

y = 6.3 = 18

Diện tích hình chữ nhật : 18 x 12 = 216 (m²)

Kết luận : diện tích hình chữ nhật 216 m²

Thời gian người đó đi và về là:

3 giờ 40 phút - 10 phút = 3 giờ 30 phút 

3 giờ 30 phút = 3,5 giờ

Gọi quãng đường AB là x ( x > 0)

Theo bài ra ta có : \(\dfrac{x}{40}+\dfrac{x}{30}\) = 3,5

                             x( \(\dfrac{1}{40}+\dfrac{1}{30}\)) = 3,5

                           x = 3,5 : ( \(\dfrac{1}{40}+\dfrac{1}{30}\))

                          x = 60 

Quãng đường AB là 60 km 

\(\dfrac{4}{7}\) của ( - 1260 ) là:

- 1260 x  \(\dfrac{4}{7}\) = - 720

\(\dfrac{5}{9}\) của một số là - 720 

Số đó là : - 720 : \(\dfrac{5}{9}\) = - 1296

Gọi số máy cày của đội 1, đội 2, đội 3 lần lượt là : x, y, z (x,y,z \(\in\)N)

Theo bài ra ta có : 5x = 6y = 8z

                               6y = 8z => \(\dfrac{y}{8}\) = \(\dfrac{z}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

                                 \(\dfrac{y}{8}\) = \(\dfrac{z}{6}\) = \(\dfrac{y-z}{8-6}\) = \(\dfrac{5}{2}\)

                                  y = \(\dfrac{5}{2}\) x 8 = 20

                                  z = \(\dfrac{5}{2}\) x 6 = 15

                                 x = 6 x 20 : 5 = 24

Kết luận : Số máy cày của đội 1, đội 2, đội 3 lần lượt là  24 máy; 20 máy; 15 máy. 

Vì tổng hai số lớn nhất và bé nhất được lập từ 4 chữ số là 1241 

mà 9 + 2 = 11;  8 + 3 = 11; 7 + 4 = 11; 6 + 5 = 11; 0 + 1 = 1

Vì đấy là tổng của số lớn nhất và số bé nhất được lập từ 4 chữ số nên nhất định phải có chữ số hàng đơn vị lớn nhất và bé nhất có thể. vậy 2 chữ số trong 4 chữ số đó là 9; 2 

9 + 2 = 11

14 - 1 = 13

13 = 9 + 4 = 8 + 5 = 7 + 6 => 2 số còn lại 8;5 hoặc 7; 6

Ta có 9852 + 2589 = 12441 ( thỏa mãn)

        9762 + 2679 = 12441 ( thỏa mãn)

 9 + 8 + 5 + 2 = 24 

 9 + 7 + 6 + 2 = 24 

Kết luận a + b + c + d = 24