

Nguyễn Thị Thương Hoài
Giới thiệu về bản thân



































S4 = 12 + 22 + 32 +...+ 1002
S4 = 1 + 2.2 + 3.3+...+100.100
S4 = 1 + 2.(1+1) + 3.( 2+1) +...+ 100.(99+1)
S4 = 1 + 1.2 + 2 + 2.3 + 3 +...+ 99.100 + 100
S4 = (1 + 2 + 3 +...+ 100) + ( 1.2 + 2.3 + ...+ 99.100)
Đặt A = 1 + 2 + 3 +...+ 100; B = 1.2 + 2.3 +...+ 99.100
A = 1 + 2 + 3 +...+ 100
Xét dãy số 1; 2; 3; ...; 100, dãy số trên là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là: (100 - 1):1 + 1 = 100
Tổng A là: A = (100 +1).100 : 2 = 5050
B = 1.2 + 2.3 + 3.4 +...+ 99.100
3B = 1.2.3 + 2.3.3 + 3.4.3 +...+ 99.100.3
1.2.3 = 1.2.3
2.3.3 = 2.3.(4-1) = 2.3.4 - 1.2.3
3.4.3 = 3.4.(5-2) = 3.4.5 - 2.3.4
...................................................
99.100.3 = 99.100.(101 - 98) = 99.100.101- 98.99.100
Cộng vế với vế ta có:
3B = 99.100.101
B = 99.100.101: 3
B = 333300
S4 = 5050 + 333300 = 338350
1 + 2 + 3 +...+ \(x\) = \(\overline{aaa}\)
Đặt 1 + 2 + 3 +...+ \(x\) = B
xét dãy số
1; 2; 3; ...; \(x\)
Dãy số trên là dãy số cách đều với khoảng cách là: 2 - 1 = 1
Dãy số trên có số số hạng là: (\(x\) - 1): 1 + 1 = \(x\)
Tổng B = ( \(x\) + 1) \(\times\) \(x\) : 2 = \(\overline{aaa}\)
(\(x\) + 1) \(\times\) \(x\) = \(\overline{aaa}\) \(\times\) 2
(\(x\) + 1) \(\times\) \(x\) = 2 \(\times\) 111 \(\times\) a
(\(x\) + 1) \(\times\) \(x\) = 2 \(\times\) 3 \(\times\) 37 \(\times\) a
(\(x\) + 1)\(\times\) \(x\) = 37\(\times\)6\(\times\)a = 74\(\times\)3\(\times\)a = 111 \(\times\) 2 \(\times\) a
⇒ 6 \(\times\) a = 36; 38; 3 \(\times\) a = 73; 75; 2 \(\times\) a = 110; 112
Lập bảng ta có:
| 6 \(\times\) a | 36 | 38 |
| a | 6 | \(\dfrac{19}{3}\)(loại) |
| 3 \(\times\) a | 73 | 75 |
| a | \(\dfrac{73}{3}\) (loại) | \(\dfrac{75}{3}\) (loại) |
| 2 \(\times\) a | 110 | 112 |
| a | 55 (loại) | 56 (loại) |
Vậy a = 6 ⇒ (\(x\) + 1) \(\times\) \(x\) = 37 \(\times\) 36 ⇒ \(x\) = 36
Đáp số \(x\) = 36; a = 6
-1 + 0,35
= -( 0,65 + 0,35) + 0,35
= - 0,65 - 0,35 + 0,35
= - 0,65 - (0,35 - 0,35)
= - 0,65 - 0
= -0,65 (đpcm)
Đpcm
M = 2050 \(\times\) 2052 = (2051 -1)\(\times\) 2052 = 2051 \(\times\) 2052 - 2052
N = 2051 \(\times\) 2051 = 2051 \(\times\) (2052 - 1) = 2051 \(\times\) 2052 - 2051
Vì 2052 > 2051 nên 2051\(\times\) 2052 - 2052 < 2051 \(\times\)2052 - 2051
vậy M < N
\(\dfrac{1}{4}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{24}\) + \(\dfrac{1}{40}\) + \(\dfrac{1}{60}\) + \(\dfrac{1}{84}\) + \(x\) = 1
\(\dfrac{1}{2.2}\) + \(\dfrac{1}{2.6}\)+\(\dfrac{1}{2.12}\)+\(\dfrac{1}{2.20}\) + \(\dfrac{1}{2.30}\) + \(\dfrac{1}{2.42}\) + \(x\) =1
\(\dfrac{1}{2}\).(\(\dfrac{1}{2}\) + \(\dfrac{1}{6}\)+\(\dfrac{1}{12}\)+\(\dfrac{1}{20}\) + \(\dfrac{1}{30}\)+ \(\dfrac{1}{42}\)) + \(x\) = 1
\(\dfrac{1}{2}\).( \(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\)+ \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\)) + \(x\) = 1
\(\dfrac{1}{2}\).( \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)) + \(x\) = 1
\(\dfrac{1}{2}\).( \(\dfrac{1}{1}\) - \(\dfrac{1}{7}\)) + \(x\) = 1
\(\dfrac{1}{2}\).\(\dfrac{6}{7}\) + \(x\) = 1
\(\dfrac{3}{7}\) + \(x\) = 1
\(x\) = 1 - \(\dfrac{3}{7}\)
\(x\) = \(\dfrac{4}{7}\)
M = 2050 \(\times\) 2052 = 2050 \(\times\) (2051+ 1) = 2050 \(\times\) 2051 + 2050
N = 2051\(\times\) 2051 = (2050 + 1)\(\times\) 2051 = 2050 \(\times\) 2051 + 2051
Vì 2050 < 2051 nên 2050 \(\times\) 2051 + 2050 < 2050 \(\times\) 2051 + 2051
Vậy M < N
Trong phạm vi tiểu học thì em sẽ được học:
Phân số gồm tử số và mẫu số trong đó tử số và mẫu số là các số tự nhiên và mẫu số khác không, tử số được viết trên dấu gạch ngang và mẫu số được viết dưới dấu gạch ngang
Kiến thức cần nhớ: Trung bình cộng của ba số tự nhiên liên tiếp bằng số thứ hai
Giải
Số thứ hai là: 444 : 3 = 148
Số thứ nhất là: 148 - 1 = 147
Số thứ ba là: 148 + 1 = 149
Trong ba số tự nhiên liên tiếp có tổng bằng 444 thì có 2 số là số lẻ và 1 số là số chẵn. Ba số đó lần lượt là: 147; 148; 149
Bài 1: Ta có sơ đồ
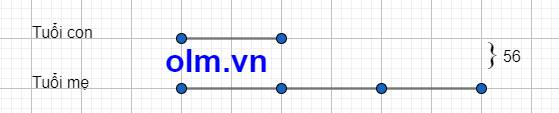
Theo sơ đồ ta có: Tuổi con hiện nay là: 56:(1+3) = 14 (tuổi)
Tuổi mẹ hiện nay là: 56 - 14 = 42 (tuổi)
Hiện nay, Mẹ hơn con: 42 - 14 = 28 (tuổi)
Hiệu số tuổi luôn không thay đổi theo thời gian, nên khi mẹ gấp hai lần tuổi con thì mẹ vẫn hơn con 28 tuổi
Ta có sơ đồ:

Theo sơ đồ ta có:
Tuổi con khi mẹ gấp 2 lần tuổi con là: 28:(2-1) = 28 (tuổi)
Mẹ sẽ gấp 2 lần tuổi con sau: 28 - 14 = 14(năm)
Đáp số: tuổi con hiện nay là 14 tuổi
tuổi mẹ hiện nay là 42 tuổi
mẹ gấp 2 lần tuổi con sau 14 năm nữa.
Bài 2: Tổng của hai số là: 120 \(\times\) 2 = 240
Tỉ số của số thứ nhất và số thứ hai là: \(\dfrac{1}{7}\) : \(\dfrac{1}{3}\) = \(\dfrac{3}{7}\)
Ta có sơ đồ:

Theo sơ đồ ta có: Số thứ nhất là: 240 : (3 + 7)\(\times\) 3 = 72
Số thứ hai là: 240 - 72 = 168
Đáp số: Số thứ nhất 72; số thứ hai 168