Gọi \(s\) là quãng đường viên đá đi được sau khoảng thời gian \(t\) kể từ khi bắt đầu rơi tới khi chạm đất

\(s_{1}\) là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian \(t_{1} = t - 1\)

Ta có: \(s = \frac{1}{2} g t^{2}\) và \(s_{1} = \frac{1}{2} g \left(\left(\right. t - 1 \left.\right)\right)^{2}\)

Quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:

\(\Delta s = s - s_{1} = \frac{1}{2} g t^{2} - \frac{1}{2} g \left(\left(\right. t - 1 \left.\right)\right)^{2} = g t - \frac{1}{2} g\)

\(\Rightarrow t = \frac{\Delta s}{g} + \frac{1}{2} = \frac{14 , 7}{9 , 8} + \frac{1}{2} = 2\) s

a. Vẽ đồ thị độ dịch chuyển – thời gian của Nam.

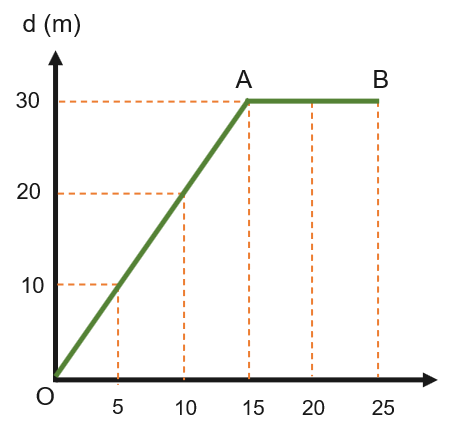
b. Mô tả chuyển động của Nam:

- Từ 0 – 15 giây: Nam chuyển động thẳng đều với vận tốc: \(\text{v}_{1} = \frac{\Delta d_{1}}{\Delta t_{1}} = \frac{30}{15} = 2\) m/s

- Từ giây thứ 15 đến giây thứ 25: Nam đứng yên (dừng lại).

c. Vận tốc của Nam trong 15 s đầu là:

\(\text{v}_{1} = \frac{\Delta d_{1}}{\Delta t_{1}} = \frac{30}{15} = 2\) m/s

Vận tốc của Nam trong suốt quá trình chuyển động:

\(\text{v} = \frac{\Delta d}{\Delta t} = \frac{30}{25} = 1 , 2\) m/s

Chọn chiều dương là chiều chuyển động của ô tô, gốc thời gian lúc bắt đầu hãm phanh.

Đổi 64,8 km/h = 18 m/s; 54 km/h = 15 m/s; 36 km/h = 10 m/s

a. Gia tốc của ô tô:

\(a = \frac{\text{v}_{1} - \text{v}_{0}}{\Delta t} = \frac{15 - 18}{10} = - 0 , 3\) m/s²

Thời gian kể từ khi hãm phanh đến khi ô tô đạt vận tốc v₂ = 36 km/h = 10 m/s là:

\(\text{v} = \text{v}_{0} + a t \Rightarrow t = \frac{\text{v}_{2} - \text{v}_{0}}{a} = \frac{10 - 18}{- 0 , 3} = 26 , 7\) s

b. Thời gian kể từ khi hãm phanh đến khi ô tô dừng hẳn \(\text{v}_{3} = 0\) là:

\(t^{'} = \frac{\text{v}_{3} - \text{v}_{0}}{a} = \frac{0 - 18}{- 0 , 3} = 60\) s

c. Ta có: \(\text{v}_{2}^{2} - \text{v}_{0}^{2} = 2 a s\)

Vậy quãng đường ô tô đi được đến khi dừng hẳn là:

s=2av32​−v02​​=2(−0,3)0−182​=540 m

Ta có: \(\text{v}_{0} = 5.1 0^{5}\) m/s; \(\text{v} = 5 , 4.1 0^{5}\) m/s; \(a = 8.1 0^{4}\) m/s²

Thời gian electron bay được trong khi được gia tốc là:

\(t = \frac{\text{v} - \text{v}_{0}}{a} = \frac{5 , 4.1 0^{5} - 5.1 0^{5}}{8.1 0^{4}} = 0 , 5 s\)

Quãng đường electron bay được trong khi được gia tốc là:

\(s = \frac{\text{v}^{2} - \text{v}_{0}^{2}}{2 a} = \frac{\left(\left(\right. 5 , 4.1 0^{5} \left.\right)\right)^{2} - \left(\left(\right. 5.1 0^{5} \left.\right)\right)^{2}}{2.8.1 0^{4}} = 26.1 0^{4} m\)

a. Độ cao của nơi thả viên bi so với mặt đất là:

\(h = \frac{1}{2} g t^{2} = \frac{1}{2} . 9 , 8. 3^{2} = 44 , 1\) m

b. Vận tốc lúc chạm đất là:

\(\text{v} = g t = 9 , 8.3 = 29 , 4\) m/s

c. Quãng đường vật rơi trong 2,5 s đầu là:

\(s_{1} = \frac{1}{2} g t_{1}^{2} = \frac{1}{2} . 9 , 8.2 , 5^{2} = 30 , 625\) m

Quãng đường vật rơi trong 0,5 s cuối là:

\(s = h - s_{1} = 44 , 1 - 30 , 625 = 13 , 475\) m

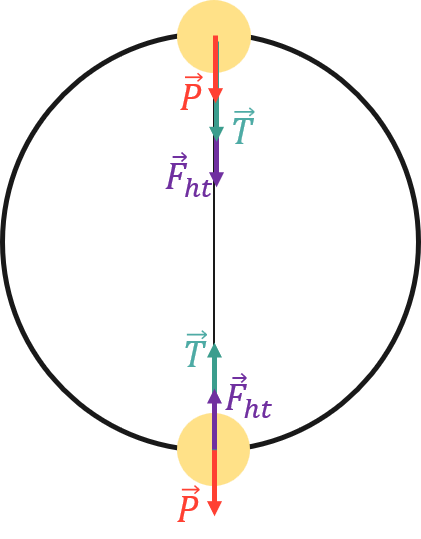
Hợp lực của lực căng dây \(T\) và trọng lực \(P\) đóng vai trò lực hướng tâm.

Ta có: \(\left(\overset{\rightarrow}{F}\right)_{h t} = \overset{\rightarrow}{P} + \overset{\rightarrow}{T}\)

Chọn hệ quy chiếu gắn với mặt đất, chiều dương hướng xuống.

Ở điểm cao nhất của quỹ đạo: \(F_{h t} = P + T\)

\(\Rightarrow T = m \omega^{2} r - m g = 0 , 3. 8^{2} . 0 , 5 - 0 , 3.10 = 6 , 6 N\)

Ở điểm thấp nhất của quỹ đạo: \(F_{h t} = T - P\)

\(\Rightarrow T = m \omega^{2} r + m g = 0 , 3. 8^{2} . 0 , 5 + 0 , 3.10 = 12 , 6 N\)

a. Áp suất xe tăng tác dụng lên mặt đường:

\(p_{1} = \frac{F_{1}}{S_{1}} = \frac{P_{1}}{S_{1}} = \frac{m_{1} g}{S_{1}} = \frac{2600.10}{1 , 3} = 20000\) N/m²

b. Áp suất của người tác dụng lên mặt đường:

\(p_{2} = \frac{F_{2}}{S_{2}} = \frac{P_{2}}{S_{2}} = \frac{m_{2} g}{S_{2}} = \frac{45.10}{200.1 0^{- 4}} = 22500\) N/m²

Áp suất của người tác dụng lên mặt đường là lớn hơn áp suất của xe tăng tác dụng lên mặt đường.

Coi hệ gồm người và xe là một hệ kín.

Theo định luật bảo toàn động lượng ta có: \(m_{1} \left(\overset{\rightarrow}{\text{v}}\right)_{1} + m_{2} \left(\overset{\rightarrow}{\text{v}}\right)_{2} = \left(\right. m_{1} + m_{2} \left.\right) \overset{\rightarrow}{\text{v}^{'}}\)

Chọn chiều dương là chiều chuyển động của xe.

a. Trường hợp hòn đá bay theo phương ngang, ngược chiều xe với vận tốc \(\text{v}_{2} = 12\) m/s, áp dụng định luật bảo toàn động lượng của hệ theo phương ngang ta có:

\(m_{1} \text{v}_{1} + m_{2} \text{v}_{2} = \left(\right. m_{1} + m_{2} \left.\right) \text{v}^{'}\)

\(\Rightarrow \text{v}^{'} = \frac{m_{1} \text{v}_{1} + m_{2} \text{v}_{2}}{m_{1} + m_{2}} = \frac{300.10 + 0 , 5. \left(\right. - 12 \left.\right)}{300 + 0 , 5} = 9 , 96\) m/s

b. Trường hợp hòn đá rơi theo phương thẳng đứng, áp dụng định luật bảo toàn động lượng của hệ theo phương ngang ta có:

\(m_{1} \text{v}_{1} = \left(\right. m_{1} + m_{2} \left.\right) \text{v}\)

\(\Rightarrow \text{v} = \frac{m_{1} \text{v}_{1}}{m_{1} + m_{2}} = \frac{300.10}{300 + 0 , 5} = 9 , 98\) m/s

a,I=0.16 A

b,F=4.10-⁴

a,Công suất hao phí trên đường dây là P=40kW

Hiệu suất truyền tải là H=20%

Độ giảm thế trên đường dây: ΔU=400 V

Hiệu điện thế tại nơi tiêu thụ điện là U'=100V

 b,Công suất hao phí trên đường dây khi đó là P'=400w

Hiệu suất truyền tải là H=99,2%

Độ giảm thế trên đường dây:ΔU=40V

Hiệu điện thế tại nơi tiêu thụ điện là U'=4960 V