

Trần Đinh Nguyễn
Giới thiệu về bản thân



































a) Dấu hiệu vi phạm pháp luật và hành vi vi phạm pháp luật của anh T : Điều khiển xe mô tô đi ngược chiều trên đường cao tốc
b) Trách nhiệm pháp lí của anh T : nộp tiền xử phạt vi phạm hành chính và chấp hành theo điều, khoản quy định của Luật Giao thông đường bộ
- Xây dựng kế hoạch chi tiêu phù hợp với bản thân, gia đình
- Tìm hiểu thông tin về sản phẩm trước khi mua
- Sử dụng sản phẩm an toàn, hiệu quả
- Xác định phương thức thanh thức phù hợp
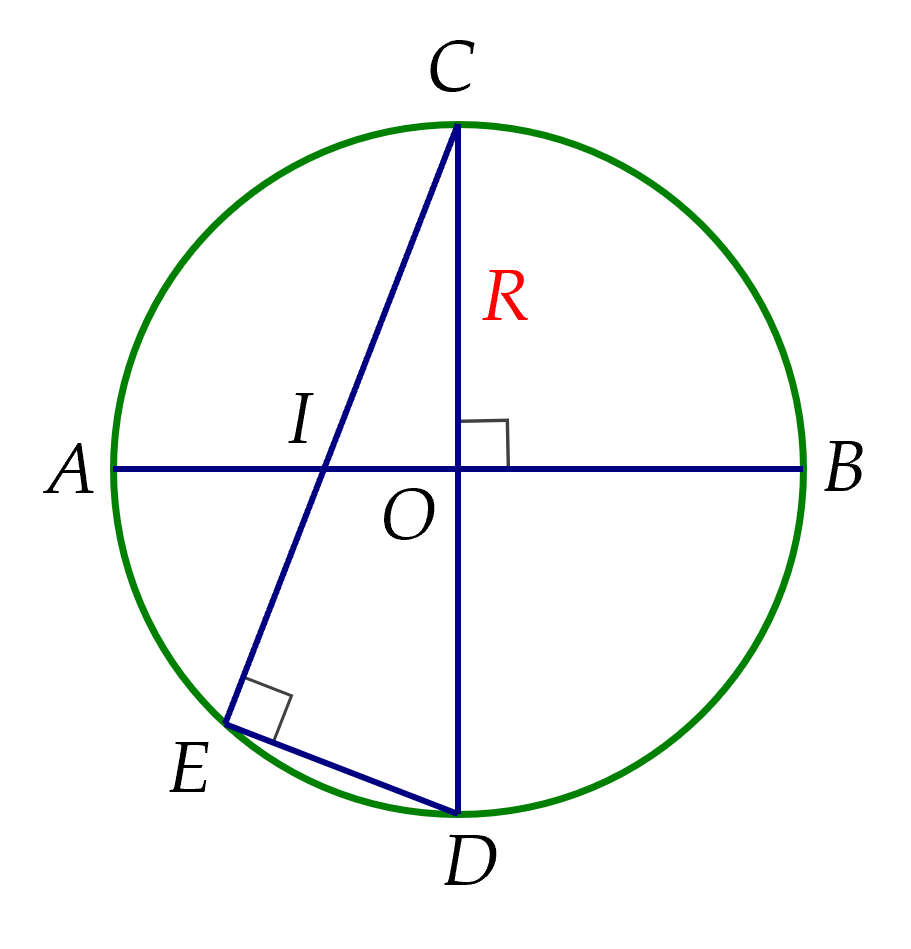
Hướng dẫn giải:
a) Gọi E,FE,F là tiếp điểm của đường tròn (I)(I) với các cạnh AB,ACAB,AC
Theo tính chất của hai tiếp tuyến cắt nhau, ta có: AE=AF;BE=BD;CD=CFAE=AF;BE=BD;CD=CF
Do đó: 2BD=BD+BE=BC−CD+AB−AE2BD=BD+BE=BC−CD+AB−AE
=BC+AB−(CD+AE)=BC+AB−(CF+AF)=BC+AB−(CD+AE)=BC+AB−(CF+AF)
=BC+AB−AC suy ra BD=BC+AB−AC2BD=(BC-AB+AC)=2
ta có: DC=BC+AC−AB2DC=(BC+AC−AB)/2 mà AB2+AC2=BC2AB2+AC2=BC2 (ΔABCΔABC vuông tại AA), do đó:
BD.DC=(BC+AB−AC)(BC+AC−AB)/2
BC2
−(AB−AC)2
/4=BC
2−AB2
−AC2
+2AB.AC/4
=AB.AC/2 =SABC
Áp dụng định lý pythagore vào △ ABC vuông tại A:
Có BC2 =AB2 + AC2=92 + 122=225
⇒BC=♪225=15 cm
Áp dụng công thức tính bán kính vào trong bài, ta được:
r=(2AB+AC−BC)/2=(9+12−15)/2=6/2=3 cm
Ta có công thức:IG=3/1×độ dài của cạnh huyền (BC)
Với cạnh huyền BC = 15 \, \text{cm}BC=15cm, ta có:
IG=13×BC=13×15=5 cmIG = \frac{1}{3} \times BC = \frac{1}{3} \times 15 = 5 \, \text{cm}Vậy độ dài đoạn IG là 5 cm
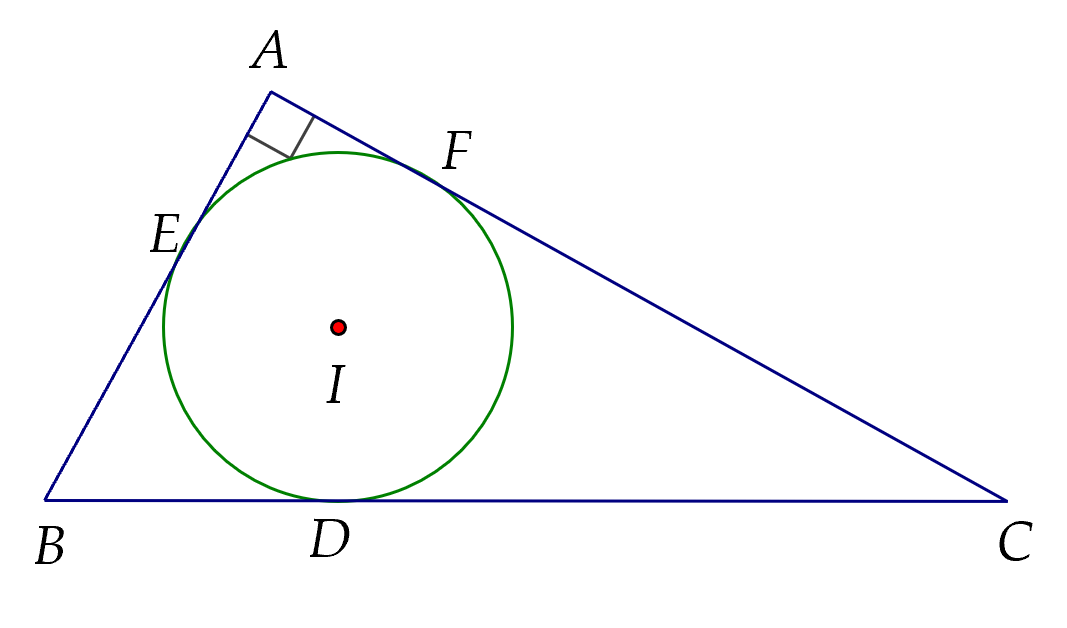
Đường tròn (I;r)(I;r) tiếp xúc với các cạnh AB,AC,BCAB,AC,BC theo thứ tự M,N,PM,N,P.
Ta có: SAIB=12IM.AB=12r.ABSAIB=21IM.AB=21r.AB (1);
SAIC=12IN.AC=12r.ACSAIC=21IN.AC=21r.AC (2);
SBIC=12r.BCSBIC=21r.BC (3)
Cộng vế theo vế của (1), (2) và (3), ta được: SAIB+SAIC+SBICSABC=12r.(AB+AC+BC)SABCSAIB+SAIC+SBIC=21r.(AB+AC+BC)
Mà SABC=12AB.AC=6.82=24SABC=21AB.AC=26.8=24 cm2, BC=62+82=100=10BC=62+82=100=10 cm
Nên ta có: 24=12r(6+8+10)24=21r(6+8+10) suy ra r=2r=2 (cm).
(chú thích câu sau:☹ là kí hiệu căn bậc hai)
Nối và . Kẻ ().
Sau giờ tàu chạy được quãng đường là: (hải lí).
Sau giờ tàu chạy được quãng đường là: (hải lí).
Xét tam giác vuông tại , ta có:
CH=AC*sin A = 22,5*sin 60=45☹3/4(hải lí)
AH=AC.cosA=22,5.cos60=11,25(hải lí)
Do đó (hải lí).
Mặt khác, tam giác vuông tại , áp dụng định lí Pythagore ta có: BC=☹BH2 +CH2 =☹(18,75)2+(45☹3/4)2 ≈ 27,04(hải lí) Vậy sau 1,5 giờ tàu B cách tàu C là 27,04 hải líGọi x,y lần lượt là giá niêm yết của mặt hàng A và B (x,y>0)
Trong đợt khuyến mại, mặt hàng A được giảm giá 20% và mặt hàng B được giảm giá 15% so với giá niêm yết.Một khách hàng mua hai món hàng A và hai món hàng B phải trả số tiền là 362000 đồng
⇒Ta có phương trình:0,80x*2+0,85y=362000(I)
Nếu mua trong khung giờ vàng thì món hàng A được giảm giá 30% so với giá niêm yết hay 0,70x
Nếu mua trong khung giờ vàng thì món hàng B được giảm giá 25% so với giá niêm yết hay 0,75y
Một khách hàng mua ba món hàng A và hai món hàng B trong khung giờ vàng nên phải trả số tiền là 552000 đồng
⇒Ta có phương trình:0,70x*3+0,75y*2=552000(II)
Từ (I) và (II) , ta có hệ phương trình:
{0,8x*2+0,85y=362000
{0,7x*3+0,75y*2=552000
{1,6x+0,85y=362000(1)
{2,1x+1,5y=552000(2)
Nhân cả hai vế của phương trình (1) cho 1,5, ta có:2,4x+1,275=543000(3)
Nhân cả hai vế của phương trình (2) cho 1,85,ta có:1,785x+1,275=469200(4)
Trừ từng vế của phương trình (3) cho phương trình (4), ta được:
0,615x=73800
x=120000(tmđk)
Thay x=120000 vào phương trình (2), ta được:
2,1*120000+1,5y=552000
252000+1,5y=552000
1,5y=552000-252000
1,5y=300000
y=200000
Vậy mặt hàng A có giá tiền là 120000 đồng và mặt hàng B có giá tiền là 200000 đồng
Gọi x,y lần lượt là giá niêm yết của mặt hàng A và B (x,y>0)
Trong đợt khuyến mại, mặt hàng A được giảm giá 20% và mặt hàng B được giảm giá 15% so với giá niêm yết.Một khách hàng mua hai món hàng A và hai món hàng B phải trả số tiền là 362000 đồng
⇒Ta có phương trình:0,80x*2+0,85y=362000(I)
Nếu mua trong khung giờ vàng thì món hàng A được giảm giá 30% so với giá niêm yết hay 0,70x
Nếu mua trong khung giờ vàng thì món hàng B được giảm giá 25% so với giá niêm yết hay 0,75y
Một khách hàng mua ba món hàng A và hai món hàng B trong khung giờ vàng nên phải trả số tiền là 552000 đồng
⇒Ta có phương trình:0,70x*3+0,75y*2=552000(II)
Từ (I) và (II) , ta có hệ phương trình:
{0,8x*2+0,85y=362000
{0,7x*3+0,75y*2=552000
{1,6x+0,85y=362000(1)
{2,1x+1,5y=552000(2)
Nhân cả hai vế của phương trình (1) cho 1,5, ta có:2,4x+1,275=543000(3)
Nhân cả hai vế của phương trình (2) cho 1,85,ta có:1,785x+1,275=469200(4)
Trừ từng vế của phương trình (3) cho phương trình (4), ta được:
0,615x=73800
x=120000(tmđk)
Thay x=120000 vào phương trình (2), ta được:
2,1*120000+1,5y=552000
252000+1,5y=552000
1,5y=552000-252000
1,5y=300000
y=200000
Vậy mặt hàng A có giá tiền là 120000 đồng và mặt hàng B có giá tiền là 200000 đồng