Để chứng minh phân số tối giản, ta chứng minh ƯCLN của tử số và mẫu số là \(1\).

Goi ƯCLN \(\left(\right. n - 1 ; n - 2 \left.\right) = d \Rightarrow n - 1 : d\) và \(n - 2 : d\) 

\(\Rightarrow \left(\right. n - 1 \left.\right) - \left(\right. n - 2 \left.\right) : d \Rightarrow 1 : d\)

\(\Rightarrow d = 1\) với mọi \(n\).

Vậy với mọi \(n \in \mathbb{Z}\) thì \(M = \frac{n - 1}{n - 2}\) là phân số tối giản.

1. Trong hình vẽ có 4 bộ ba điểm thẳng là: 

+) \(A , C , D\)

+) \(A , B , E\)

+) \(C , E , F\)

+) \(D , E , B\)

2.

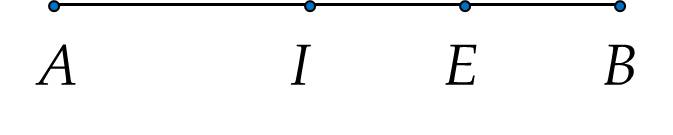
a) Theo hình vẽ, ta có: \(A I + I B = A B\)

Hay \(4 + I B = 9\)

\(I B = 9 - 4 = 5\) cm

b) Vì \(E\) là trung điểm của \(I B\) nên

\(E I = E B = \frac{I B}{2} = \frac{5}{2} = 2 , 5\) (cm)

Theo hình vẽ, ta có: \(A E = A I + I E = 4 + 2 , 5 = 6 , 5\) (cm)

Chiều dài đám đất là:

\(60. \frac{4}{3} = 80\) (m)

Diện tích đám đất là:

\(60.80 = 4 800\) (m\(^{2}\))

Diện tích trồng cây là:

\(4 800. \frac{7}{12} = 2 800\) (m\(^{2}\))

Diện tích còn lại là:

\(4 800 - 2 800 = 2 000\) (m\(^{2}\))

Diện tích ao cá:

\(2 000.30 \% = 600\) (m\(^{2}\))

a) \(\frac{- 5}{9} + \frac{8}{15} + \frac{- 2}{11} + \frac{4}{- 9} + \frac{7}{15} = \left(\right. \frac{- 5}{9} + \frac{- 4}{9} \left.\right) + \left(\right. \frac{8}{15} + \frac{7}{15} \left.\right) + \frac{- 2}{11}\)

\(= \frac{- 9}{9} + \frac{15}{15} + \frac{- 2}{11}\)

\(= - 1 + 1 + \frac{- 2}{11}\)

\(= 0 + \frac{- 2}{11} = \frac{- 2}{11}\).

b) \(\left(\right. \frac{7}{2} . \frac{5}{6} \left.\right) + \left(\right. \frac{7}{6} : \frac{2}{7} \left.\right)\)

\(= \left(\right. \frac{7}{2} . \frac{5}{6} \left.\right) + \left(\right. \frac{7}{6} . \frac{7}{2} \left.\right)\)

\(= \frac{7}{2} . \left(\right. \frac{5}{6} + \frac{7}{6} \left.\right)\)

\(= \frac{7}{2} . 2\)

\(= 7\)

a) Có \(\frac{- 3}{8} = \frac{- 9}{24} ; \frac{5}{- 12} = \frac{- 10}{12}\)

Vì \(\frac{- 9}{24} > \frac{- 10}{24}\) nên \(\frac{- 3}{8} > \frac{5}{- 12}\).

b) Có \(\frac{3131}{5252} = \frac{3131 : 101}{5252 : 101} = \frac{31}{52}\).

Vậy \(\frac{3131}{5252} = \frac{31}{52}\).

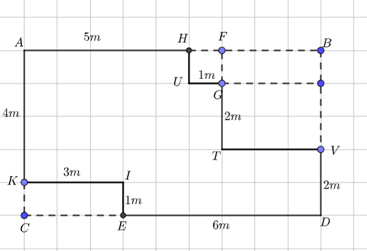
Gọi $S$ là diện tích mảnh vườn.

$S^{ABDC}=S^{KIEC}+S^{HFGU}+S^{FBVT}+S$

Suy ra $S=S^{ABDC}-S^{KIEC}-S^{HFGU}-S^{FBVT}$

$S=9.5-3.1-1.1-3.3=32$ (m${}^2$).

Gọi $a$ là số học sinh cần tìm, $a$ là số tự nhiên.

Ta có: $a⋮2$; $a⋮3$; $a⋮5$ và $430\le a\le 460$

Suy ra $a\in$ BC$(2;3;5)$ và $430\le a\le 460$

BCNN$(2;3;5)=\mathrm{2.3.5}=30$

BC$(2;3;5)=$ B$(30)=\{0;30;60;\dots ;300;330;360;390;420;450;480;\dots \}$

Vì $430\le a\le 460$ nên $a=450$.

Vậy số học sinh cần tìm là $450$ học sinh.

a) Bốn cạnh bằng nhau: EF = FG = GH = HE;

Hai cặp cạnh đối EF và GH, GF và EH song song với nhau;

Bốn đỉnh E, F, G, H.

Hai đường chéo EG, HF vuông góc với nhau

b)

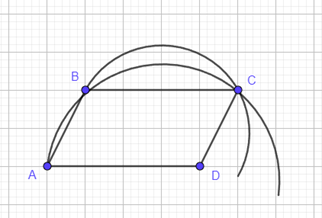
a) Ba cạnh bằng nhau: AB = BC = CA;

Ba góc ở các đỉnh A, B, C bằng nhau.

b) HS vẽ đúng hình.

a) $76.12+24.12-200$

$=12.(76+24)-200$

$=12.100-200$

$=1200-200=1000$.

b) $3^4.36+4^3.81-100$

$=81.36+64.81-100$

$=81.(36+64)-100$

$=81.100-100$

$=8100-100=8000$.