

NGUYỄN TUẤN MINH
Giới thiệu về bản thân



































Câu 1:
Bài thơ được vết thẹo thể thơ bốn chữ
Câu 2:
Đối tượng miêu tả thể hiện văn học trào phúng là: những thứ không trọn vẹn
Câu 3:
Thái độ của tác giả là cung chẳng gầy chẳng béo chỉ làng nhàng
Câu 4:
Hai câu thơ sử dụng nghẹ thuật trào phúng,tạo nên tiếng cười châm biếm,phê phán những người chơi cờ bạc chỉ biết đến lợi ích của cá nhân mà không lên quan đến hậu quả
Câu 5:
Hai câu thơ thể hiện sự chán nản thất vọng của tác giả khi nhìn lại cuộc đời mình
Câu 6:
Thông điệp của bài thơ là:
Hiểu rõ nội dung và thông điệp của bài thơ. Liên hệ với thực tế và đưa ra những việc làm cụ thể.Biểu đạt ý kiến một cách rõ ràng,mạch lạc.
Trong đời sống lối sống của em về lối sống vô trách nhiệm là do ảnh hưởng đến môi trường xã hội .Lối sống vô trách nhiệm của một bộ phận giới trẻ ngày nay là là một vấn đề đáng báo động,không quan tâm đến việc học hành ,học tập rèn luyện bản thân.Do thiếu hụt về kiến thức,kỹ năng sống ,ảnh hưởng đến bản thân là mất đi cơ phát trển và dễ bị sa ngã vào tệ nạn xã hội về lối sống vô trách nhiệm . Bài học cần phải nâng cao ý thức trách nhiệm của bản thân mình,cần rèn luyện đạo Đức lối sống,cần học hỏi kiến thức kỹ năng sống cần có sự giáo dục của gia đình và nhà trường
a. Xác định đúng yêu cầu của đề: Viết bài văn phân tích một bài thơ trào phúng.
b. Xác định đúng vấn đề: Nghị luận văn học.
c. Đề xuất được hệ thống ý làm rõ vấn đề bài viết:
– Mở bài: Giới thiệu về tác giả và bài thơ.
– Thân bài: Phân tích nội dung trào phúng của bài thơ để làm rõ chủ đề.
+ “Không học mà sao cũng gọi đồ?”: Câu hỏi tu từ thể hiện thái độ chế giễu, xem thường kẻ không học nhưng được mọi người tôn vinh, gọi là thầy đồ vì bỏ tiền ra mua danh. Câu thơ còn cho thấy đạo học, chuyện thi cử như một trò đùa.
+ “Áo quần đĩnh đạc trông ra cậu,/ Ăn nói nhề nhàng nhác giọng Ngô.”: Sự đối lập giữa hình thức bên ngoài và cốt cách bên trong tạo nên sự nhố nhăng, kệch cỡm.
+ Cách gọi “thằng” trong câu “Hỏi mãi mới ra thằng bán sắt”: Tỏ rõ thái độ mỉa mai một kẻ bán sắt không xứng để mang cái danh thầy đồ.
– Kết bài: Khẳng định giá trị, ý nghĩa của bài thơ.
d. Chính tả, ngữ pháp: Đảm bảo chuẩn chính tả, ngữ pháp tiếng Việt.
e. Sáng tạo: Sử dụng hình ảnh, từ ngữ, biện pháp tu từ độc đáo; lời văn trau chuốt, sinh động, gợi cảm.
Học sinh kể về những việc mình đã làm và sẽ làm để thể hiện tinh thần yêu nước.
– Ví dụ:
+ Bảo vệ cảnh quan thiên nhiên, giữ gìn những nét đẹp văn hóa truyền thống.
+ Học tập, noi theo tấm gương của những anh hùng, của Bác Hồ vĩ đại.
Bài thơ gửi gắm thông điệp về nỗi đau mất nước,cảnh đời lầm than của người dân trong chiến tranh,đồng thời thể hiện lòng yêu nước,căn thù giặc sâu sắc của tác giả.
a) Diện tích đáy hình vuông của chiếc lều là:
(m)
Thể tích không khí bên trong chiếc lều là:
(m).
b) Diện tích xung quanh của chiếc lều là:
(m)
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
(m).
Do nên số tiền mua vải được giảm giá trên tổng hóa đơn.
Vậy số tiền mua vải là:
(đồng).
a) Số đo góc ở đuôi chiếc diều là:
b) Xét vuông tại , theo định lí Pythagore ta có:
Xét vuông tại theo định lí Pythagore ta có:
Do đó (cm).
Suy ra (cm).
a)
b)
Từ suy ra
.
Tương tự ta có: và .
Do đó .
Vậy .
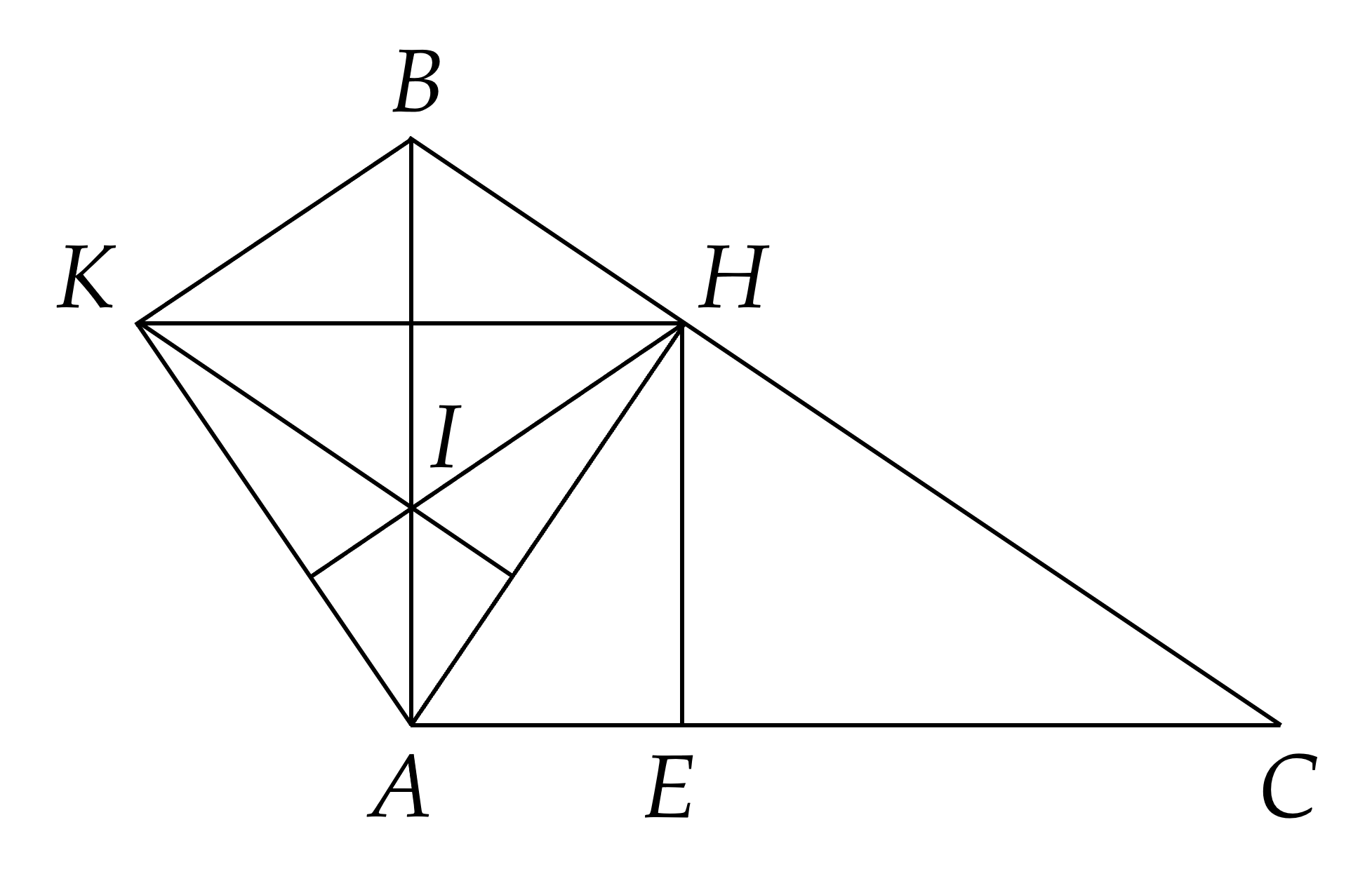
a) vuông tại suy ra suy ra .
Do suy ra ; suy ra .
Tứ giác có suy ra tứ giác là hình chữ nhật.
b) Do vuông tại , áp dụng định lí Pythagore suy ra:
nên cm.
Do là hình chữ nhật suy ra (cm).