

ĐOÀN PHAN ANH
Giới thiệu về bản thân



































Phân tích bài thơ bánh trôi nước của hồ Xuân Hương chắc cô tại Việt Nam bánh trôi nước của hồ Xuân Hương là một tác phẩm độc đáo,thể hiện tài năng và tư tưởng sĩ tài hoa. bài thơ ngắn gọn súc tích nhưng ẩn chứa nhiều tầng Ý nghĩa sâu sắc phản ánh số phận bị thương của người phụ nữ trong xã hội phong kiến.
Hình ảnh của bài thơ là chiếc bánh trôi nước, Với nét tả thực:' trắng 'màu sắc của sự trong trắng thuần khiết , tròn nhưng tượng trưng nhẹ nhàng Cho sự đầy đặn viên mãn bông bềnh chiếc bánh trôi nước được ví như người phụ nữ, Với vẻ đẹp ngoại hình thành tạo, nhưng ẩn chứa bên trong là tâm hồn, số lượng long đong,bấp bênh
Bài thơ ông đồ bốn ở phố hàng sắt là một tác phẩm ngắn gọn nhưng đầy ý nghĩa bài thơ sử dụng thơ lục bát và ngôn ngữ bình dị, tạo một bức tranh sinh động của người sống thời xưa tác giả sử dụng câu hỏi tu từ để thu hút người đọc tò mò hỏi thăm quê quán ở nơi mô Gợi lên sự tò mò sấp thân của ông đồ bốn câu hỏi không đọc mà sao vẫn gọi đồ Lại ẩn chứa những mơ của ông đồ Qua tết cô hoài là tác giả thể hiện sự khéo léo mỉa mai Châm biếm với những người không có học mà vẫn tỏ ra thông minh giỏi giang.
Em luôn tự hào về đất nước Việt Nam ,em sẽ luôn học tập thật tốt và chăm chỉ để góp phần xây dựng đất nước. Em sẽ tích cực tham gia hoạt động xã hội giúp đỡ những người khó khăn,góp phần xây dựng xã hội tốt đẹp hơn. Bên cạnh em sẽ luôn phát huy truyền thống văn hóa của dân tộc, Góp phần giữ gìn bản sắc văn hóa Việt Nam. Em tin rằng ,mỗi con đường Việt Nam đều góp phần xây dựng và đất nước ngày càng giàu đẹp.
Bài thơ gửi gắn thông điệp về nỗi đau mất nước,cảnh đời lầm than của người dân trong chiến tranh,đồng thời cũng thể hiện lòng yêu nước,căm thù giặc sâu sắc của tác giả
Một thứ vũ khí đó là khi một người vừa cầm vừa nói đến nụ cười nhăn nhở giả tạo một nụ cười thực sự là một nụ cười ấm lòng người phải xuất phát tận đáy lòng.Nó phải thể hiện sự quan tâm,mong muốn tìm hiểu về người đố diện
Từ thiếu phụ trong câu văn là
từ thiếu phụ đuợc sử dụng miêu tả một người trẻ tuổi và một chú mèo con và một đứa bé đội chín đến mười tháng tuổi
Trong đời sống lối sống của em về lối sống vô trách nhiệm là do ảnh hưởng đến môi trường xã hội .Lối sống vô trách nhiệm của một bộ phận giới trẻ ngày nay là là một vấn đề đáng báo động,không quan tâm đến việc học hành ,học tập rèn luyện bản thân.Do thiếu hụt về kiến thức,kỹ năng sống ,ảnh hưởng đến bản thân là mất đi cơ phát trển và dễ bị sa ngã vào tệ nạn xã hội về lối sống vô trách nhiệm . Bài học cần phải nâng cao ý thức trách nhiệm của bản thân mình,cần rèn luyện đạo Đức lối sống,cần học hỏi kiến thức kỹ năng sống cần có sự giáo dục của gia đình và nhà trường.
Câu 1
bài thơ được vết thẹo thể thơ bốn chữ Câu 2
Đối tượng miêu tả thể hiện văn học trào phúng là: những thứ không trọn vẹn
Câu 3
Thái độ của tác giả là cung chẳng gầy chẳng béo chỉ làng nhàng
Câu 4
Hai câu thơ sử dụng nghẹ thuật trào phúng,tạo nên tiếng cười châm biếm,phê phán những người chơi cờ bạc chỉ biết đến lợi ích của cá nhân mà không lên quan đến hậu quả
câu 5
Hai câu thơ thể hiện sự chán nản thất vọng của tác giả khi nhìn lại cuộc đời mình
câu 6
Thông điệp của bài thơ là
hiểu rõ nội dung và thông điệp của bài thơ. Liên hệ với thực tế và đưa ra những việc làm cụ thể.Biểu đạt ý kiến một cách rõ ràng,mạch lạc
Từ x+y+z=0 suy ra x+y=−z
x2+2xy+y2=z2
x2+y2−z2=−2xy.
Tương tự ta có: y2+z2−x2=−2yz và z2+x2−y2=−2zx.
Do đó A=xy−2xy+yz−2yz+zx−2zx=−12−12−12=−32.
Vậy A=−32.
a) ΔABC vuông tại A suy ra BAC^=90∘ suy ra DAE^=90∘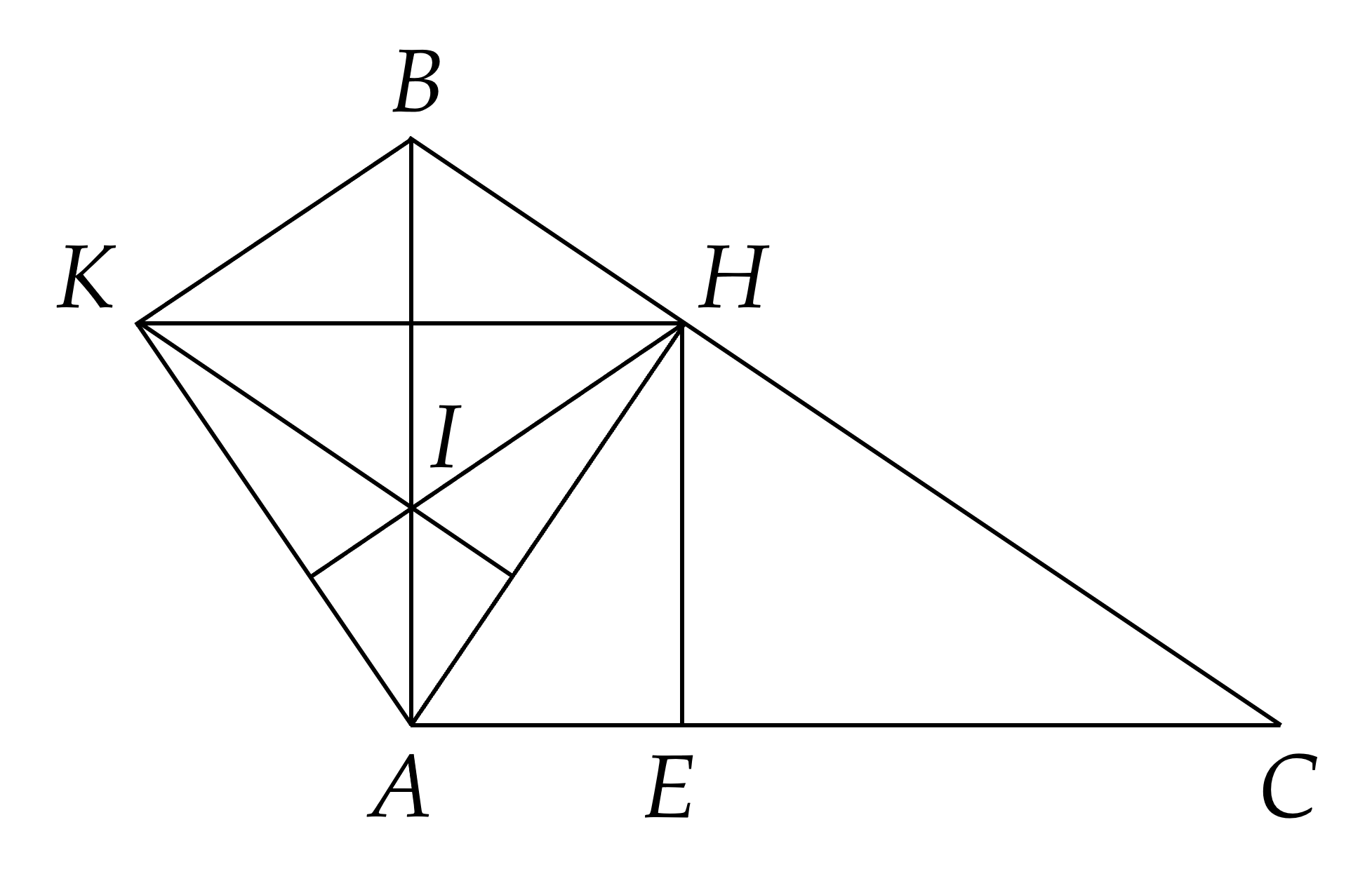
.
Do HD⊥AB suy ra HDA^=90∘
; HE⊥AC suy ra HEA^=90∘
.
Tứ giác ADHE có DAE^=HDA^=HEA^=90∘
suy ra tứ giác ADHE là hình chữ nhật.
b) Do ΔAHD vuông tại D, áp dụng định lí Pythagore suy ra:
AH2=AD2+DH2
25=16+DH2
DH2=9 nên DH=3 cm.
Do ADHE là hình chữ nhật suy ra SADHE=AD.DH=4.3=12 (cm2).