

BÙI HỒNG QUÂN
Giới thiệu về bản thân



































Vẽ biểu đồ đoạn thẳng.
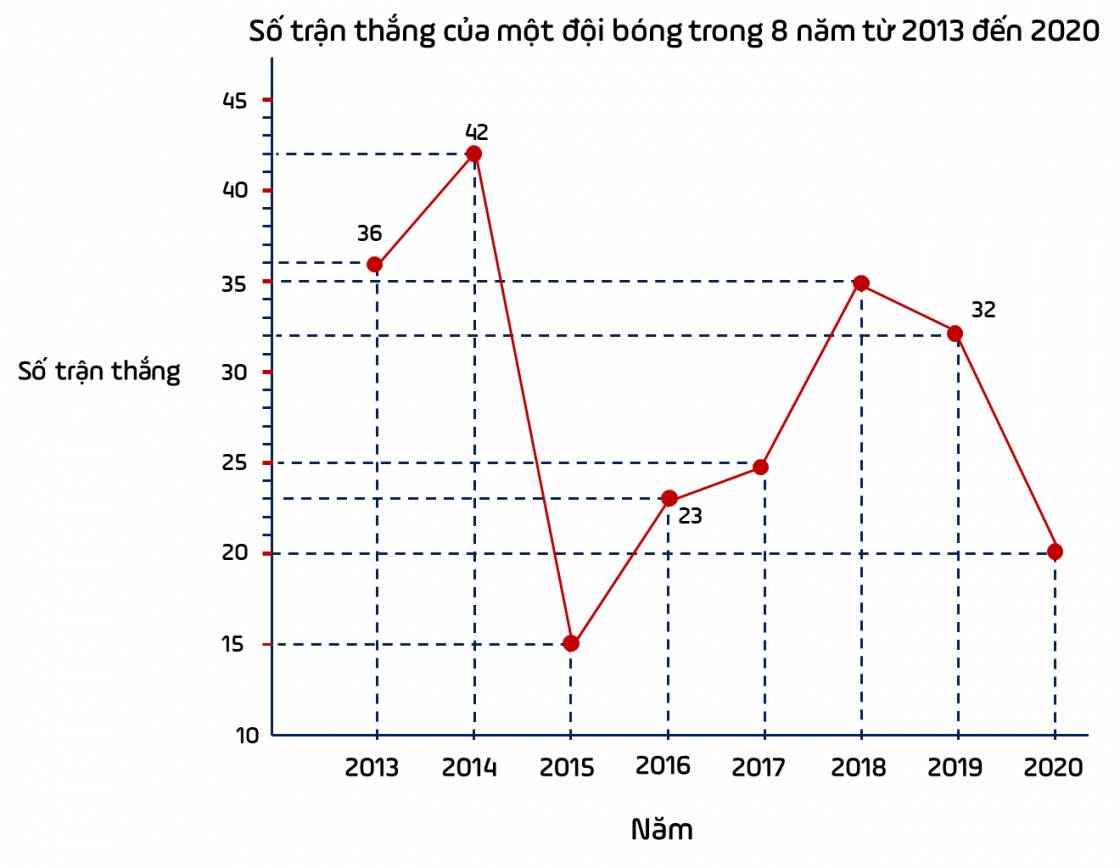
- Nhận xét: Từ năm 2015 đến năm 2018, số trận thắng của đội bóng có xu hướng tăng.
Vẽ biểu đồ đoạn thẳng
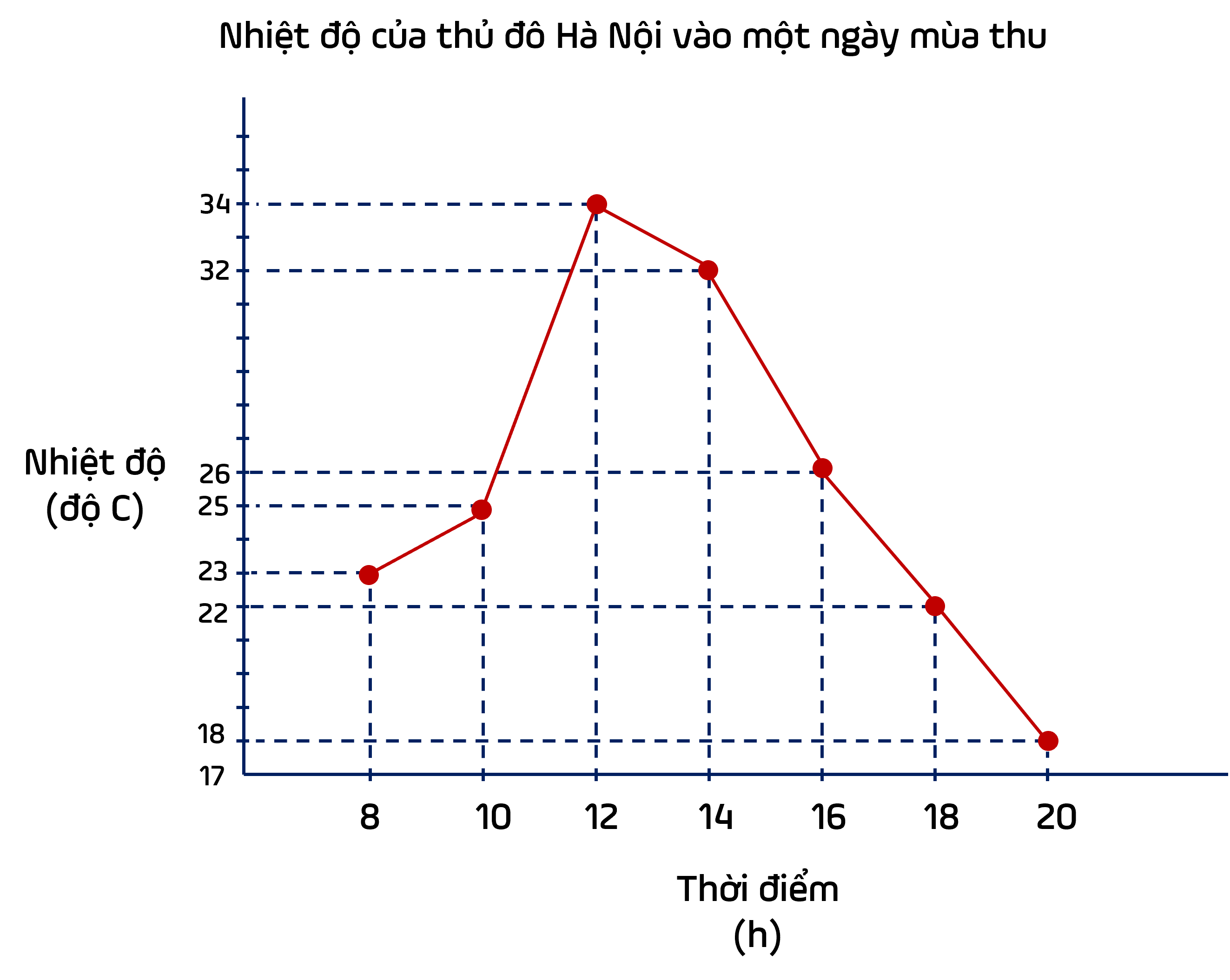
Lưu ý: Trục đứng (thành tích) không nhất thiết phải bắt đầu từ 0.
- Để nhận xét biểu đồ đoạn thẳng, ta nhận xét xu hướng của biểu đồ.
Từ tuần 1 đến tuần 3, biểu đồ nằm ngang, nên trong thời gian này, thành tích của cận động viên giữ nguyên là 8 phút.
Từ tuần 3 đến tuần 5, biểu đồ có xu hướng đg thi xuống, nên trong thời gian này, thành tích của cận động viên đã được cải thiện từ 8 phút xuống đến 6,5 phút (chạy nhanh hơn nên thời gian giảm).
Từ tuần 5 đến tuần 6, biểu đồ nằm ngang, nên tronời gian này, thành tích của cận động viên giữ nguyên là 6,5 phút.
Từ tuần 6 đến tuần 7, thành tích của vận động viên được cải thiện từ 6,5 phút xuống 6 phút.
+ Giả sử
Khi đó
Tương tự và .
Theo đề bài suy ra .
Mà nên , và cùng âm hoặc cùng dương, do đó .
+ Với :
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
Từ đây, suy ra
Vậy .
+ Giả sử
Khi đó
Tương tự và .
Theo đề bài suy ra .
Mà nên , và cùng âm hoặc cùng dương, do đó .
+ Với :
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
Từ đây, suy ra
Vậy .
a) Vì nên (1).
Mặc khác, (2).
Từ (1) và (2) suy ra .
b) (cặp góc so le trong).
Mặt khác,
Thay số:
(hai góc so le trong).
a)
b)
Áp dụng tính chất tỉ lệ thức, ta có:
hoặc
Vậy hoặc
a)
b)
Áp dụng tính chất tỉ lệ thức, ta có:
hoặc
Vậy hoặc
a)
b)
c)
a)
b) ;
hoặc
hoặc
c) .
Áp dụng tính chất tỉ lệ thức, ta được:
hoặc
hoặc