

Hoàng Trần Bảo Ngọc
Giới thiệu về bản thân



































a)
MAB
Vì điểm MM là trung điểm của đoạn thẳng ABAB.
Suy ra $AM=MB=\dfrac{AB}2=\dfrac 42=2 (cm).
b)
![]() Trường hợp 1.
Trường hợp 1.
MABxy
xMy^=60∘xMy=60∘.
![]() Trường hợp 2.
Trường hợp 2.
MABxy
xMy^=160∘xMy=160∘.
Số học sinh giỏi của lớp 6A là:
720⋅40=14207⋅40=14 (học sinh)
Số học sinh trung bình của lớp 6A là:
18⋅40=581⋅40=5 (học sinh)
Số học sinh khá của lớp 6A là:
14+5=1914+5=19 (học sinh)
Số học sinh yếu của lớp 6A là:
40−(14+5+19)=240−(14+5+19)=2 (học sinh) .
a) 12⋅43−203⋅4521⋅34−320⋅54
=23−163=32−316
=−143=−314 ;
b) 37+−619+47+−131973+19−6+74+19−13
=(37+47)+(−619+−1319)=(73+74)+(19−6+19−13)
=77+−1919=77+19−19
=1+(−1)=0=1+(−1)=0 ;
c) 35⋅89−79⋅35+35⋅26953⋅98−97⋅53+53⋅926
=35⋅(89−79+269)=53⋅(98−97+926)
=35⋅279=53⋅927
=35⋅3=53⋅3
=95=59.
Goi ƯCLN (n−1;n−2)=d⇒n−1:d(n−1;n−2)=d⇒n−1:d và n−2:dn−2:d
⇒(n−1)−(n−2):d⇒1:d⇒(n−1)−(n−2):d⇒1:d
⇒d=1⇒d=1 với mọi nn.
Vậy với mọi n∈Zn∈Z thì M=n−1n−2M=n−2n−1 là phân số tối giản.
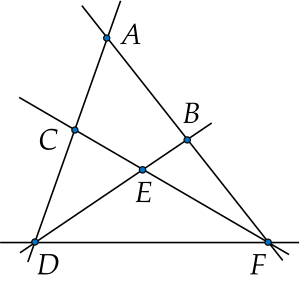
1. Cho hình vẽ sau. Kể tên các bộ 3 điểm thẳng hàng.
2. Vẽ đoạn thẳng AB=9AB=9 cm. Điểm II nằm giữa AA và BB sao cho AI=4AI=4 cm.
a) Tính độ dài đoạn thẳng IBIB.
b) Gọi EE là trung điểm đoạn thẳng IBIB. Tính độ dài đoạn thẳng AEAE.
Hướng dẫn giải:
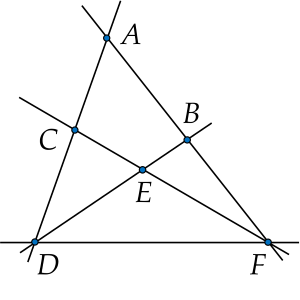
1. Trong hình vẽ có 4 bộ ba điểm thẳng là:
+) A,C,DA,C,D
+) A,B,EA,B,E
+) C,E,FC,E,F
+) D,E,BD,E,B
2.
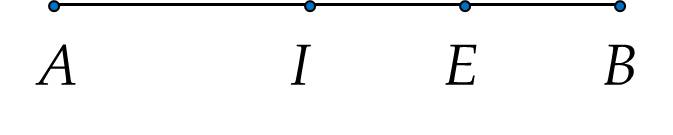
a) Theo hình vẽ, ta có: AI+IB=ABAI+IB=AB
Hay 4+IB=94+IB=9
IB=9−4=5IB=9−4=5 cm
b) Vì EE là trung điểm của IBIB nên
EI=EB=IB2=52=2,5EI=EB=2IB=25=2,5 (cm)
Theo hình vẽ, ta có: AE=AI+IE=4+2,5=6,5AE=AI+IE=4+2,5=6,5 (cm)
600mét vuông
= 7
a) Có −38=−924;5−12=−10128−3=24−9;−125=12−10
Vì −924>−102424−9>24−10 nên −38>5−128−3>−125.
b) Có 31315252=3131:1015252:101=315252523131=5252:1013131:101=5231.
Vậy 31315252=315252523131=5231.