1. No, I don't

2. I play word puzzles

3. It's blue

4. My hobby is badminton

1. My father name's Dai

2. My hobbies are travelling, cooking, dancing, and singing

3. Yes, I can

4. My father name's Dai

5. Her hobby is cooking

1. That's an eye

2. She's three years old

3. Her hobby is cooking

4. His hobby is running

5. No, it isn't. It's Ben

1. My name's Mai

2. I'm thirty years old

3. My hobbies are shopping, travelling, cooking and dancing

4. Her hobby is cooking

1. It's an ear

2. She's 6 years old

3. Yes, it is

4. It's singing

a) + Theo quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$
Suy ra $|\overrightarrow{AB}+\overrightarrow{AD}|=|\overrightarrow{AC}|=AC$.
Áp dụng định lí Pitago ta có
$$
A C^{2}=A B^{2}+B C^{2}=2 a^{2} \Rightarrow A C=\sqrt{2} a
$$
Vậy $|\overrightarrow{AB}+\overrightarrow{AD}|=a\sqrt{2}$
+ Vì O là tâm của hình vuông nên $\overrightarrow{OA}=\overrightarrow{CO}$ suy ra
$$
\overrightarrow{O A}-\overrightarrow{C B}=\overrightarrow{C O}-\overrightarrow{C B}=\overrightarrow{B C}
$$
Vậy $|\overrightarrow{OA}-\overrightarrow{CB}|=|\overrightarrow{BC}|=a$
+ Do $ABCD$ là hình vuông nên $\overrightarrow{CD}=\overrightarrow{BA}$ suy ra $\overrightarrow{CD}-\overrightarrow{DA}=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}$ Mà $|\overrightarrow{BD}|=BD=\sqrt{A{B}^2+A{D}^2}=a\sqrt{2}$ suy ra $|\overrightarrow{CD}-\overrightarrow{DA}|=a\sqrt{2}$

Theo quy tắc ba điểm ta có
- $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
Mà $\sin \widehat{ABC}=\genfrac{}{}{0ex}{}{AC}{BC}$
$\Rightarrow AC=BC\cdot \sin \widehat{ABC}=a\sqrt{5}\cdot \sin 30^{\circ }=\genfrac{}{}{0ex}{}{a\sqrt{5}}{2}$
Do đó $|\overrightarrow{AB}+\overrightarrow{BC}|=|\overrightarrow{AC}|=AC=\genfrac{}{}{0ex}{}{a\sqrt{5}}{2}$
- $\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$
Ta có $A{C}^2+A{B}^2=B{C}^2\Rightarrow AB=\sqrt{B{C}^2-A{C}^2}=\sqrt{5a^2-\genfrac{}{}{0ex}{}{5a^2}{4}}=\genfrac{}{}{0ex}{}{a\sqrt{15}}{2}$
Vì vậy $|\overrightarrow{AC}-\overrightarrow{BC}|=|\overrightarrow{AB}|=AB=\genfrac{}{}{0ex}{}{a\sqrt{15}}{2}$
- Gọi $D$ là điểm sao cho tứ giác $ABDC$ là hình bình hành.
Khi đó theo quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$
Vì tam giác $ABC$ vuông ở $A$ nên tứ giác $ABDC$ là hình chữ nhật suy ra $AD=BC=a\sqrt{5}$
Vậy $|\overrightarrow{AB}+\overrightarrow{AC}|=|\overrightarrow{AD}|=AD=a\sqrt{5}$.

Giả sữ: $\vec{a}=\overrightarrow{AB}$ và $\vec{b}=\overrightarrow{BC}$ thì $\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
a) Nếu $\vec{a}$ và $\vec{b}$ cùng hướng thì $|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|$.
Nếu $\vec{a}$ và $\vec{b}$ cùng hướng thì 3 điểm $A,B,C$ cùng thuộc một đường thẳng và $B$ nằm giừa $A,C$.

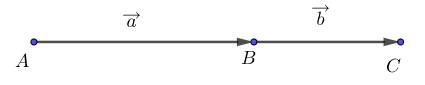
Do đó $|\vec{a}+\vec{b}|=|\overrightarrow{AB}+\overrightarrow{BC}|=|\overrightarrow{AC}|=AB+BC=|\vec{a}|+|\vec{b}|$.
Vậy $|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|$.
b) Nếu $\vec{a}$ và $\vec{b}$ ngược hướng và $|\vec{b}|\ge |\vec{a}|$ thì $|\vec{a}+\vec{b}|=|\vec{b}|-|\vec{a}|$.
Nếu $\vec{a}$ và $\vec{b}$ ngược hướng và $|\vec{b}|\ge |\vec{a}|$ thì ba điểm $A,B,C$ cùng thuộc một đường thẳng và $A$ nằm giừa $B,C$.

Do đó $|\vec{a}+\vec{b}|=|\overrightarrow{AB}+\overrightarrow{BC}|=AC=BC-AB=|\vec{b}|-|\vec{a}|$.
Vậy $|\vec{a}+\vec{b}|=|\vec{b}|-|\vec{a}|$.
c) $|\vec{a}+\vec{b}|\le |\vec{a}|+|\vec{b}|$. Khi nào xảy ra dấu đẳng thức?
Từ chứng minh ở câu a và b:
$\Rightarrow$ nếu $\vec{a}$ và $\vec{b}$ cùng phương thì $|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|$ hoặc $|\vec{a}+\vec{b}|<|\vec{a}|+|\vec{b}|$.
Nếu $\vec{a}$ và $\vec{b}$ không cùng phương thi $A,B,C$ không thẳng hàng.
Xét $△ABC$ có hệ thức $AC<AB+BC$. Do đó $|\vec{a}+\vec{b}|<|\vec{a}|+|\vec{b}|$.
Như vậy, trong mọi trường hợp ta có: $|\vec{a}+\vec{b}|\le |\vec{a}|+|\vec{b}|$, đẳng thức xảy ra khi $\vec{a}$ và $\vec{b}$ cùng hướng.

a) Vì $PN,MN$ là đường trung bình của tam giác $ABC$ nên
$PN//BM,MN//BP$ suy ra tứ giác $BMNP$ là hình bình hành
$\Rightarrow \overrightarrow{BM}=\overrightarrow{PN}$
$N$ là trung điểm của $AC\Rightarrow \overrightarrow{CN}=\overrightarrow{NA}$
Do đó theo quy tắc ba điểm ta có

a) Ta có $\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AC}$
$=-(\overrightarrow{AB}+\overrightarrow{AD})+\overrightarrow{AC}$
Theo quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ suy ra
$\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=-\overrightarrow{AC}+\overrightarrow{AC}=\overrightarrow{0}.$

b) Vì $\mathrm{ABCD}$ là hình bình hành nên ta có: $\overrightarrow{OA}=\overrightarrow{CO}\Rightarrow \overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AO}=\overrightarrow{0}$
Tương tự: $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$.
c) Cách 1: Vì $\mathrm{ABCD}$ là hình bình hành nên $\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow \overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{AB}=\overrightarrow{0}$